Introduction to Time Series
Case Study: Forecasting Housing Prices
Seminar Overview
Seminar Details
- This code file was prepared for a seminar at Duke University’s Fuqua School of Business
Intended Audience
- The audience is Masters students in Data Science
- Seminar attendees are expected to have a working knowledge of R, statistics, basic econometrics, and machine learning
- Seminar attendees are NOT expected to have any knowledge of time series analysis
Accompanying materials
Theoretical aspects of the topics discussed are relegated to a series of ``lecture notes’’ available at Prof. Aguilar’s website.
Contact Information
- aguilar-mike@outlook.com
- https://www.linkedin.com/in/mike-aguilar-econ/
Using this document
Throughout this code example, you’ll see several questions indicated by “Q”. Each question is followed by a solution, indicated by “A”.
The best way to learn this material is through active participation. I suggest that you attempt to formulate your own answers to each question before viewing the prepared “A” answer.
Case Study Background
In this case study we are attempting to forecast house price growth.
We will structure these forecasts using the natural temporal persistence in this series, as well as leveraging the information contained in exogenous drivers such as housing starts.
Outline
We will categorize our research process into 3 broad steps: 1) Explore, 2) Explain, 3) Forecast.
Package details
Several packages are used throughout this case study. Although the best practice is to invoke the library call for all packages within housekeeping, we invoke near the code implementation so that we can see when and how each package is used.
Explore
Housekeeping
Standard best practice to clear workspace:
rm(list=ls()) # clear work space
cat("\014") # clear console Data
Our object of interest is housing starts. An important feature is housing prices. There are undoubtedly many other relevant features, but we will focus on this manageable subset so that we can focus on the time series methods. The specific features are chosen to highlight certain time series techniques, not necessarily their explanatory power.
Our data source will be FRED (https://fred.stlouisfed.org/) from the St. Louis Federal Reserve.
We can obtain our data via FRED’s API using the fredr package. To do so, you need to obtain a free API key by visiting (https://fred.stlouisfed.org/docs/api/api_key.html).
After you’ve obtained the key, save it to a sample txt file and store in your working directory.
Connect to FRED API
#install.packages("fredr")
library(fredr)
fred_api_key = read.delim("API_Key.txt", header = FALSE, sep="")[[1]]
fredr_set_key(fred_api_key) #Store the API key as an environment variableDownload Housing Prices
Set start/end dates
Q: Can you define the start and end dates for Jan59 through Dec23?
A:
startdate = "1959-01-01"
enddate = "2023-12-01"Notice that the FRED database uses the first of the month as a generic placeholder for the monthly value. That is in contrast to 1) the date at which the data for that month was released, and 2) in contrast for the date at which the activity took place
Download Prices
In order to download data via FREDR we need the FRED series_id. These are easily obtained by searching directly on FRED’s website.
Price: S&P/Case-Shiller U.S. National Home Price Index (CSUSHPINSA)
CSUSHPINSA<-fredr(
series_id = "CSUSHPINSA",
frequency = "m", # monthly
observation_start = as.Date(startdate),
observation_end = as.Date(enddate)
)Download Housing Starts
Housing starts: New Privately-Owned Housing Units Started: Total Units (HOUSTNSA)
HOUSTNSA<-fredr(
series_id = "HOUSTNSA",
frequency = "m", # monthly
observation_start = as.Date(startdate),
observation_end = as.Date(enddate)
)
HOUSTNSA$value <- HOUSTNSA$value*1000 # Convert raw data "Thousands of Units" to "Units" Combine
Let’s combine the data into a single data frame for ease of analysis.
library(dplyr)
HOUSTNSA<-HOUSTNSA %>%
dplyr::select(date,value)
CSUSHPINSA<-CSUSHPINSA %>%
dplyr::select(date,value)
temp_df<-merge(HOUSTNSA,CSUSHPINSA,by="date",all=T)
colnames(temp_df) <- c("Date","HousingStart","PriceIndex")Check for missing
Q: Do we have a balanced panel?
head(temp_df) Date HousingStart PriceIndex
1 1959-01-01 96200 NA
2 1959-02-01 99000 NA
3 1959-03-01 127700 NA
4 1959-04-01 150800 NA
5 1959-05-01 152500 NA
6 1959-06-01 147800 NAA: No. We can see right away that we don’t have a balanced panel. Notice the NAs for the Price Index.
Q: How many NA’s do we have?
summary(is.na(temp_df)) Date HousingStart PriceIndex
Mode :logical Mode :logical Mode :logical
FALSE:780 FALSE:780 FALSE:444
TRUE :336 A: 336 missing from PriceIndex.
Q: When are these missing values?
idxHousingStarts<-is.na(temp_df$HousingStart)
idxPrices<-is.na(temp_df$PriceIndex)
par(mfrow=c(1,2))
plot(idxPrices,main="Prices")
plot(idxHousingStarts,main="HousingStarts")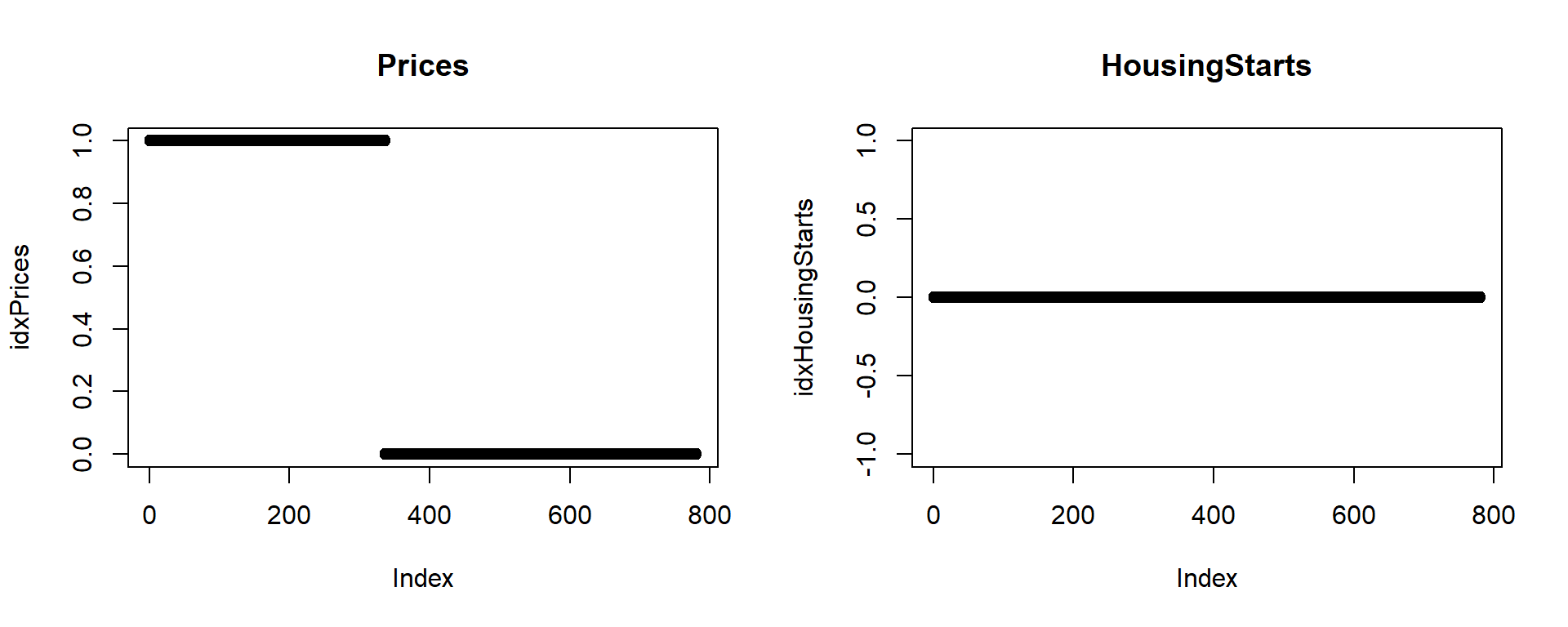
A: Importantly, the missing observations only are at the beginning and end of the series. This is a signal of something structural. e.g. The Price Index simply wasn’t constructed at the early dates.
Clean
Q: Suppose the values were missing throughout the time series (e.g. some in 1959, some in 1978, etc..)? How could we fix?
A:
We should NOT simply eliminate the rows with missing data. This (usually) works fine in cross sectional data. But in time series, each row is connected to the nearby rows. Omitting a row deletes critical information, which most likely will influence your results.
We must think WHY the data is missing. If it is random throughout the series, then we could use a local mean between adjacent points, or some other method of interpolation.
Thankfully, in our case, the data is missing at the edges of the dataset for a structural reason we noted above. So, we can trim the sample to make the series balanced.
df <- na.omit(temp_df) # remove the rows with NA
head(df) Date HousingStart PriceIndex
337 1987-01-01 105100 63.733
338 1987-02-01 102800 64.133
339 1987-03-01 141200 64.468
340 1987-04-01 159300 64.972
341 1987-05-01 158000 65.547
342 1987-06-01 162900 66.218Basic EDA
EDA in time series looks much like typical EDA, but the temporal nature does offer some differences in interpretation and other avenues to explore.
Full sample correlation matrix
cor(df[,c(-1)]) # get grid of the date column HousingStart PriceIndex
HousingStart 1.00000000 0.01091284
PriceIndex 0.01091284 1.00000000Q: Interpret the correlation. We might this not be a good measure of the relationship between these two series?
A:
- The correlation of ~.01 implies that on average the movements of housing starts over time don’t track well the movements of housing prices.
- This might not be an appropriate measure of the relationship between the series for several reasons.
- The two series might not move together contemporaneously. e.g. perhaps prices this month correlate to starts in five months from now (lead/lag).
- Also, the correlation only captures the average relationship through time. Perhaps the the series move together only in up/down trends, but not in the middle of their respective distributions.
- Or perhaps their relationships have changed through time.
- We will need more instructive EDA for time series.
Descriptive Stats
summary(df) Date HousingStart PriceIndex
Min. :1987-01-01 Min. : 31900 Min. : 63.73
1st Qu.:1996-03-24 1st Qu.: 86975 1st Qu.: 82.03
Median :2005-06-16 Median :113050 Median :141.88
Mean :2005-06-16 Mean :111370 Mean :143.07
3rd Qu.:2014-09-08 3rd Qu.:136850 3rd Qu.:180.26
Max. :2023-12-01 Max. :197900 Max. :312.94 Time Series Plots
library(tidyverse)
plot_df <- df %>%
`colnames<-`(c("Date","HousingStart","PriceIndex \n(Jan 2000=100)")) %>%
pivot_longer(c("HousingStart","PriceIndex \n(Jan 2000=100)")) # Convert wide dataframe to long
ggplot(data = plot_df, aes(x = Date,y = value, group = name, color = name)) +
geom_line() +
scale_x_date(date_labels = "%Y (%b)") + # format datetime
facet_grid(name~., scales = "free_y") +
labs(x = "", y = '') +
theme(legend.position = "none")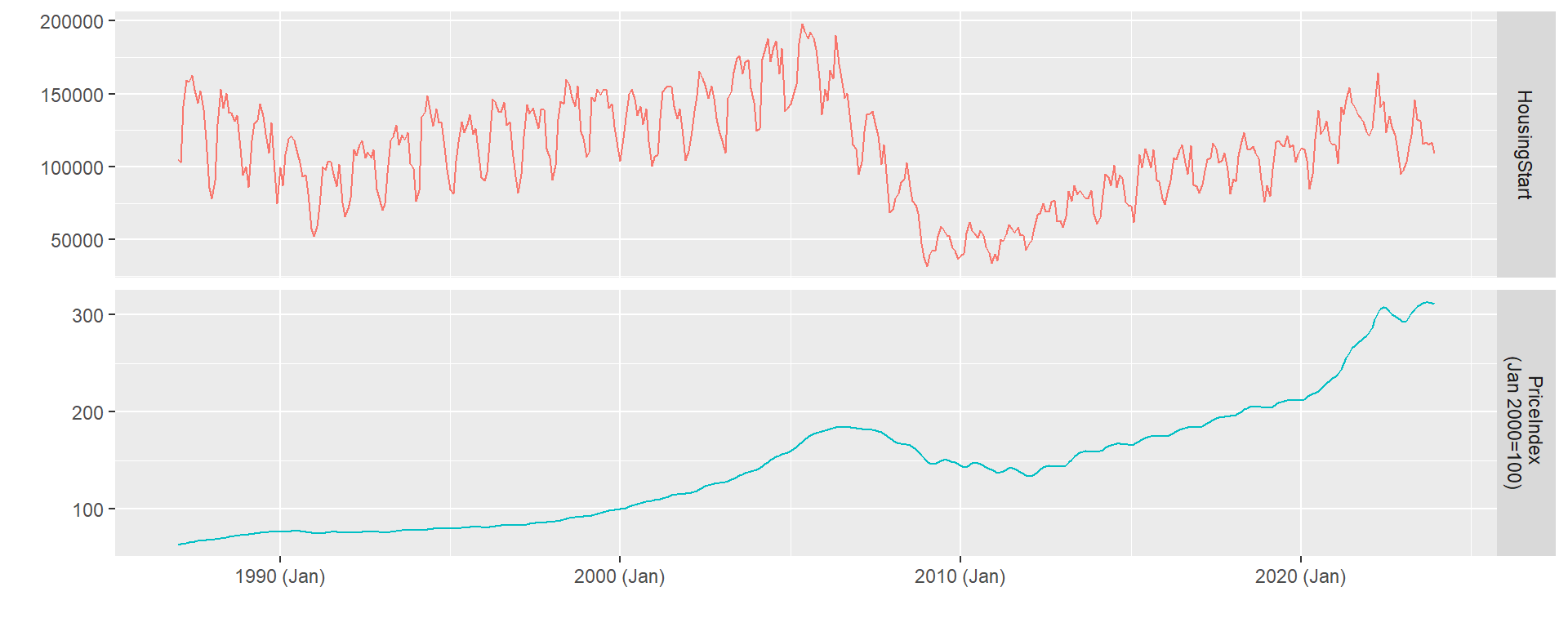
Q: What patterns/properties do you notice?
A: 1. The periodic patterns in housing starts is indicative of seasonality.
2. The trend in the price index is indicative of non stationarity.
We need to address each before we proceed with modeling.
Seasonality
Understand Seasonality
Let’s zoom in on housing starts.
library(ggplot2)
ggplot(data = df, aes(x = Date,y = HousingStart)) +
geom_line() +
scale_x_date(date_labels = "%Y (%b)") + # format datetime
labs(x = "", y = "Housing Start Units")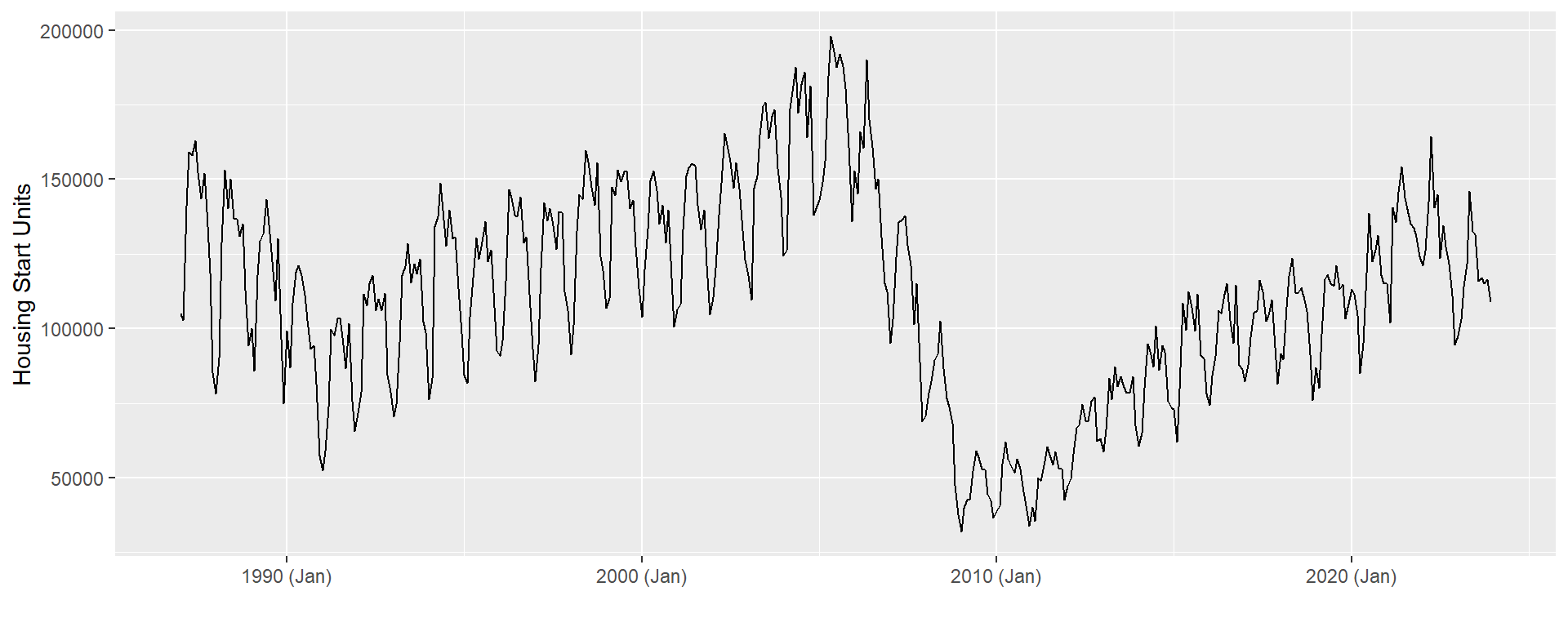
Q: Be sure to stop and think about why there is temporal persistence and why that persistence occurs in a seasonal pattern. If we can’t find an ``economic’’ reason, we may be overlooking an important feature.
Why might this seasonality exist?
A: Weather is likely the main culprit. It is easiest to build homes during clement weather. As such, housing starts often start to rise in the Spring and tend to fall in the Winter.
There are many ways to adjust for these seasonal patterns.
Prepare the df for analysis
library(xts)
FirstObs=df$Date[1]
#We could parse the FirstObs chr string, but for our purposes it's easier to input by hand the start date
df_ts <- ts(xts(df[,2:3], order.by = df$Date), frequency = 12, start = c(1987,1)) Moving Avg
Q: Can you create a 24 month simple moving average? Use the `SMA’ command. What’s the purpose?
library(TTR)
SMA24<-SMA(df_ts[,"HousingStart"],n=24) # Create a simple 24 period moving avg using `SMA()`
toplot<-cbind(as.xts(df_ts[,"HousingStart"]),as.xts(SMA24))
colnames(toplot)[1]="Level" # Add column name
colnames(toplot)[2]="24mth MovAvg" # Add column name
plot(toplot,main="Housing Starts",legend.loc="topright", auto.legend=TRUE)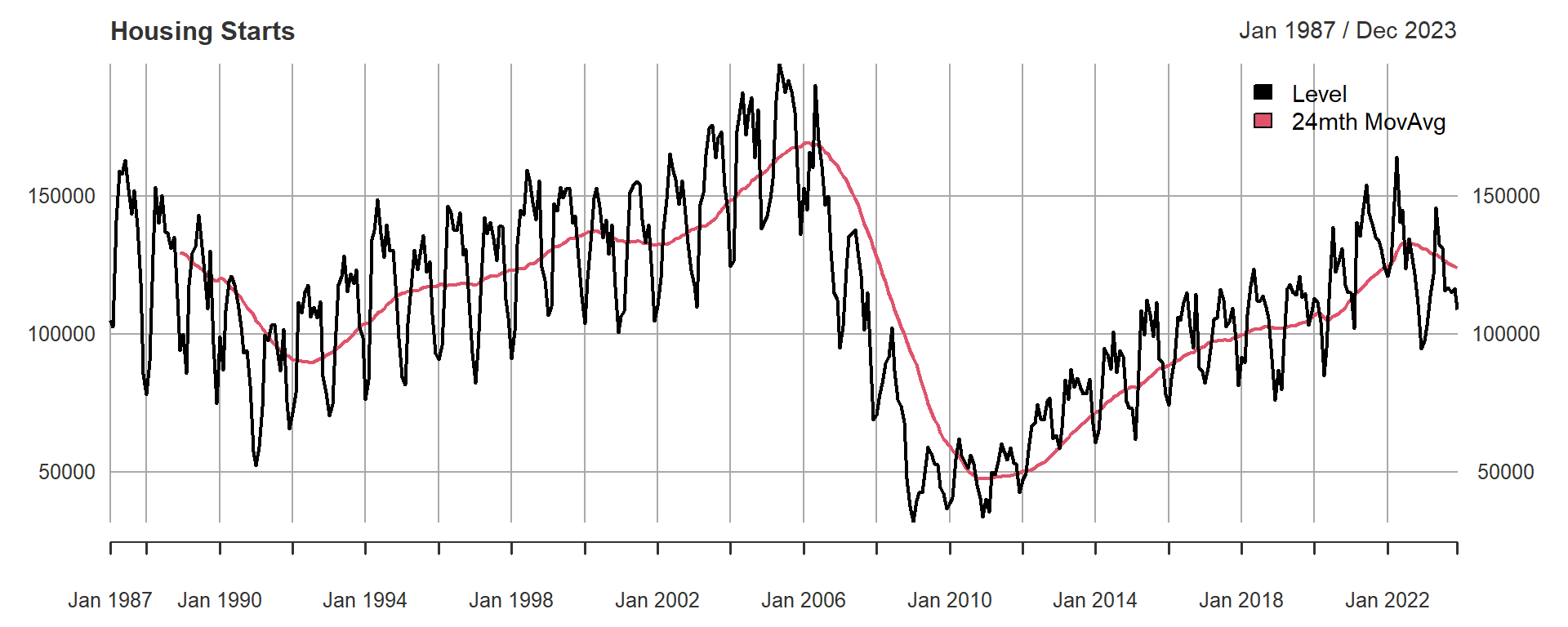
A:
- The red line (i.e. the SMA) takes the trailing local average over 24months.
- The smoother average can give us a sense of the underlying trend of housing starts, abstracting away from the seasonal variation.
- In our case, housing starts have been declining in the recent period, but not by as much as the raw series suggests, because we are in a seasonal down turn near the end of the series (Winter 2023).
Seasonal Decomposition
We could decompose the housing starts series into 3 pieces: 1) trend, 2) seasonal, 3) noise. The decomposition can be additive or multiplicative. There are numerous techniques for identifying and extracting the 3 components. Let’s demonstrate a few.
Classical Decomposition
Classical decomposition methods compute the seasonal component by essentially including dummy variables for each periodic unit (e.g. month, quarters, etc..)
library(stats)
decomp<-decompose(df_ts[,"HousingStart"], type="additive")
plot(decomp) # plot components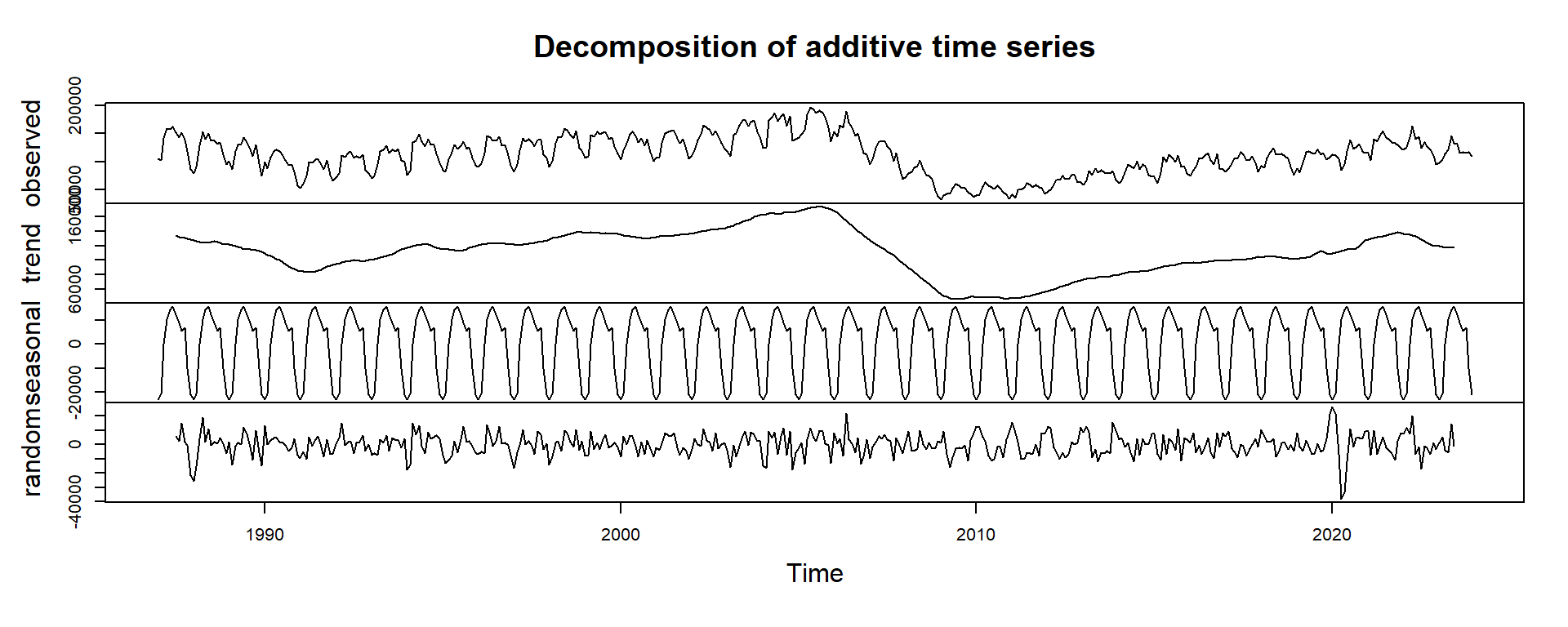
Q: Explain the 4 panels in the plot above.
A:
- Panel 1: Raw data
- Panel 2: Trend of the housing starts series, which is extracted using a moving average
- Panel 3: Seasonal captures the seasonal variations of the Raw data around the trend
- Panel 4: Is the noise in the Raw data that can not be explained by the Trend nor the Seasonal components
Q: How do we use the composition to create a seasonally adjusted value? Why might you want this series?
A:
- After the decomposition is implemented we can easily construct a seasonally adjusted series by subtracting the seasonal components from the raw series.
- We often report time series as seasonally adjusted values to abstract away from the seasonal variations and uncover the structural behavior of the time series.
- For instance, policy makers might be able to influence the underlying trend.
SA = decomp$x-decomp$seasonal # Raw Minus SeasonalCompare the SA and NSA
Trend = decomp$trend
library(forecast)
forecast::autoplot(df_ts[,"HousingStart"], series="Raw Data") +
forecast::autolayer(decomp$x-decomp$seasonal, series="Seasonally Adjusted") +
forecast::autolayer(decomp$trend, series="Trend") +
xlab("Year") + ylab("") + labs(color = "") +
ggtitle("Classical Additive Seasonally Adjusted") +
scale_colour_manual(values=c("black","blue","red"), breaks=c("Raw Data","Seasonally Adjusted","Trend")) +
theme(legend.position="bottom")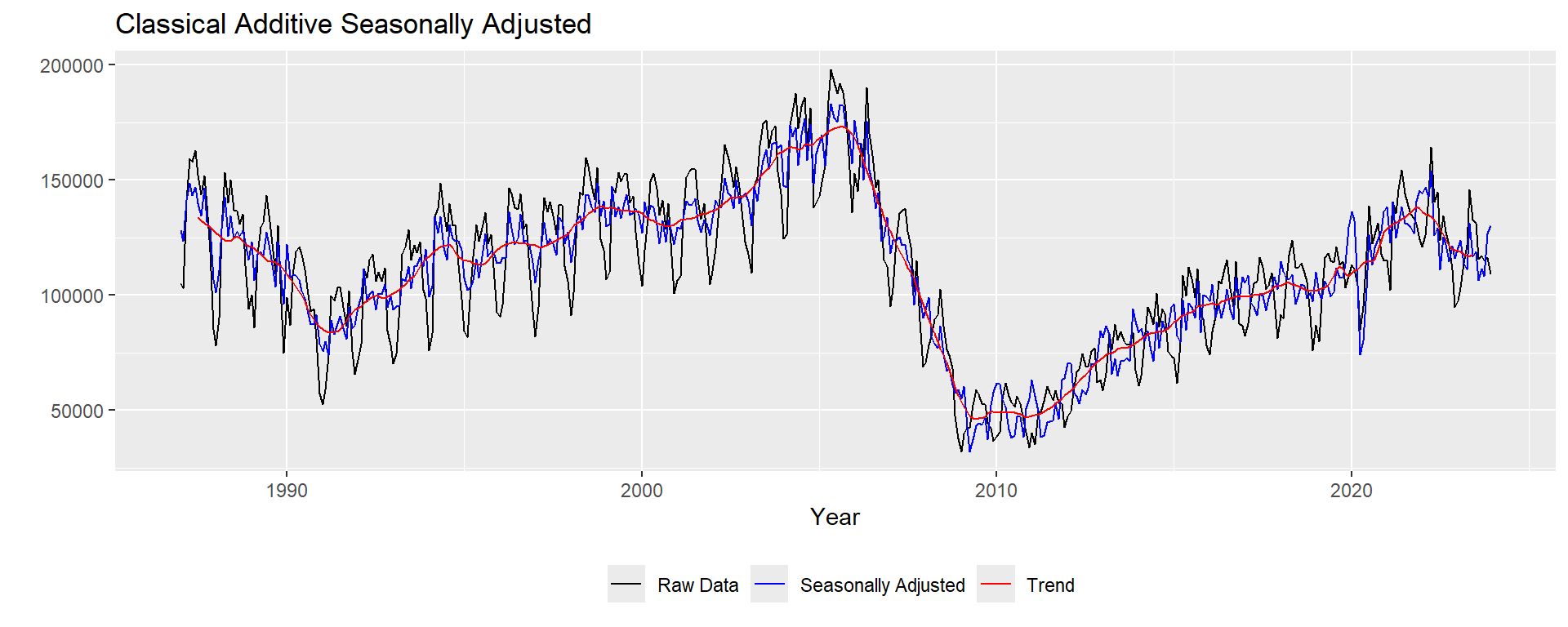
X11 Decomposition
The X11 approach is a variant of the classical decomposition.
library(seasonal)
x11decomp <- seas(df_ts[,"HousingStart"], x11="")
forecast::autoplot(x11decomp) +
ggtitle("X11 Decomposition")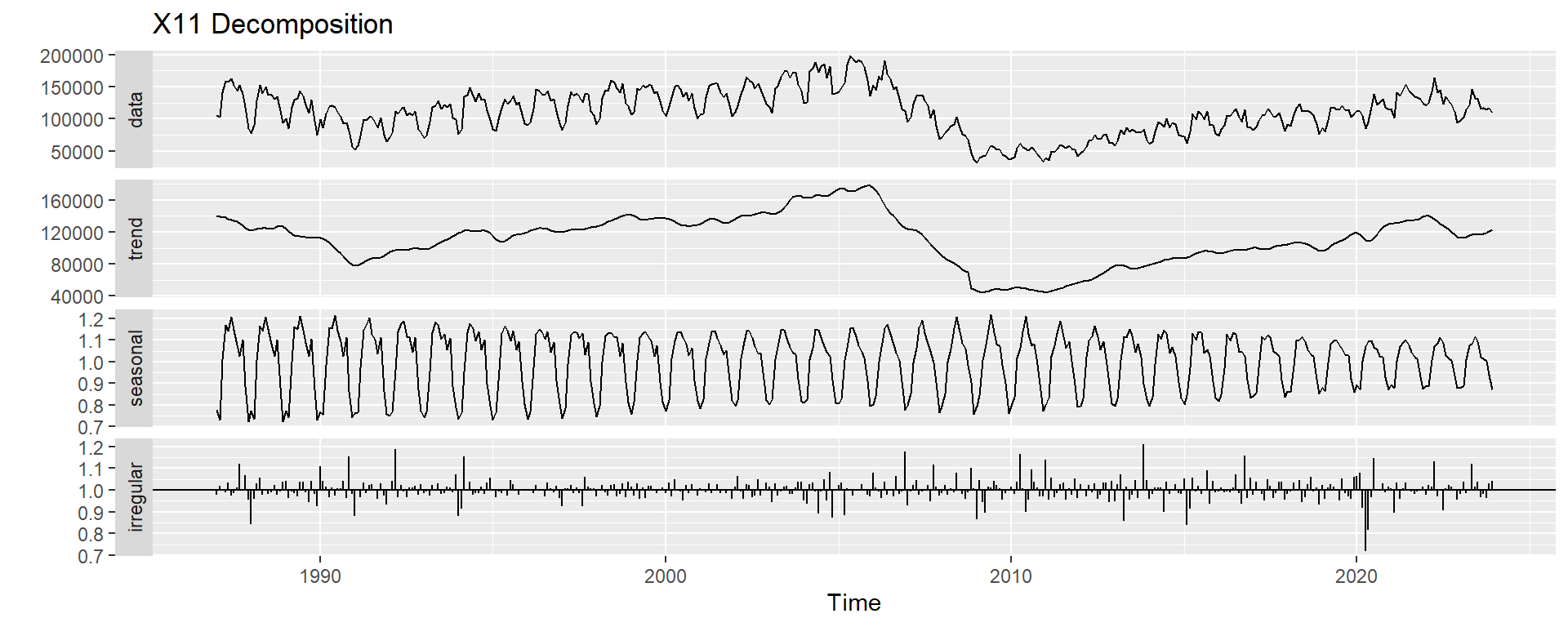
Compare SA and NSA
forecast::autoplot(df_ts[,"HousingStart"], series="Raw Data") +
autolayer(seasadj(x11decomp), series="Seasonally Adjusted") +
autolayer(trendcycle(x11decomp), series="Trend") +
xlab("Year") + ylab("") + labs(color = "") +
ggtitle("X11 Seasonally Adjusted") +
scale_colour_manual(values=c("black","blue","red"), breaks=c("Raw Data","Seasonally Adjusted","Trend")) +
theme(legend.position="bottom")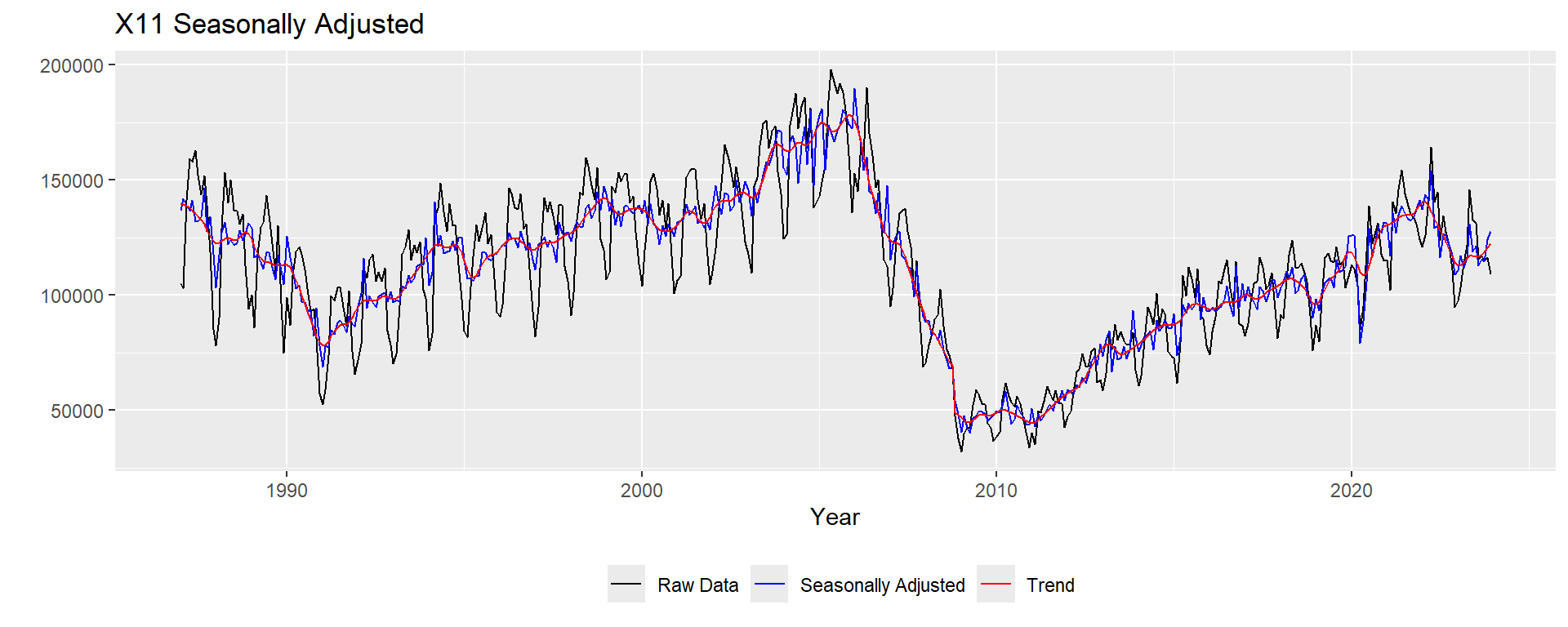
STL Decomposition
STL is an acronym for “Seasonal and Trend decomposition using Loess”, wherein Loess is a method for estimating nonlinear relationships.
stldecomp <- stl(df_ts[,"HousingStart"], s.window="periodic", robust=TRUE)
forecast::autoplot(stldecomp) +
ggtitle("STL Decomposition")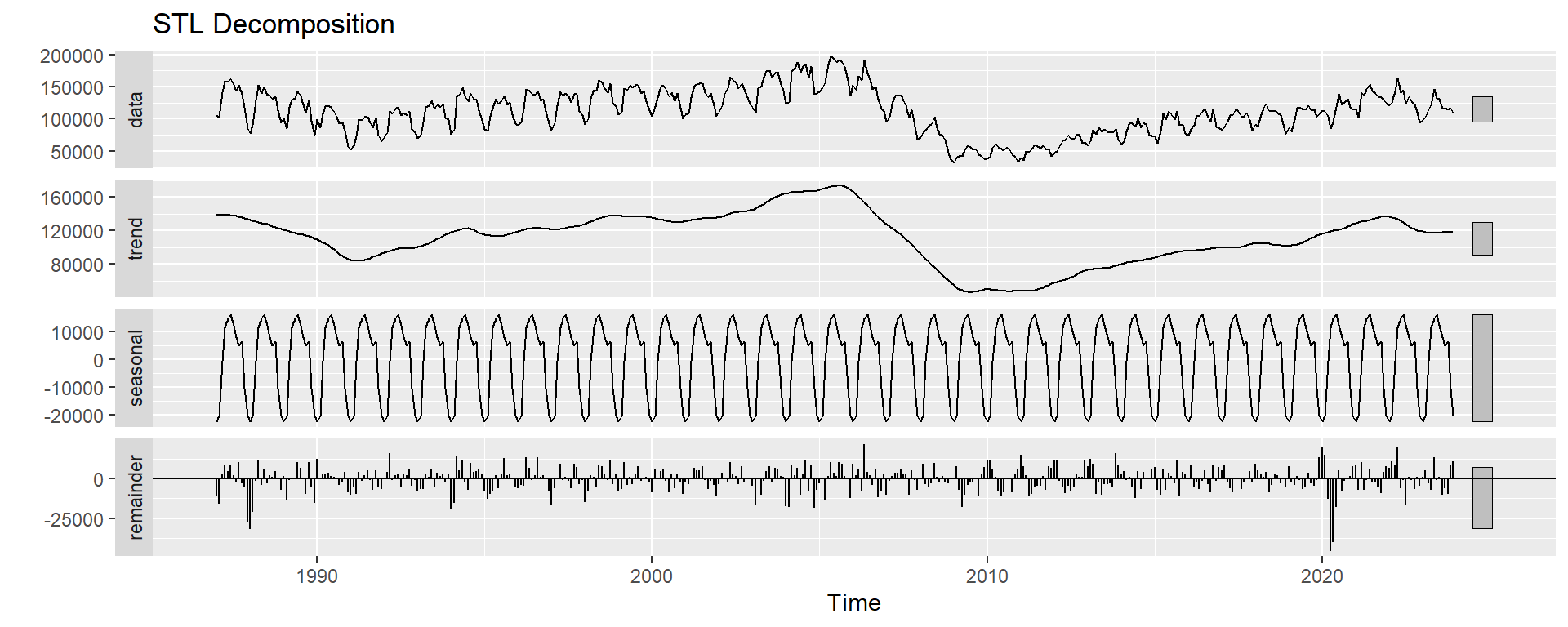
Loess is data intensive method and traditionally two-sided, meaning that we need data on either side of each point in order to apply the adjustment.
forecast::autoplot(df_ts[,"HousingStart"], series="Raw Data") +
autolayer(seasadj(stldecomp), series="Seasonally Adjusted") +
autolayer(trendcycle(stldecomp), series="Trend") +
xlab("Year") + ylab("") + labs(color = "") +
ggtitle("STL Seasonally Adjusted") +
scale_colour_manual(values=c("black","blue","red"), breaks=c("Raw Data","Seasonally Adjusted","Trend")) +
theme(legend.position="bottom")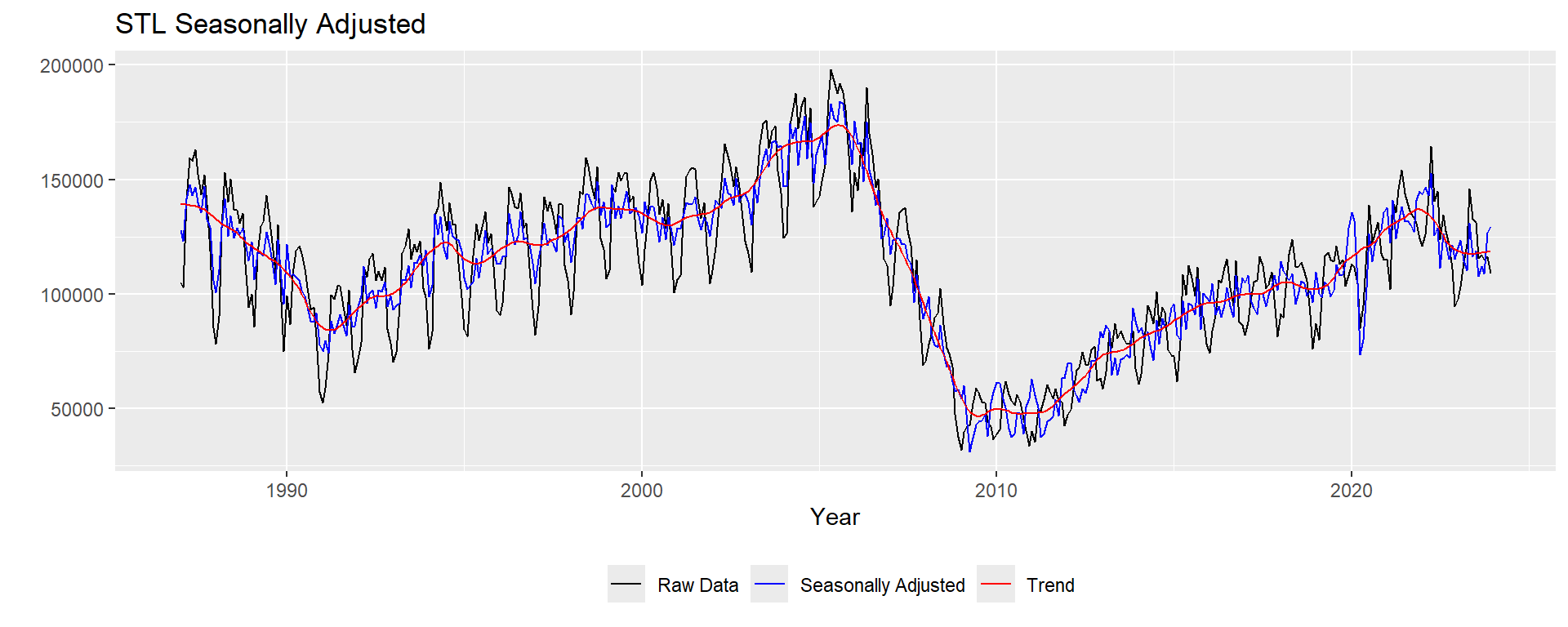
Compare the Decomp Methods
forecast::autoplot(df_ts[,"HousingStart"], series="Raw Data") +
autolayer(decomp$x-decomp$seasonal, series="Classical Additive Seasonally Adjusted") +
autolayer(seasadj(x11decomp), series="X11 Seasonally Adjusted") +
autolayer(seasadj(stldecomp), series="STL Seasonally Adjusted") +
xlab("Year") + ylab("") + labs(color = "") +
ggtitle("Seasonally Adjusted") +
scale_colour_manual(values=c("black","darkgreen","steelblue","darkred"),
breaks=c("Raw Data","Classical Additive Seasonally Adjusted",
"X11 Seasonally Adjusted", "STL Seasonally Adjusted")) +
theme(legend.position="bottom") + guides(colour = guide_legend(ncol = 2))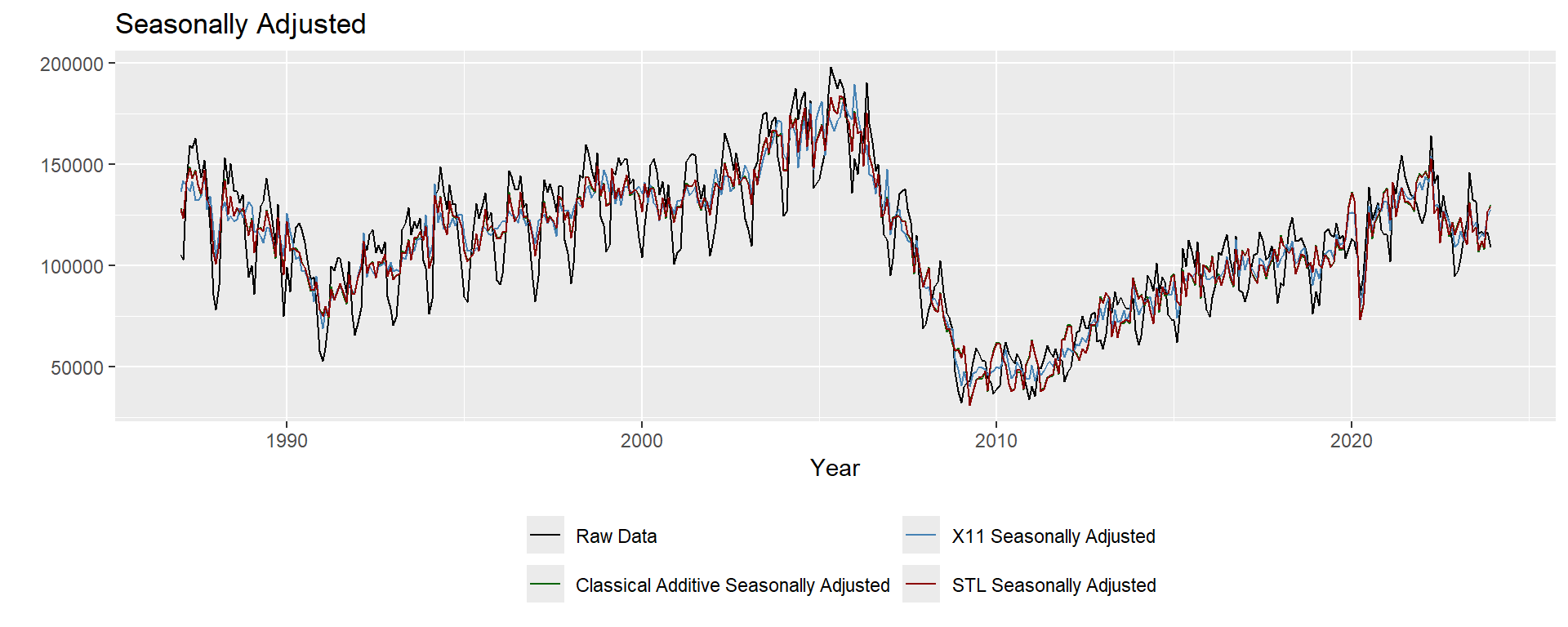
Note that this is NOT a forecasting exercise, so we don’t typically use some type of out of sample MSFE to determine which decomposition is best. We can investigate in sample behavior among the ``Noise” terms using MSE, AIC, and the like. Caution: x11 standardizes the noise and seasonal terms, so you can’t compare the 3 models directly, without some adjustments. (beyond our purview)
mean(decomp$random^2,na.rm = TRUE)[1] 61361365mean(resid(x11decomp)^2,na.rm = TRUE)[1] 0.005967311mean((stldecomp$time.series[3])^2,na.rm = TRUE)[1] 242347.5We could proceed exclusively with the seasonally adjusted series. But for instructional purposes, we’ll work with both the raw and seasonally adjusted series.
Stationarity
Stationarity is a time series concept regarding the behavior of the data in small windows of time.
Q: What does it mean that the ``first moment” is constant through time?
A: The average of the series is the same for the entire time horizon.
Q: What does it mean that the ``second moment” is constant through time?
A: The variance / volatility of the series doesn’t change over time.
Q: A stationary series is one in which the first and second moments are constant through time. (NOTE: There are actually many forms of stationarity. We’ll focus only on this characterization for now) Why is assuming stationarity helpful?
A:
- Consider a series that is not ``variance stationary”. It might have been relatively calm, with low variability. But then during COVID, volatility spikes. We should accommodate for this structural change within our model.
- Likewise, consider a series that is not ``mean stationary”. It might have a persistent upward trend. We should accommodate for this trend when attempting to find drivers of the series.
- Most standard time series modeling techniques require stationarity before implementing.
- Even those that don’t technically require stationarity could benefit from this type of behavior.
- Therefore, it’s essential we are able to detect and remedies any violations to this assumption.
Detect Non-Stationarity w/ADF
There are several tests to detect (non) stationarity.
The Augmented Dickey Fuller (ADF) test focuses on a manifestation of non stationarity called a unit root. A particular case of unit roots is the `Random Walk’ wherein today’s value is equal to yesterday’s + random noise.
Q: Why is the unit root popular in time series settings?
A: We often consider growth rates to be an object of interest. So, we are really interested in whether the difference in our time series is random; \(y_{t} = (1)y_{t-1}+e_{t}\) \(\Rightarrow\) \(y_{t}-y_{t-1}=e_{t}\), where \(e_{t}\) is random noise. If so, then we have a stationary process.
ADF Test
Ho: Non Stationary (Unit Root aka Random Walk)
Ha: Stationary
library(tseries)
adf.test(df_ts[,"HousingStart"])
Augmented Dickey-Fuller Test
data: df_ts[, "HousingStart"]
Dickey-Fuller = -2.3521, Lag order = 7, p-value = 0.4289
alternative hypothesis: stationaryadf.test(SA)
Augmented Dickey-Fuller Test
data: SA
Dickey-Fuller = -1.5802, Lag order = 7, p-value = 0.7552
alternative hypothesis: stationaryQ: Is our series stationary? Why do you suppose?
A:
- Notice the high pvalue implies we fail to reject (i.e. we have a non stationary series).
- This is true for both the raw series as well as the seasonally adjusted series.
- We saw previosly that these series have several changes in trend (dramatic drop and then a steady up turn).
Detect Non-Stationarity w/ KPSS
The Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test can be used in several ways. We’ll focus on its importance for testing trend stationarity (i.e. is the series stationary after adjusting for its trend).
H0: Trend Stationary
Ha: Not Trend Stationary
kpss.test(df_ts[,"HousingStart"], null="Trend")
KPSS Test for Trend Stationarity
data: df_ts[, "HousingStart"]
KPSS Trend = 0.50217, Truncation lag parameter = 5, p-value = 0.01kpss.test(SA, null="Trend")
KPSS Test for Trend Stationarity
data: SA
KPSS Trend = 0.54187, Truncation lag parameter = 5, p-value = 0.01Q: Is the series trend stationary? What is the implication?
A:
- Note the low pvalues imply that we reject and that we have both the raw and SA series that are not trend stationary.
- This implies that the seasonal osciallations were likely relatively steady over time, and thereby not engendering a non stationarity.
- If we can accommodate for the trend, we might be able to have a stationary process, which is ready for further modeling.
Detect Non-Stationarity w/ACF
Autocorrelation Function (ACF) tells us the correlation of a series with its own past.
The Partial Autocorrelation Function (PACF) tells us the autocorrelation of a series with its own past after correlation for the impact of other lags of the series.
The visualizations are collectively referred to as the (auto)correlogram.
library(astsa)
acf2(df_ts[,"HousingStart"], main = "ACF and PACF of Housing Starts Units")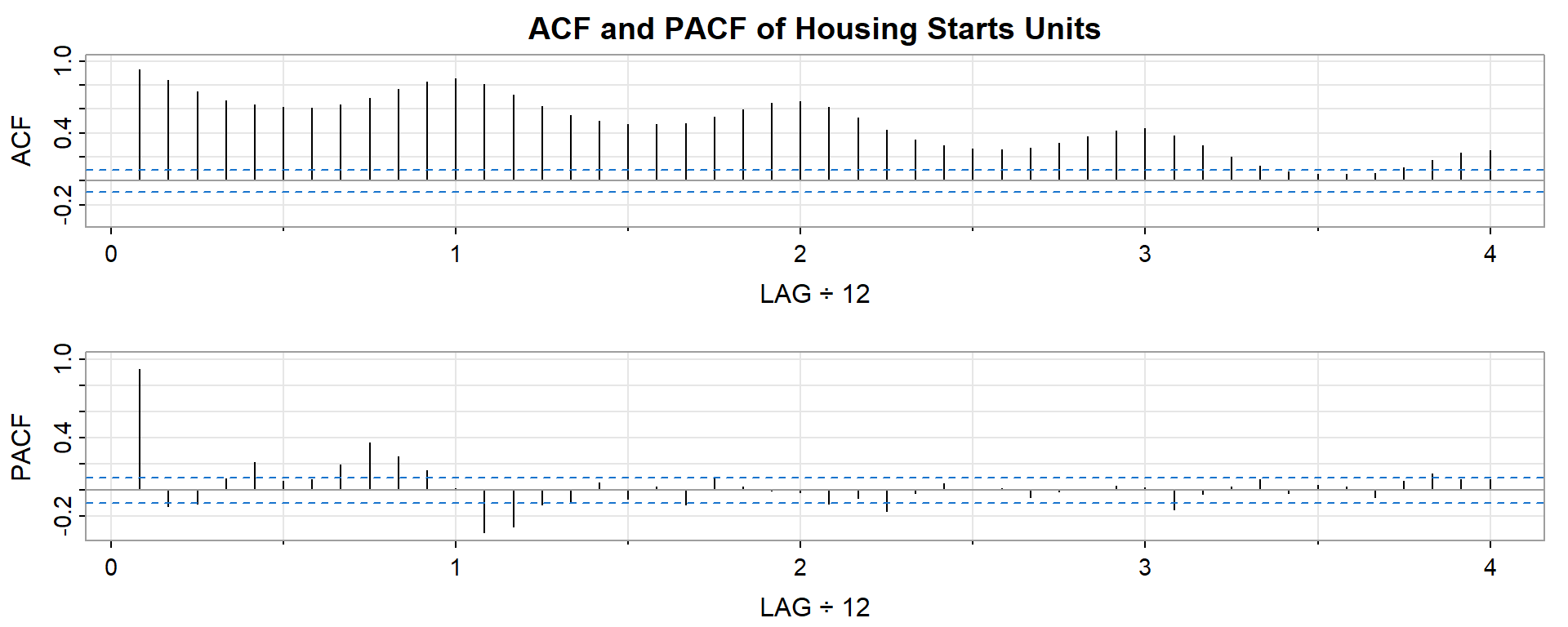
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
ACF 0.93 0.84 0.75 0.67 0.63 0.61 0.61 0.63 0.69 0.76 0.83 0.85 0.81
PACF 0.93 -0.12 -0.10 0.09 0.21 0.07 0.08 0.20 0.37 0.26 0.15 0.01 -0.32
[,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF 0.72 0.62 0.54 0.50 0.47 0.47 0.48 0.53 0.59 0.65 0.66 0.61
PACF -0.28 -0.11 -0.09 0.06 -0.07 0.02 -0.11 0.09 0.03 -0.01 -0.02 -0.11
[,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37]
ACF 0.53 0.42 0.34 0.30 0.27 0.26 0.27 0.31 0.37 0.42 0.43 0.38
PACF -0.06 -0.16 -0.03 0.05 0.01 0.01 -0.05 -0.01 0.01 0.03 0.02 -0.15
[,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
ACF 0.29 0.20 0.13 0.08 0.06 0.05 0.06 0.11 0.17 0.23 0.25
PACF -0.03 0.02 0.08 -0.02 0.04 0.03 -0.06 0.07 0.13 0.08 0.08Q: What does the first bar in the ACF mean? What does the second bar in the ACF mean?
A:
- First Bar: The correlation between housing starts in month t has a roughly .9 correlation with housing starts in month t-1.
- Second Bar: The correlation between housing start in month t has a roughly .8 correlation wth housing starts in month t-2.
Q: What does the first bar in the PACF mean? What does the second bar mean?
A:
- First Bar: The correlation between housing starts in month t has a roughly .9 correlation with housing starts in month t-1. (i.e. it’s the same as the ACF)
- Second Bar: After controlling for the effects of month t-1, housing starts in month t have a slight negative correlation with housing starts in month t-2.
Q: How do we use the Correlogram to understand the presence of seasonality?
A:
- The ACF depicts a seasonal pattern (notice the wave cresting every 12mhts).
- The PACF exhibits strong persistence near the 1st lags, which might be helpful when we model the process with its own past lags (e.g. ARMA).
Remedy w/Differencing
A common approach to overcoming non stationarity is by taking the (percent) difference in the series. Often, if a series is non-stationary, then computing the \(\Delta x_{t}=x_{t}-x_{t-1}\) is stationary. If the first difference is not stationary, we can compute a second difference analogously.
Often in our modeling process these growth rates are the objects of interest, which aids our interpretation of any results.
Let’s first difference the Housing Starts series and recompute the ADF test.
FirstDiff <- diff(df_ts[,"HousingStart"]) # compute the first difference in housing
FirstDiff <- na.omit(FirstDiff) #clean up the data
plot(FirstDiff) 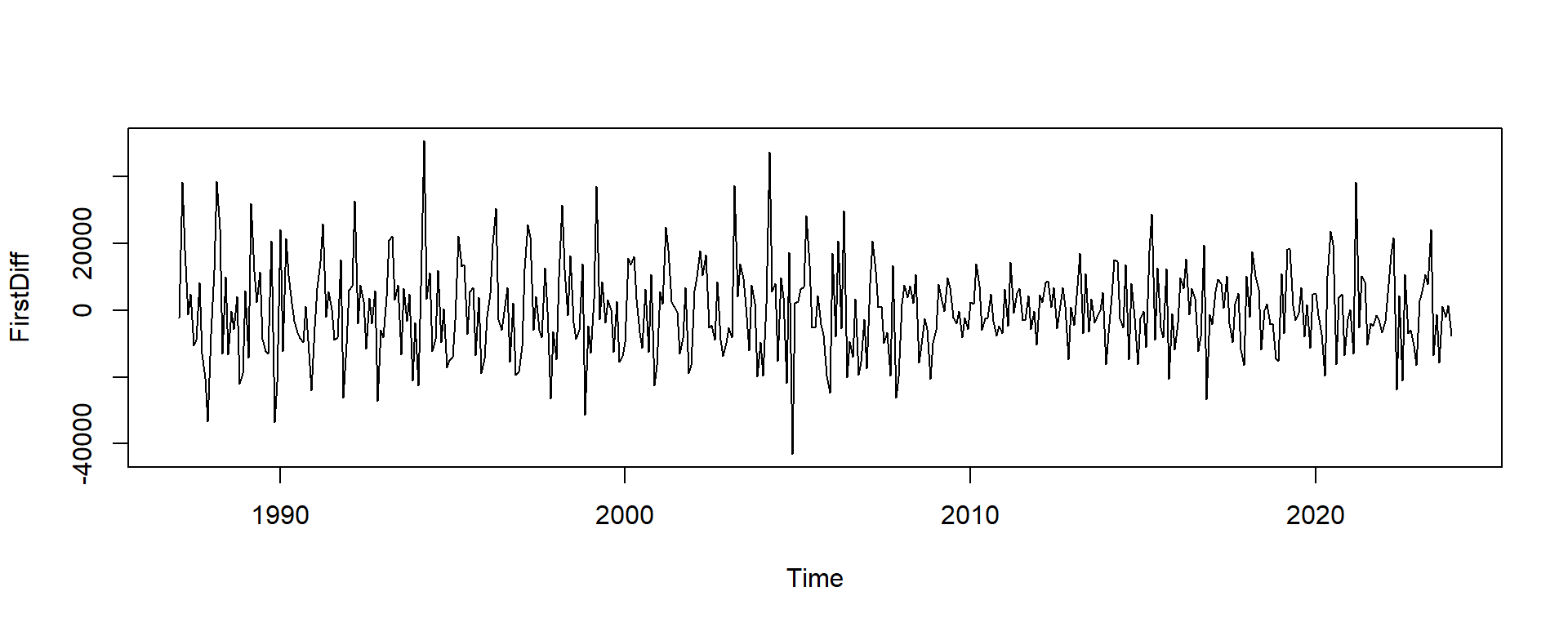
adf.test(FirstDiff)
Augmented Dickey-Fuller Test
data: FirstDiff
Dickey-Fuller = -16.453, Lag order = 7, p-value = 0.01
alternative hypothesis: stationaryQ: Does you ``see” a stationary process? Does the suggest stationarity?
A:
- Notice that the low pvalue suggests we now have a stationary process.
- This is confirmed by visual inspection of the time series plot, which has roughly similar mean and variance throughout the time series.
We can also accommodate for seasonality within our differencing method by taking year-over-year growth rates.
SeasDiffFirstDiff <- diff(FirstDiff,lag = 12)
plot(SeasDiffFirstDiff)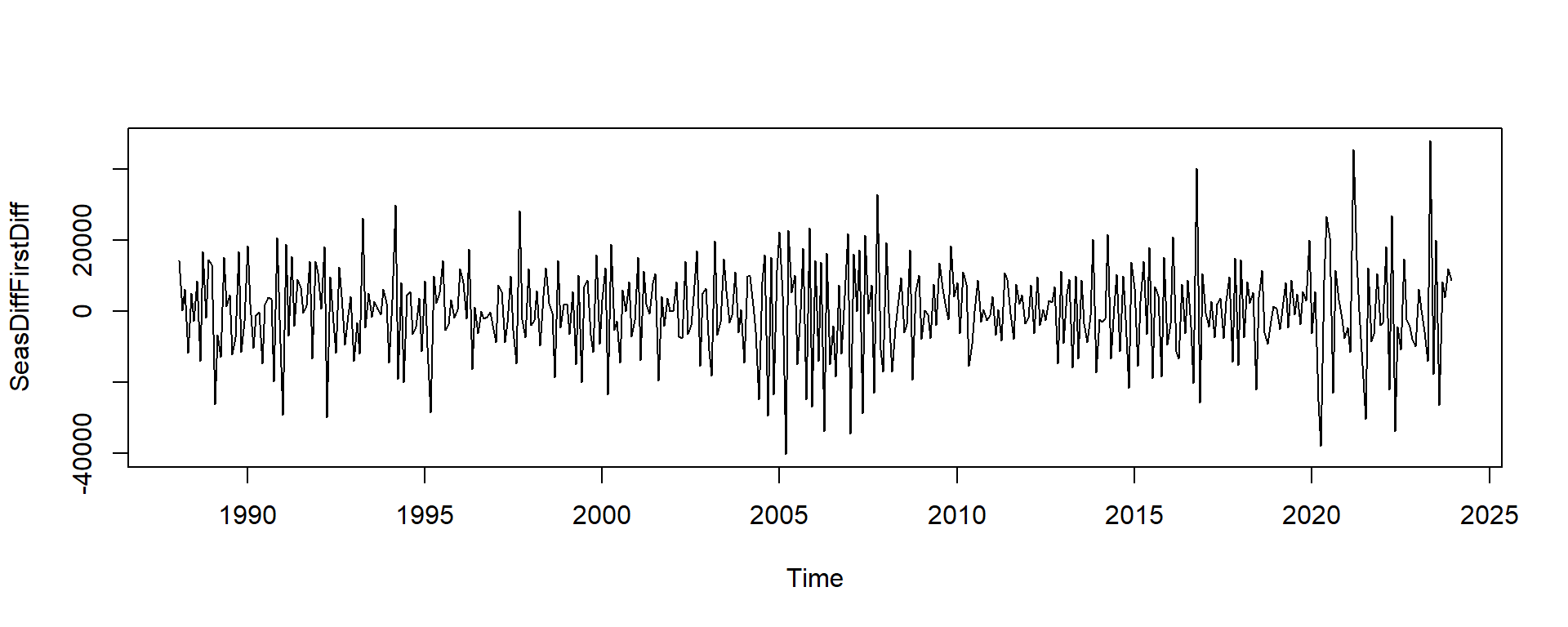
adf.test(SeasDiffFirstDiff)
Augmented Dickey-Fuller Test
data: SeasDiffFirstDiff
Dickey-Fuller = -8.7369, Lag order = 7, p-value = 0.01
alternative hypothesis: stationaryPro Tip: Converting your series to logs and then computing the difference approximates a growth RATE.
Converting to growth rates is also helpful to standardize our features. So, let’s do that for housing starts.
library("quantmod")
HousingStartGrowth = na.omit(Delt(df_ts[,"HousingStart"]))*100 # convert to growth rateQ: Is the growth rate stationary?
adf.test(HousingStartGrowth)
Augmented Dickey-Fuller Test
data: HousingStartGrowth
Dickey-Fuller = -15.47, Lag order = 7, p-value = 0.01
alternative hypothesis: stationaryA: Notice again that the low pvalue indicates stationarity.
Housing Prices: Stationarity
Q: Are prices stationary?
adf.test(df_ts[,"PriceIndex"])
Augmented Dickey-Fuller Test
data: df_ts[, "PriceIndex"]
Dickey-Fuller = -1.069, Lag order = 7, p-value = 0.9272
alternative hypothesis: stationaryplot(df_ts[,"PriceIndex"])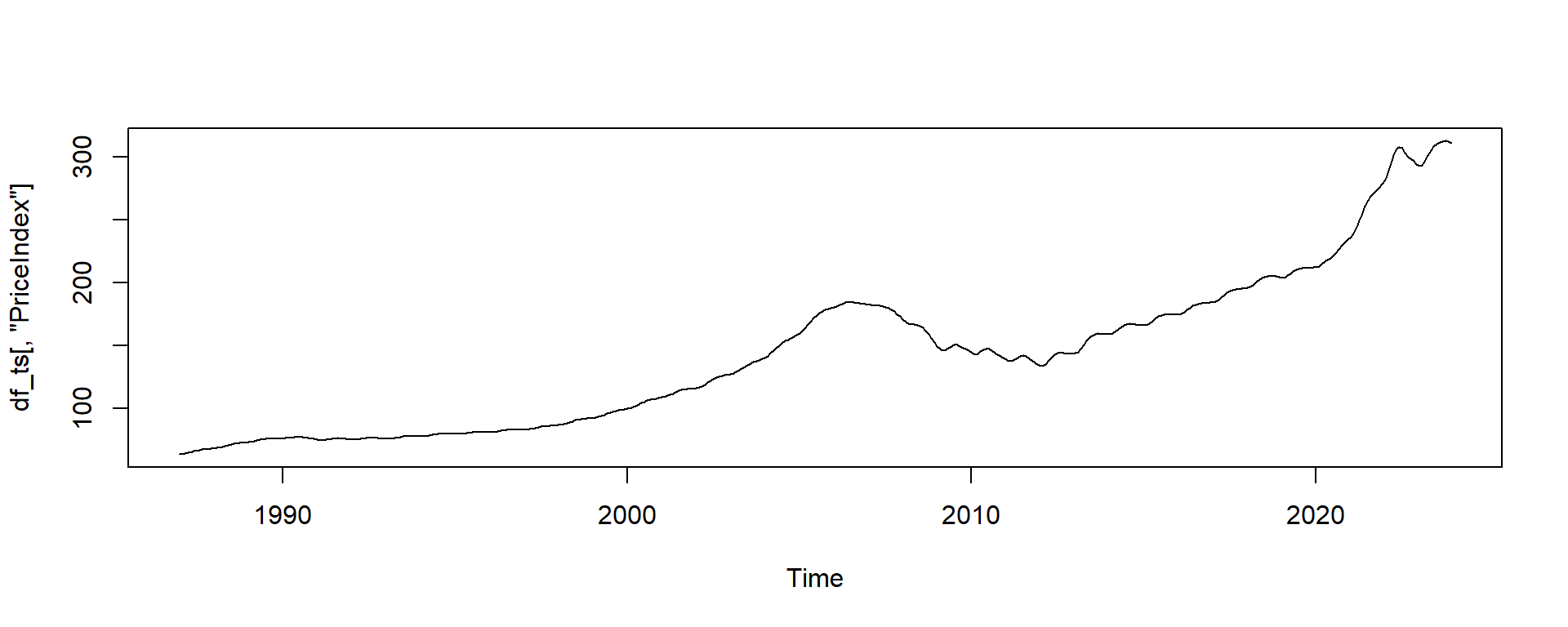
A:
- The high pvalue suggests non-stationarity.
- There is a clear trend and a structural change around the 2008 crash.
Let’s compute a 1st difference
PriceIndexGrowth = na.omit(Delt(df_ts[,"PriceIndex"]))*100
adf.test(PriceIndexGrowth)
Augmented Dickey-Fuller Test
data: PriceIndexGrowth
Dickey-Fuller = -3.4477, Lag order = 7, p-value = 0.04756
alternative hypothesis: stationaryplot(PriceIndexGrowth) 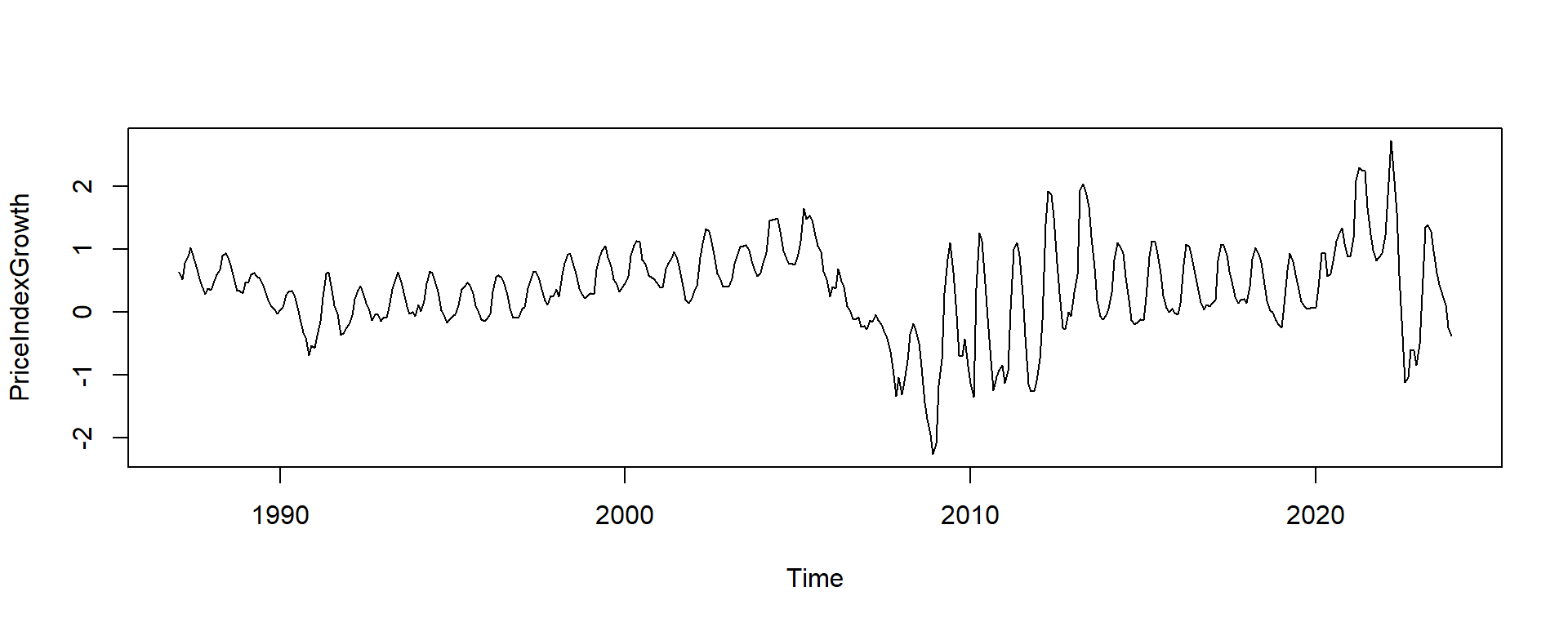
Q: Is the growth rate in prices stationary?
A: Notice the mildly high pvalue suggesting possible non stationarity. That could be due to the oscillation from seasonal patterns and the structural changes around the 2008 crash.
So let’s adjust that Growth series for seasonality.
#PriceIndexGrowth_decomp<-decompose(df_ts[,"PriceIndex"], type="additive")
PriceIndexGrowth_decomp<-decompose(PriceIndexGrowth, type="additive")
PriceIndexGrowthSA = PriceIndexGrowth - PriceIndexGrowth_decomp$seasonal
plot(PriceIndexGrowthSA)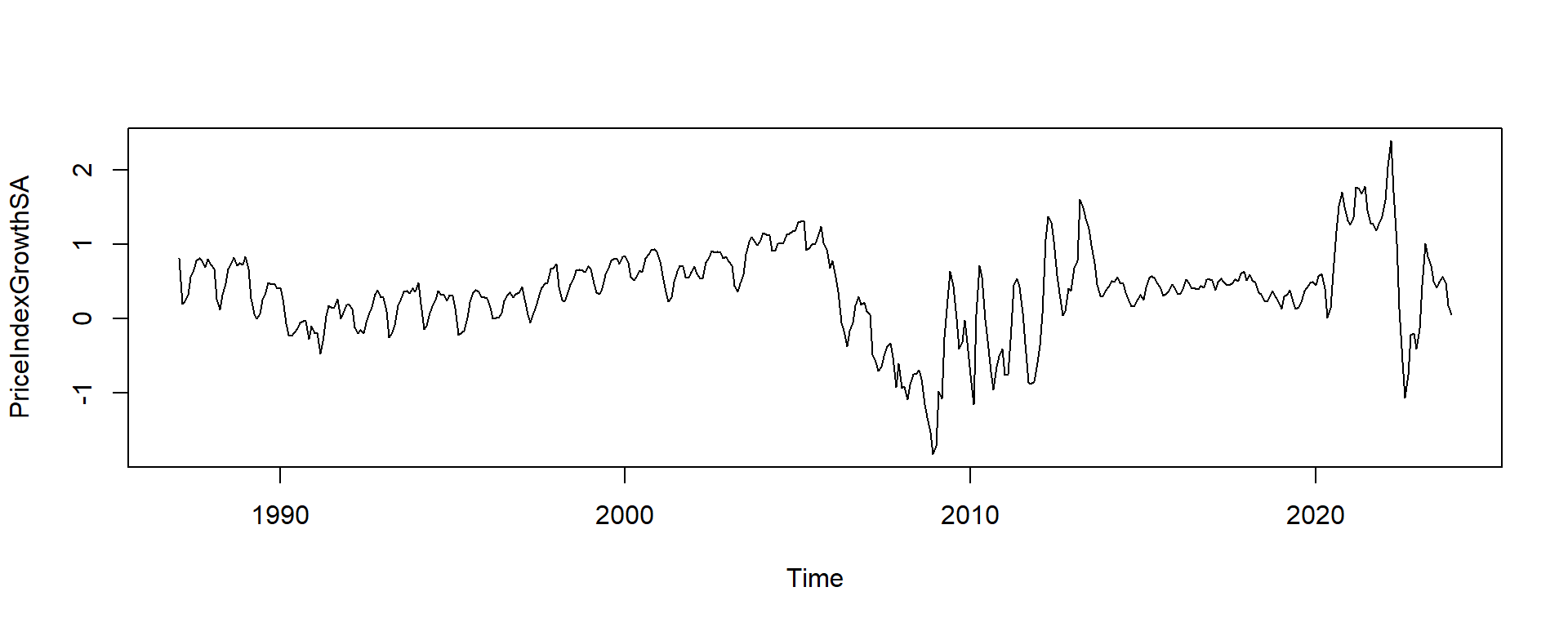
adf.test(PriceIndexGrowthSA)
Augmented Dickey-Fuller Test
data: PriceIndexGrowthSA
Dickey-Fuller = -3.1864, Lag order = 7, p-value = 0.09035
alternative hypothesis: stationaryQ: Is this seasonally adjusted growth series stationary? What’s the implication?
A:
- The low pvalue now suggests a stationary series.
- There are several structural features in the price series (the crash, the trend, the varying seasonality) that need to be addressed before we can model this series.
Prep the df
Let’s group all of these adjusted series together
df_adj <- data.frame(cbind(HousingStartGrowth, PriceIndexGrowthSA)) %>%
`colnames<-`(c("HousingStartGrowth","PriceIndexGrowthSA"))
df_adj$Date <- df$Date[c(-1)]
#df_adj<-na.omit(df_adj)Time Series EDA
Now that we have adjusted our data series, let’s examine their time series properties.
AutoCorrelogram
tsdisplay(df_adj$HousingStartGrowth, main = "Time Series Plot of Housing Start Units Growth")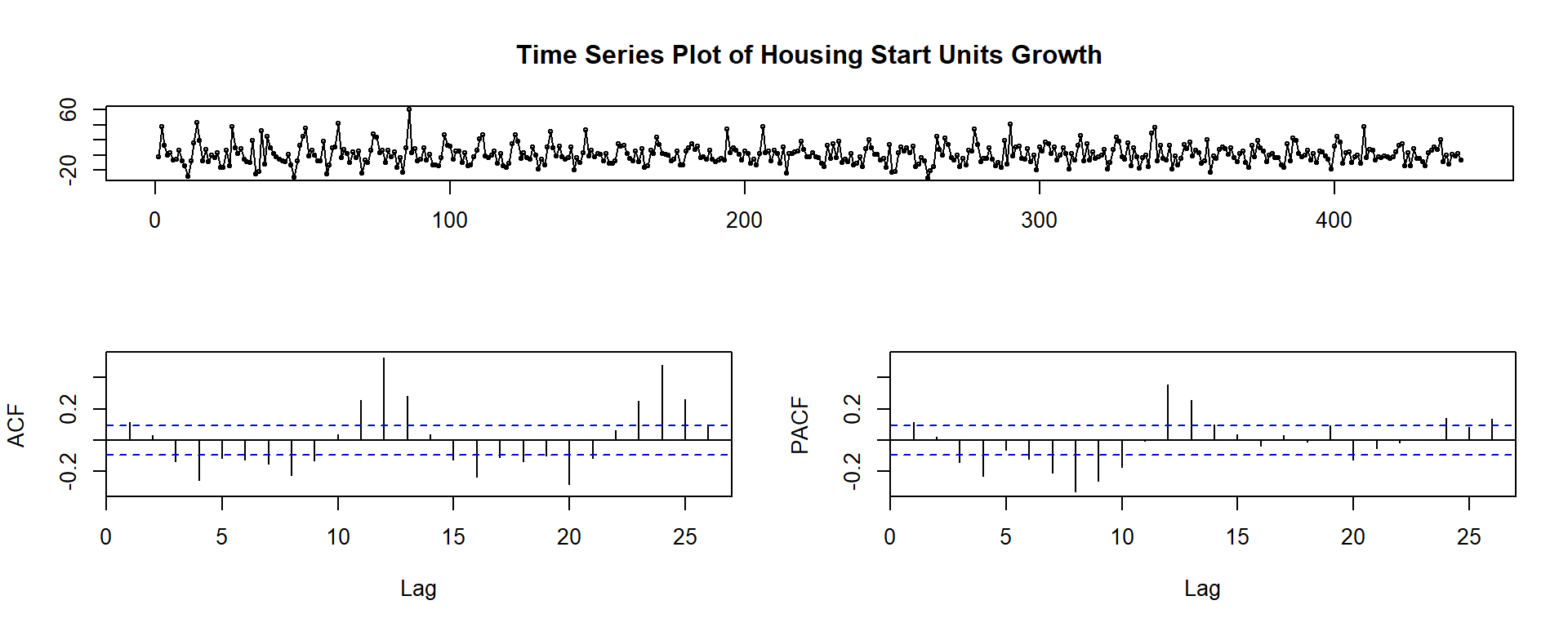
Q: What do the ACF and PACF suggest?
A: The spikes in the auto correlogram beyond the blue bars suggest a significant some significant short term persistence that we can incorporate into our modeling strategy later.
Let’s inspect the price series.
tsdisplay(df_adj$PriceIndexGrowthSA, main = "Time Series Plot of SA Price Index Growth")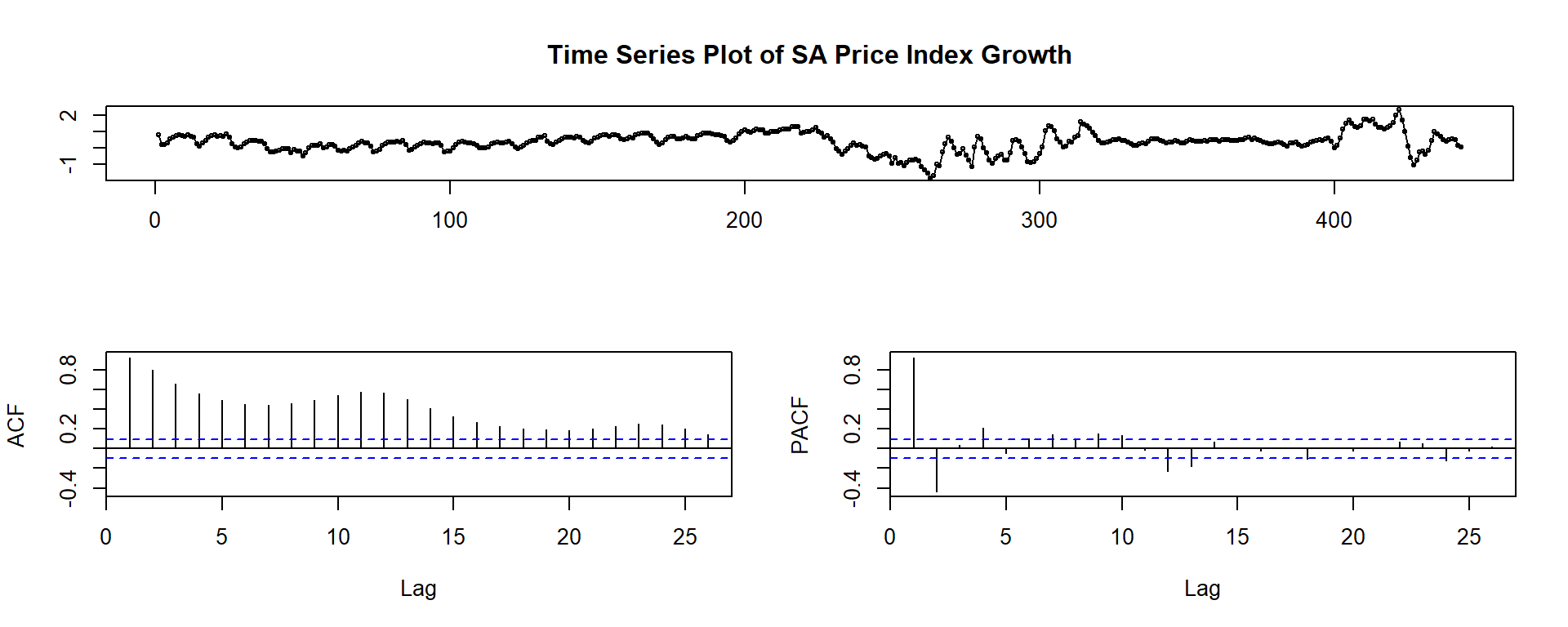
Q: What does the autocorrelogram suggest about the series?
A:
- The oscillation in the ACF suggests a bit of seasonality remains.
- The decline in the ACF and the two spikes in the PACF suggest short term persistence in the series. We can leverage this when we model the series.
Cross Correlations
Sometimes series lead/lag one another for `economic’ reasons. We can visualize and detect this cross auto correlations with a CCF (Cross Correlation Function).
Q: Why might prices LEAD starts?
A: Higher prices implies higher incentives to build homes. The home building process takes many months, hence the lead time from price signal to housing start action.
Q: Why might prices LAG starts?
A: Higher starts increase the supply on the market, relative to demand, which may impact prices. This make take time since the housing market clears slows (i.e. it takes time for someone to decide to sell, then put their home on the market, etc..)
Here we’ll examine whether growth of housing starts lead or lag price growth.
ccfvalues = ccf(x=df_adj$HousingStartGrowth, y=df_adj$PriceIndexGrowthSA,
main = "CCF of Housing Start Growth and Price Index Growth", lag.max = 24)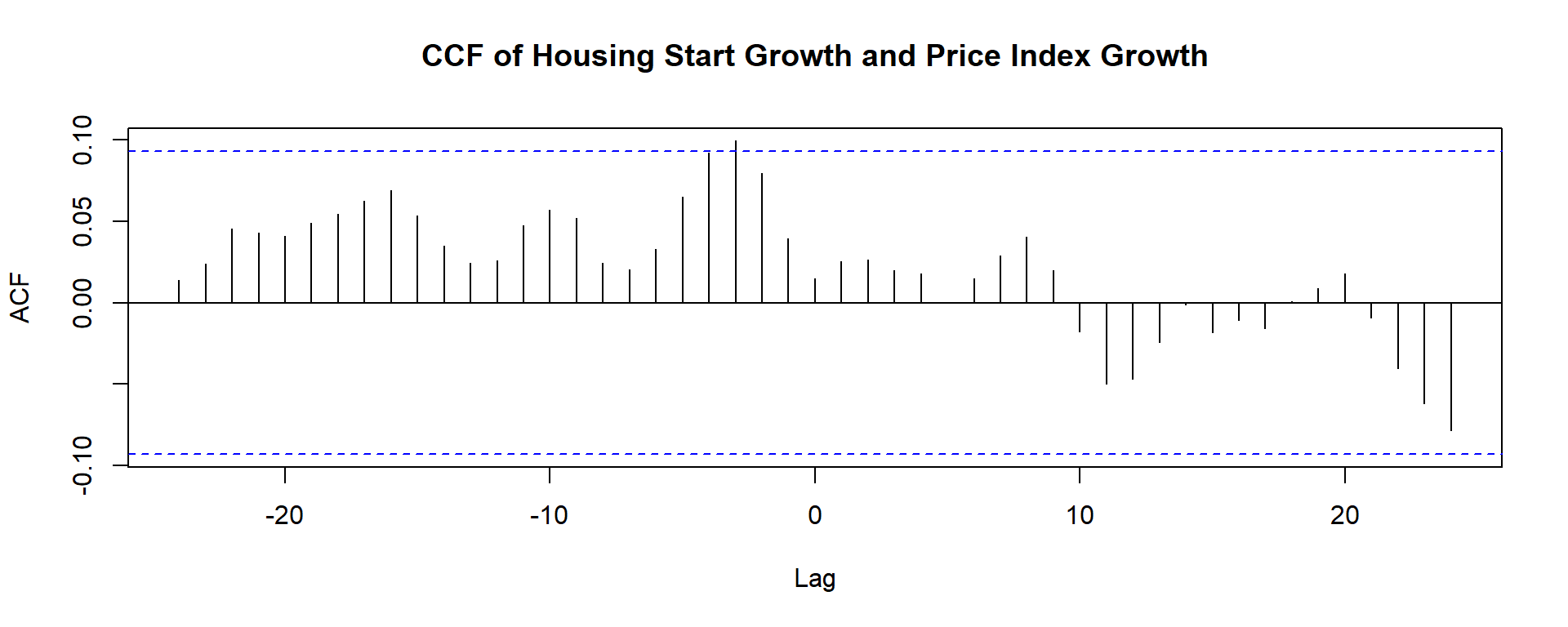
When lag = -1 we are computing the cor(HousingStart_t-1, Price_t); i.e. Starts LEAD Prices.
When lag = +1 we are computing the cor(HousingStart_t+1,Price_t); i.e. Starts LAG Prices.
Positive values indicate that the series move together. Negative values indicate the series move in opposite directions.
The blue lines provide a 95% CI.
Q: What is the implication of the graphic?
A:
- The spikes are more prominent in the negative lag area, suggesting possible leading effects for housing starts.
- A model such as \(Prices_{t} = \alpha + \beta HousingStarts{t-1} + e_{t}\) might be useful for explaining/forecast prices.
- However, there is not as much information in prices to forecast future housing starts.
- Regardless of the direction, neither series has statistically significant lead/lag effects, and thus may not be helpful for modeling.
Here is an alternative visualization.
library(astsa)
HSGrowth <- df_adj$HousingStartGrowth
PriceGrowth <- df_adj$PriceIndexGrowthSA
lag2.plot(series1 = HSGrowth,
series2 = PriceGrowth,
max.lag = 11) 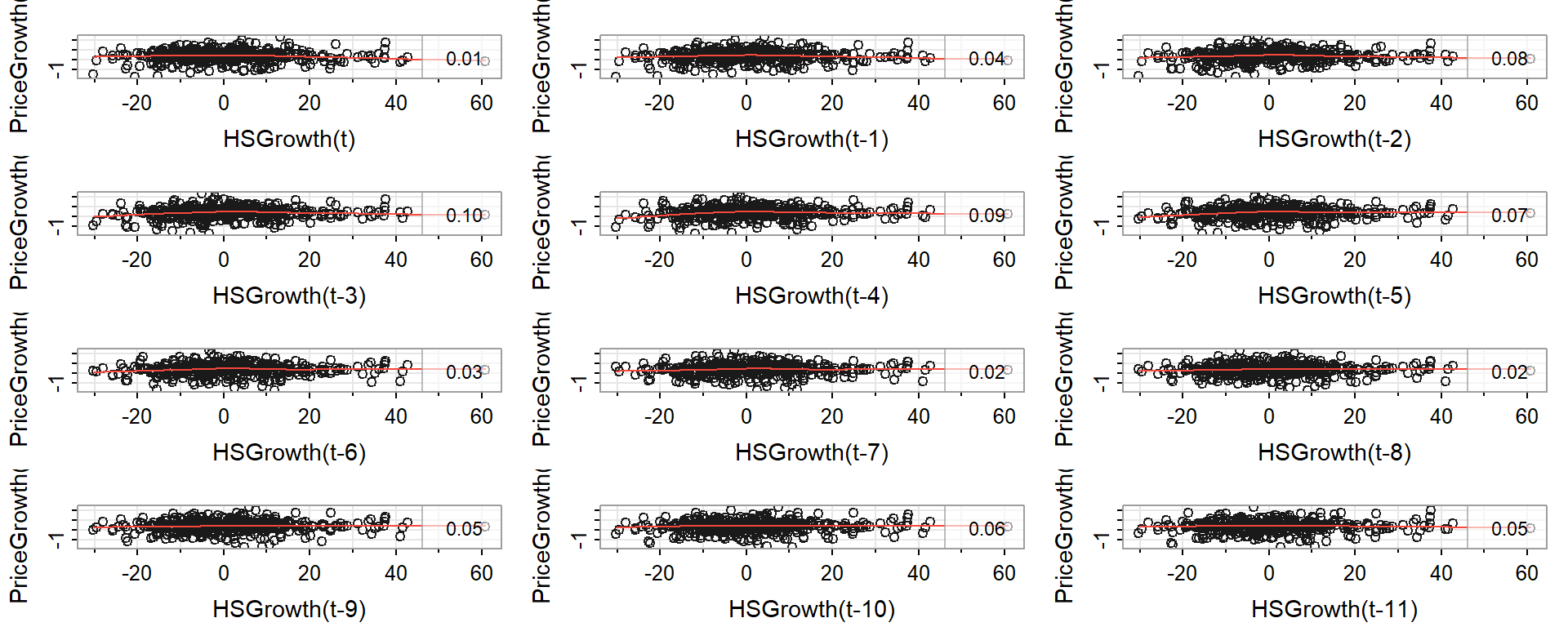
# Note: series1 is the one that gets lagged. Q: What are the lagged scatter plots suggesting?
A: There is not much power in lagged prices for explaining housing starts growth.
Explain
Now that we’ve explored our data’s temporal patterns let’s attempt to explain its movements. We’ll do so with traditional and time series econometric techniques.
Regression
Since we are dealing with time series data we need to be careful about what information we are using and WHEN that occurs. Let’s focus on a CONTEMPORANEOUS regression, wherein we are using data at time t to explain our outcome variable (housing prices) at time t.
\[ Price_{t}=\alpha + \beta Starts_{t} + u_{t}\] Q: What do we assume about the errors of this model?
A:
- Among other things, we assume that the errors are independent of each other.
- In our time series setting, that means the errors in January are not related to the errors in February, etc..
- This is a sickness called serial correlation, wherein the errors exhibit autocorrelation.
- If your model is plagued by serial correlation your estimators typically remain unbiased, but are not efficient.
LinearModel = lm(PriceIndexGrowthSA ~ HousingStartGrowth, data = df_adj)
summary(LinearModel)
Call:
lm(formula = PriceIndexGrowthSA ~ HousingStartGrowth, data = df_adj)
Residuals:
Min 1Q Median 3Q Max
-2.17309 -0.26871 0.03384 0.32403 2.02001
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.359469 0.027742 12.96 <2e-16 ***
HousingStartGrowth 0.000657 0.002121 0.31 0.757
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5828 on 441 degrees of freedom
Multiple R-squared: 0.0002175, Adjusted R-squared: -0.00205
F-statistic: 0.09596 on 1 and 441 DF, p-value: 0.7569Q: Interpret the coefficient on HousingStartGrowth? Focus on its significance.
A:
- The impact is not statistically significant.
- i.e. the growth rate of housing starts in this month does not help to explain the seasonally adjusted growth rate of prices in this month.
- If our model is ``sick” with serial correlation, this t-stat could be contaminated, and give us misleading conclusions.
Detect Serial Correlation
There are myriad visual and formal tests for serial correlation. Most operate on the residuals of the model.
Visual inspection
Let’s inspect our residuals for troublesome patterns.
checkresiduals(LinearModel)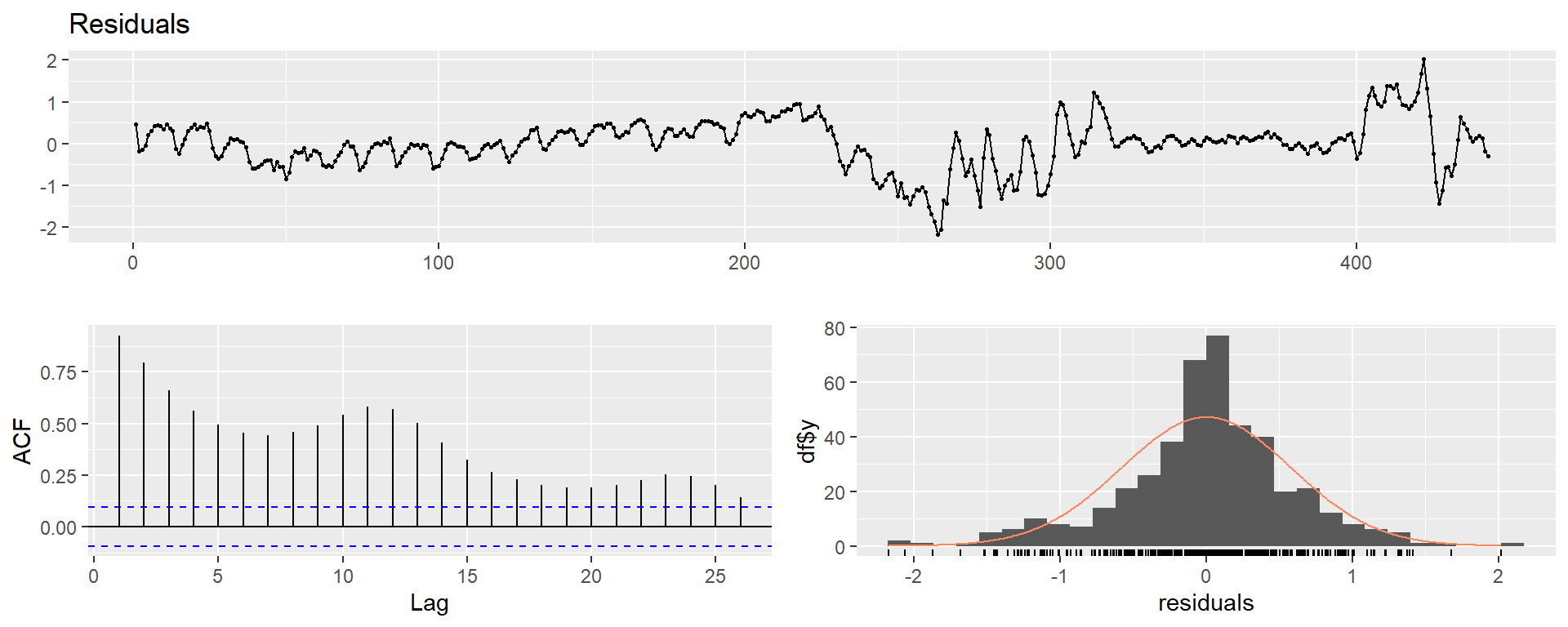
Breusch-Godfrey test for serial correlation of order up to 10
data: Residuals
LM test = 398.14, df = 10, p-value < 2.2e-16Q: What does this visualization tell you about the presence of serial correlation and the model in general?
A:
- Notice the spikes in the residual ACF.
- These are indicative of some type of omitted temporal pattern, which might suggest the presence of serial correlation.
- Also notice that the model does not seem to work well around the 2008 crash and COVID. These structural changes could impede our ability to detect the underlying relation between starts and prices.
Durbin Watson Test
The Durbin Watson (DW) test asks whether the model residuals are auto correlated.
Ho: No auto correlation in residuals
Ha: Auto correlation in residuals
library(lmtest)
dwtest(formula = LinearModel, alternative = "two.sided")
Durbin-Watson test
data: LinearModel
DW = 0.14591, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is not 0Q: Interpret the test.
A: The small pvalue suggests there is autocorrelation.
BG Test
Breusch Godfrey (BG) Test
Ho: Model residuals not autocorrelated
Ha: Model residuals are autocorrelated
bgtest(formula = LinearModel)
Breusch-Godfrey test for serial correlation of order up to 1
data: LinearModel
LM test = 380.34, df = 1, p-value < 2.2e-16Q: Interpret the test.
A: The small pvalue suggests there is autocorrelation.
LB Test
Ljung Box Test
Ho: Model residuals not autocorrelated
Ha: Model residuals are autocorrelated
Box.test(residuals(LinearModel), type = "Ljung-Box")
Box-Ljung test
data: residuals(LinearModel)
X-squared = 382.48, df = 1, p-value < 2.2e-16Q: Interpret the test.
A: The small pvalue suggests there is autocorrelation.
Remediating Serial Correlation
If we are lucky enough to know the precise form of the serial correlation, then we can include it directly in our modeling via GLS. However, that is seldom the case in practice. So, we rely upon HAC (heteroscedasticity and autocorrelation consistent) standard errors.
library(sandwich)
NW_VCOV_LinearModel <- NeweyWest(LinearModel, prewhite = F, adjust = T) # The pre-whitening and adjust are set to F, and T respectively to ensure the proper formula and small sample adjustments are made.
# Compute Standard Errors
HAC_err=sqrt(diag(NW_VCOV_LinearModel))
HAC_err (Intercept) HousingStartGrowth
0.057186640 0.002617528 Let’s see if this new std error is meaningful.
Q: As a reminder, how do we compute the t stat by hand from the Linear Model?
A:
summary(LinearModel)$coefficients Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.3594694216 0.027742107 12.9575385 9.190799e-33
HousingStartGrowth 0.0006570052 0.002120934 0.3097716 7.568809e-01LinearTValue = summary(LinearModel)$coefficients[2,1]/summary(LinearModel)$coefficients[2,2]
LinearTValue[1] 0.3097716Q: How do we recompute with the new HAC std error? What’s the implication for our model?
HACTValue = summary(LinearModel)$coefficients[2,1]/HAC_err[2]
HACTValueHousingStartGrowth
0.2510022 A:
- Notice the (slight) differences in the standard errors.
- The t value has not changed much.
- The implication is that eventhough there was a statistical presence of serial correlation, this remedy did not change the outcome (i.e. housing start growth is not a significant driver of future price growth)
- That could mean that HAC hasn’t adequately dealt with the serial correlation, or that the problem was not pervasive.
- We can iterate our test and remediation process, but will forgo that for the sake of this exercise.
Rolling Regression
Consider running a regression from Jan87 through Dec97 and grabbing \(\beta\).
Then run the regression again on Feb87 through Jan98, and grabbing the \(\beta\).
Q: What’s the potential value in this approach?
A:
- An important feature of time series models is coefficient stability. i.e. is the `economic’ process stable through time?
- We can investigate by running our model over small windows through time.
- If the coefficients change often/suddenly, it implies something is misspecified in our model.
Moving Window
Let’s run our regression over a fixed window of 30 periods, grab the results, then move the 30 period window forward by one month, rerun the regression, and repeat until the end of the sample.
library(tidyfit)
library(tidyr)
library(purrr)
library(lubridate)
library(stringr)
library(ggplot2)
RollingReg<-df_adj %>%
regress(PriceIndexGrowthSA~HousingStartGrowth,
m("lm",vcov.="HAC"),
.cv = "sliding_index", .cv_args=list(lookback=months(30),index = "Date"),
.force_cv= TRUE, .return_slices=TRUE)
beta.df<-coef(RollingReg)
beta.df <- beta.df %>%
unnest(model_info) %>%
filter(term=="HousingStartGrowth") %>%
mutate(upper = estimate + 2 * std.error, lower = estimate - 2 * std.error) %>%
mutate(beta = estimate)
beta.df %>%
mutate(Dates = as.Date(slice_id)) %>%
filter(term == "HousingStartGrowth") %>%
ggplot(aes(Dates)) +
geom_ribbon(aes(ymax = upper, ymin = lower), alpha = 0.25) +
geom_line(aes(y = beta)) +
theme_bw(8)
Q: What is the rolling window graph suggesting about our model?
A:
- beta is the explanatory power of housing start growth in month t upon SA price growth in month t.
- There seems to be structure changes during the housing crash of 2008 and the COVID spike. - We might want to include dummies / control variables to accommodate for these periods.
- 30 periods is rather arbitrary. We should tune that parameter, but we won’t for the sake of time.
Forecast
Now that we’ve explored the data and have explained its movements, we can attempt to forecast. There are myriad models to forecast a time series. Some use exogenous features (e.g. housing starts lags to forecast housing prices), while others use the series’ own temporal persistence (i.e. today is a good predictor for tomorrow). We will explore a few common approaches.
Training and Test Samples
Q: Why can’t we do a conventional test/train split on time series data? i.e. take a random subsample of (let’s say) 80% of the data to train, and the remaining 20% to test?
A:
- The temporal persistence of the data means that each observation is connected to the others. Randomly breaking them apart loses valuable information
- There is danger of leakage. We can’t train on 2023 and test on 2022. The DGP of 2023 is built from the behavior of 2022. This is cheating.
- There is danger of leakage. We can’t train on 2023 and test on 2022. The DGP of 2023 is built from the behavior of 2022. This is cheating.
- Relatedly, typical cross validation techniques are in danger of similar issues with time series.
Q: So, how should we structure train/test samples for time series?
A:
- We typically order the observations by time (they already are) and chose the most recent “x” observations as testing and all dates prior to train.
- The size of the test/train split remains an choice that we should stress test, just as we do with cross sectional models.
- Moreover, we need to ensure that our training sample has similar structural characteristics as our test sample. e.g. we want to avoid training housing prices 2010-2019 and then test in 2020 amid the COVID shock.
For our example we will use
Train: Jan1987-Dec2013
Test: Jan2014-end of sample
We could create separate dataframes from each subsample, but we will avoid that in order to illustrate some subseting features of the functions we will use.
Let’s adjust the dataframe into a time series object so that we can take advantage of certain time series features.
df_adjts <- ts(df_adj, start = c(1987,02), frequency = 12)Distributed Lag
A distributed lag model forecasts a series with past values of some exogenous series (depicted here with one lag). \(Price_{t}=\alpha + \beta Starts_{t-1} + u_{t}\).
An autoregressive distributed lag (ADL) also includes lagged values of Price (depicted here with one lag). \(Price_{t}=\alpha + \beta Starts_{t-1} + \gamma Price_{t-1} + u_{t}\).
Q: What does \(\gamma\) mean?
A: The impact of a price change this month on price changes next month.
We can use the CCF to detect leads/lags in our training sample.
ccf(x=window(df_adjts[,"HousingStartGrowth"], end = c(2013,12)),
y=window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)),
main = "CCF of Housing Start Growth and Price Index Growth") 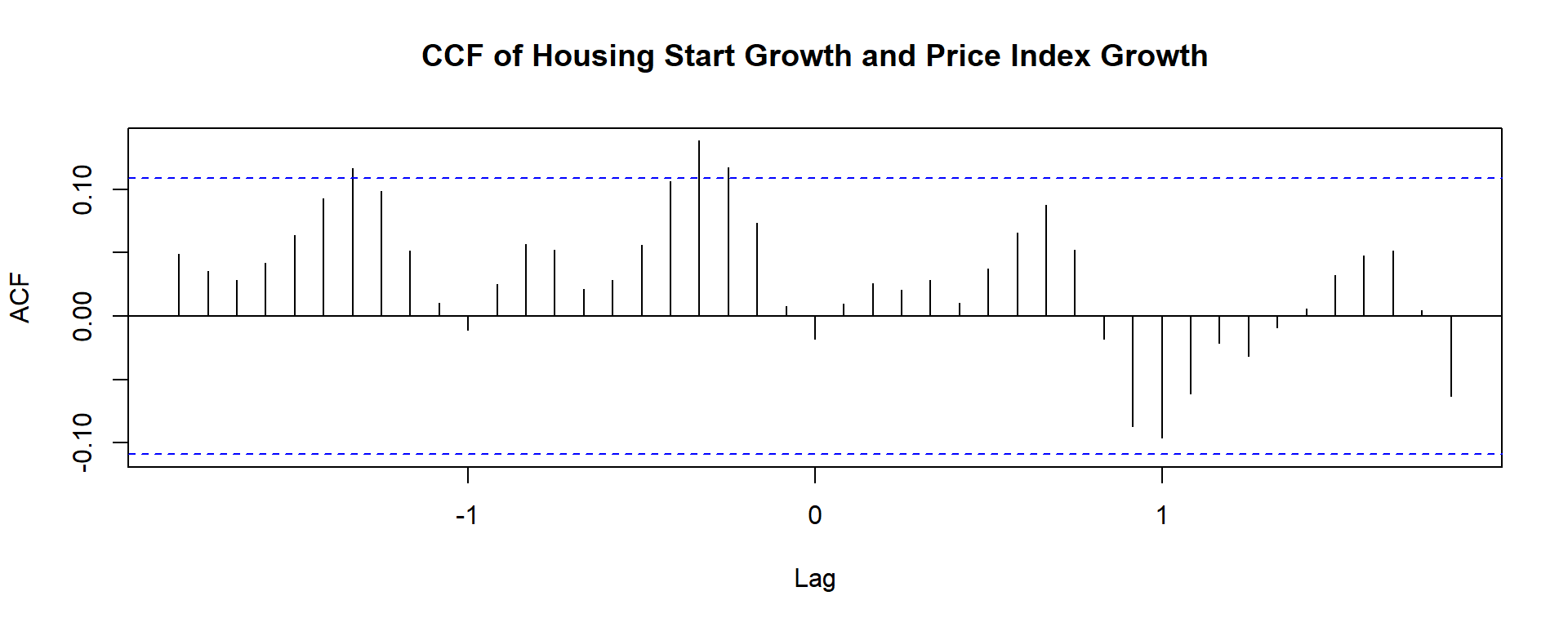
Q: What does the CCF suggest about the structure of a forecasting model?
A:
- The spikes within the negative lag regions suggests that Starts appear to have some predictive power over future prices.
- However, these spikes aren’t strongly significant, so we proceed with caution.
- The reverse doesn’t seems to be true (But, we’ll explore such situations with tools later)
- Given the temporal persistence of the price series, let’s try an ADL model. We’ll demonstrate with 2 lags on price growth and 12 on starts. We can also use information criterion to guide lag selection.
ADL_alldata <- ts.intersect(df_adjts,
PriceIndexGrowthLag1 = stats::lag(df_adjts[,"PriceIndexGrowthSA"], -1),
PriceIndexGrowthLag2 = stats::lag(df_adjts[,"PriceIndexGrowthSA"], -2),
HousingStartGrowthLag1 = stats::lag(df_adjts[,"HousingStartGrowth"], -1),
HousingStartGrowthLag2 = stats::lag(df_adjts[,"HousingStartGrowth"], -2),
HousingStartGrowthLag3 = stats::lag(df_adjts[,"HousingStartGrowth"], -3),
HousingStartGrowthLag4 = stats::lag(df_adjts[,"HousingStartGrowth"], -4),
HousingStartGrowthLag9 = stats::lag(df_adjts[,"HousingStartGrowth"], -9),
HousingStartGrowthLag10 = stats::lag(df_adjts[,"HousingStartGrowth"], -10),
HousingStartGrowthLag11 = stats::lag(df_adjts[,"HousingStartGrowth"], -11),
HousingStartGrowthLag12 = stats::lag(df_adjts[,"HousingStartGrowth"], -12)) %>%
`colnames<-`(c(colnames(df_adjts),
"PriceIndexGrowthLag1","PriceIndexGrowthLag2","HousingStartGrowthLag1",
"HousingStartGrowthLag2","HousingStartGrowthLag3","HousingStartGrowthLag4",
"HousingStartGrowthLag9","HousingStartGrowthLag10","HousingStartGrowthLag11","HousingStartGrowthLag12"))
ADL_traindata= window(ADL_alldata, end = c(2013,12))
ADL_testdata= window(ADL_alldata, start = c(2014,1))
### Estimate ADL Model
ADL <- lm(PriceIndexGrowthSA ~ PriceIndexGrowthLag1+PriceIndexGrowthLag2+
HousingStartGrowthLag1 + HousingStartGrowthLag2 + HousingStartGrowthLag3 + HousingStartGrowthLag4 +
HousingStartGrowthLag9 + HousingStartGrowthLag10 + HousingStartGrowthLag11+HousingStartGrowthLag12,
data = ADL_traindata)
summary(ADL)
Call:
lm(formula = PriceIndexGrowthSA ~ PriceIndexGrowthLag1 + PriceIndexGrowthLag2 +
HousingStartGrowthLag1 + HousingStartGrowthLag2 + HousingStartGrowthLag3 +
HousingStartGrowthLag4 + HousingStartGrowthLag9 + HousingStartGrowthLag10 +
HousingStartGrowthLag11 + HousingStartGrowthLag12, data = ADL_traindata)
Residuals:
Min 1Q Median 3Q Max
-0.56261 -0.08130 0.01041 0.09052 1.15859
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0221341 0.0123032 1.799 0.07302 .
PriceIndexGrowthLag1 1.2788235 0.0527992 24.221 < 2e-16 ***
PriceIndexGrowthLag2 -0.3817242 0.0522745 -7.302 2.56e-12 ***
HousingStartGrowthLag1 0.0021102 0.0009023 2.339 0.02001 *
HousingStartGrowthLag2 0.0025173 0.0008662 2.906 0.00393 **
HousingStartGrowthLag3 0.0004962 0.0008868 0.560 0.57620
HousingStartGrowthLag4 0.0009169 0.0008871 1.034 0.30215
HousingStartGrowthLag9 0.0022220 0.0008776 2.532 0.01186 *
HousingStartGrowthLag10 0.0010251 0.0008827 1.161 0.24647
HousingStartGrowthLag11 -0.0007733 0.0008658 -0.893 0.37248
HousingStartGrowthLag12 -0.0009246 0.0009003 -1.027 0.30524
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1946 on 300 degrees of freedom
Multiple R-squared: 0.8932, Adjusted R-squared: 0.8896
F-statistic: 250.8 on 10 and 300 DF, p-value: < 2.2e-16acf2(residuals(ADL), main = "ACF and PACF of ADL Model Residuals") 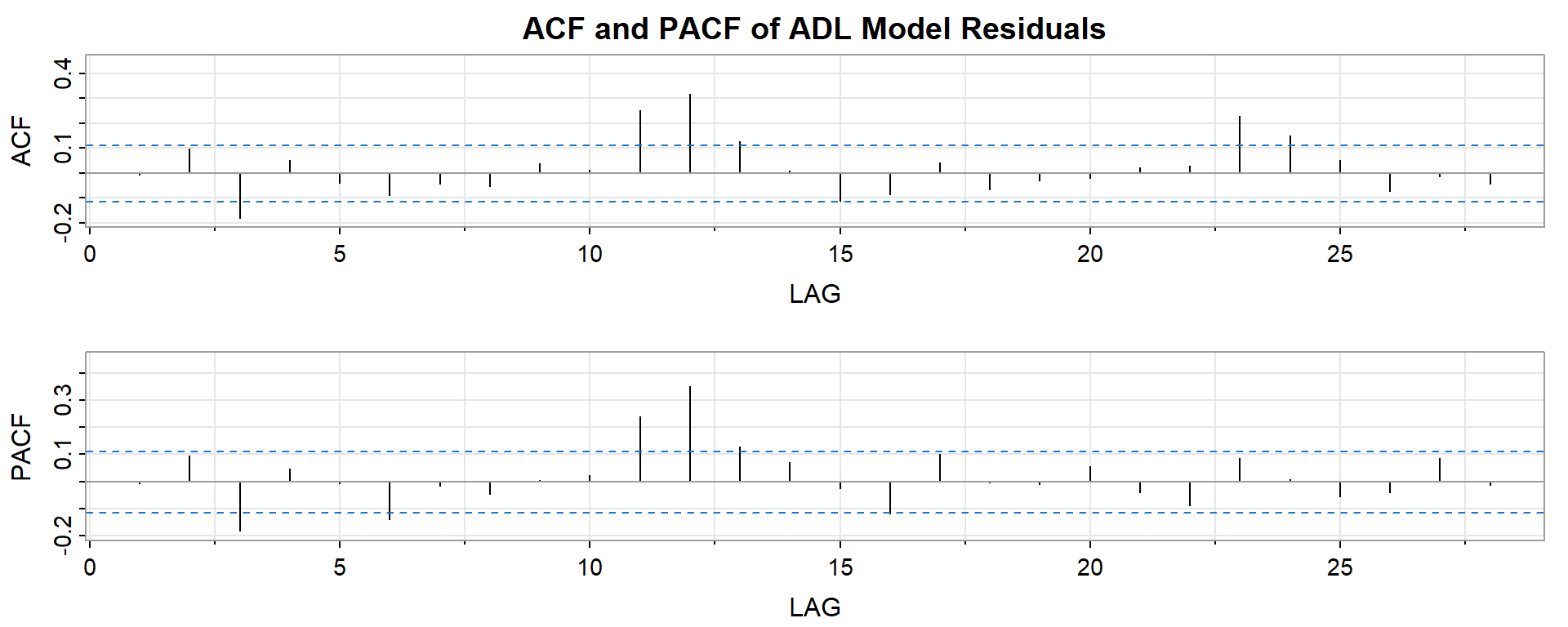
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
ACF -0.01 0.1 -0.18 0.05 -0.04 -0.09 -0.04 -0.05 0.04 0.01 0.25 0.32 0.13
PACF -0.01 0.1 -0.18 0.05 -0.01 -0.14 -0.02 -0.05 0.01 0.02 0.24 0.35 0.13
[,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF 0.01 -0.11 -0.09 0.04 -0.07 -0.03 -0.02 0.02 0.03 0.23 0.15 0.05
PACF 0.07 -0.03 -0.12 0.10 0.00 -0.01 0.06 -0.04 -0.09 0.09 0.01 -0.05
[,26] [,27] [,28]
ACF -0.07 -0.01 -0.05
PACF -0.04 0.09 -0.01Q: Interpret the residual correlogram.
A:
- The model residuals look nice and clean.
- There appears to be just a bit of temporal persistence left in the two month lag, but that’s minor
Q: Which coefficients are significant, and what do they mean?
A:
- The first 2 lags of prices seem significant. The first is >0, implying a rise in prices this month are associated with a rise in prices next month. The opposite is true for 2 months prior.
- Moreover, the first 2 lags of housing starts growth are significant and positive; i.e. if starts grow faster this month, prices are expected to rise next month.
Let’s compute the predicted value for our first observation in the training sample:
predict(ADL, newdata = head(ADL_testdata,1), interval = "confidence", level=0.95) fit lwr upr
1 0.3763717 0.3067218 0.4460216Q: What does fit, lwr, upr mean?
A:
- The “fit” is the prediction by the ``fitted’’ model
- the lwr and upr indicate the confidence bounds on that forecast.
Let’s compare to the observed value
window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014,1), end = c(2014,1))#observation Jan
2014 0.4292595Q: Comment on the quality of this single forecast.
A: - The forecast was .377 and the actual was .429. Somewhat close. - The actual is within the forecast confidence band, which is a good sign of fit. - We can quantify the quality of this forecast by various forecast evaluation criterion such as RMSFE (Root Mean Squared Forecast Errors). We’ll do so once we have a few models to compare.
Holt Winters
Holt Winters is a class of time series models that act entirely on the trend-cycle decomposition we highlighted earlier. It attempts to fit a model for the raw data by optimizing equations to represent three aspects of the additive time series: the level of the series, the trend of the series, and the seasonal component of the series.
plot(decompose(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)), type="additive"))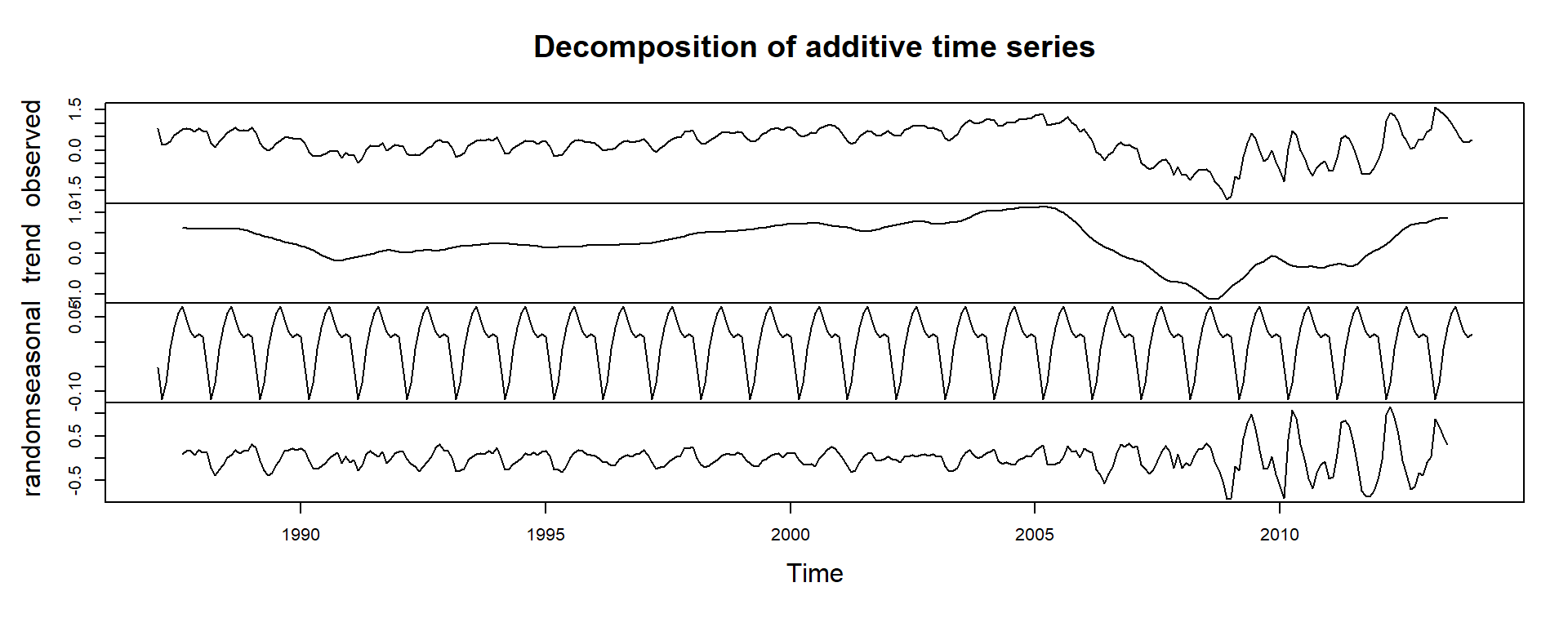
A preliminary diagnostic to determine of this class of model will be useful for you is whether the random component is very large in magnitude relative to the trend and seasonal. If so, the model likely won’t be very good.
Holt Winters is a flexible decomposition model well suited for forecasting. Within the R implementation there are several settings we can tune if desired:
• alpha: the “base value”. Higher alpha puts more weight on the most recent observations.
• beta: the “trend value”. Higher beta means the trend slope is more dependent on recent trend slopes.
• gamma: the “seasonal component”. Higher gamma puts more weighting on the most recent seasonal cycles.
### Fitting with Holt-Winters
HW1 <- HoltWinters(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)), seasonal = "additive")
### Plot fitted value of two models
{plot(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)),
ylab="Price Index Growth") # Visually evaluate the fits
lines(HW1$fitted[,1], lty=2, col="red")
legend("bottomleft",legend=c("Raw Data", "R Fit Holt-Winters"),
col=c("black","red"), lty=c(1,2), cex=0.8, box.lty=0)} 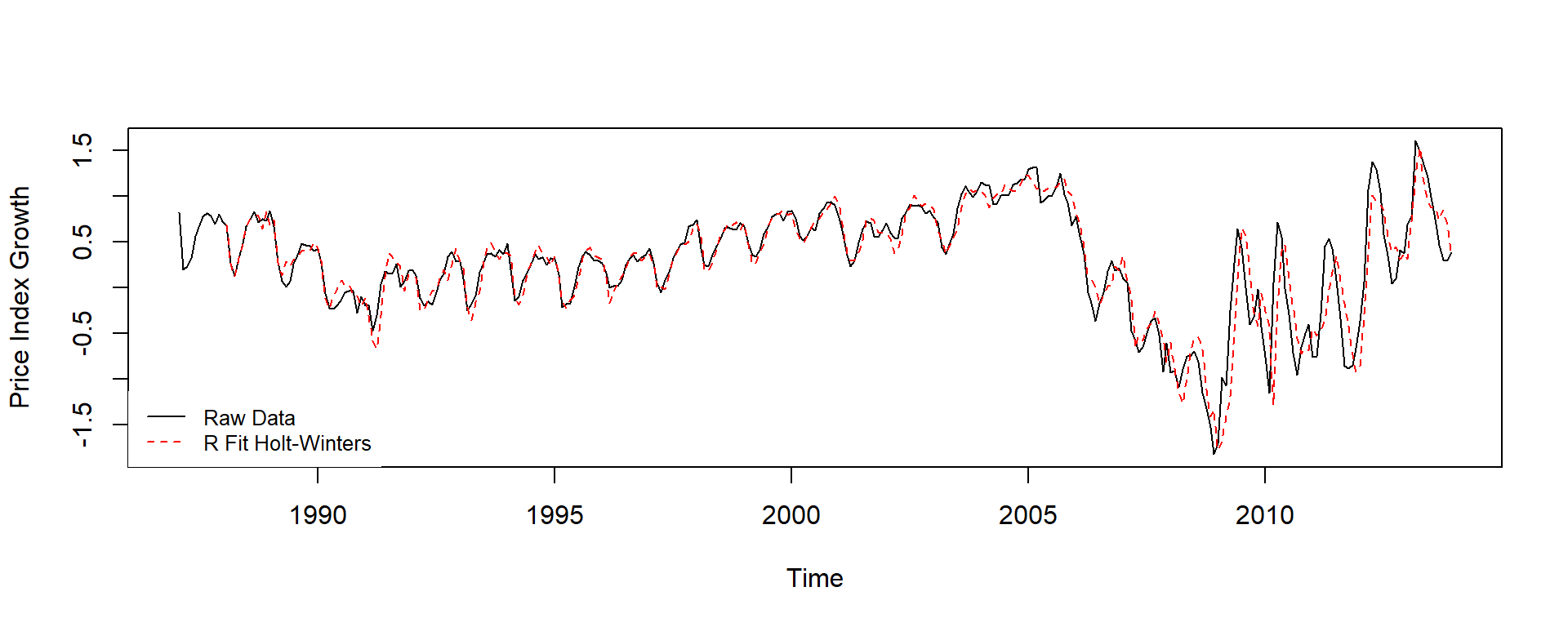
Q: Can you extract the optimal alpha, beta, gamma?
A:
optalpha = HW1$alpha
optbeta = HW1$beta
optgamma = HW1$gamma
rbind(optalpha, optbeta, optgamma) alpha
optalpha 0.7329786
optbeta 0.0000000
optgamma 1.0000000Tuning Holt Winters
Q: Can you rerun the model while giving the most recent observations only 10% of the optimal importance? Comment on your findings.
### Fitting with Holt-Winters
HW1 <- HoltWinters(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)), seasonal = "additive")
HW2 <- HoltWinters(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)), seasonal = "additive",alpha=optalpha*.1,beta=optbeta,gamma=optgamma)
### Plot fitted value of two models
{plot(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)),
ylab="Price Index Growth") # Visually evaluate the fits
lines(HW1$fitted[,1], lty=2, col="blue")
lines(HW2$fitted[,1], lty=2, col="red")
legend("bottomleft",legend=c("Raw Data", "Optimal Holt-Winters","Less Weight to Recent"),
col=c("black","blue", "red"), lty=c(1,2,2), cex=0.8, box.lty=0)} 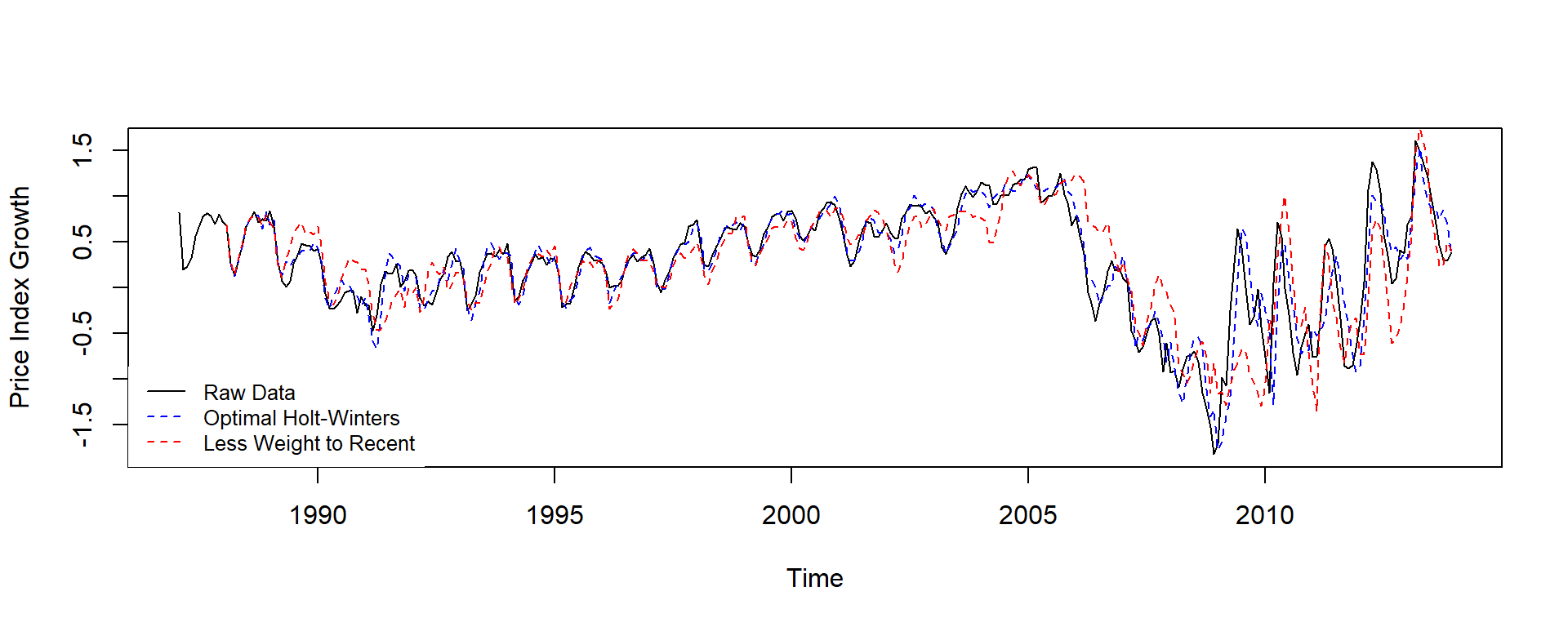
A: We can see the red line that doesn’t track the raw data as well. The model needs the recent temporal dynamics.
Forecasting with Holt Winters
Let’s predict one step ahead
predict(HW1, 1, prediction.interval = TRUE, level=0.95) fit upr lwr
Jan 2014 0.4149771 0.8716673 -0.04171311And compare to the observed value in the testing set
window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014,1), end = c(2014,1))#observation Jan
2014 0.4292595Q: Comment on the quality of this single forecast.
A:
- The forecast of .415 seems closer to the actual .429
- But the confidence bound seems wider.
ARMA
AutoRegressive Moving Average (ARMA) models are the bedrock of time series modeling. The basic idea is that every time series has its own temporal `fingerprint”. That fingerprint may depend upon its own past (AR), and/or the errors from that specification may also depend upon their own past (MA).
The further in the past that is relevant, the higher the “order” of the model. For instance, if housing prices in March depend upon housing prices in February and January, we have and order lag of 2, yielding AR(2).
Q: Why would the past values of housing prices (growth) be a useful feature for forecasting future housing prices?
A:
- There could be economic inertia. e.g. higher prices generate higher demand, which prompts higher prices. This could continue until supply catches up, which could take some time.
- There could be a latent driver that itself was temporal persistent. Being latent, we don’t have that driver.
- Thankfully, we can use a recursive substitution trick to capture the missing feature. (See lecture notes for details). Intuitively, …
- Suppose \(HousePrice_{t}=f(CPI_{t})\) and \(CPI_{t}=f(CPI_{t-1})\).
- This implies that \(HousePrice_{t}=f(CPI_{t-1})\), but if we don’t have CPI (in this silly example) this we can’t estimate this model.
- Thankfully, \(HousePrice_{t-1}=f(CPI_{t-1})\), so we can proxy the persistent latent driver CPI by using housing prices own temporal persistence \(HousePrice_{t-1}=f(HousePrice_{t-1})\)
- This is the foundation for ARMA-type models
Detect ARMA patterns
acf2(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)),
main = "ACF and PACF of Price Index Growth") 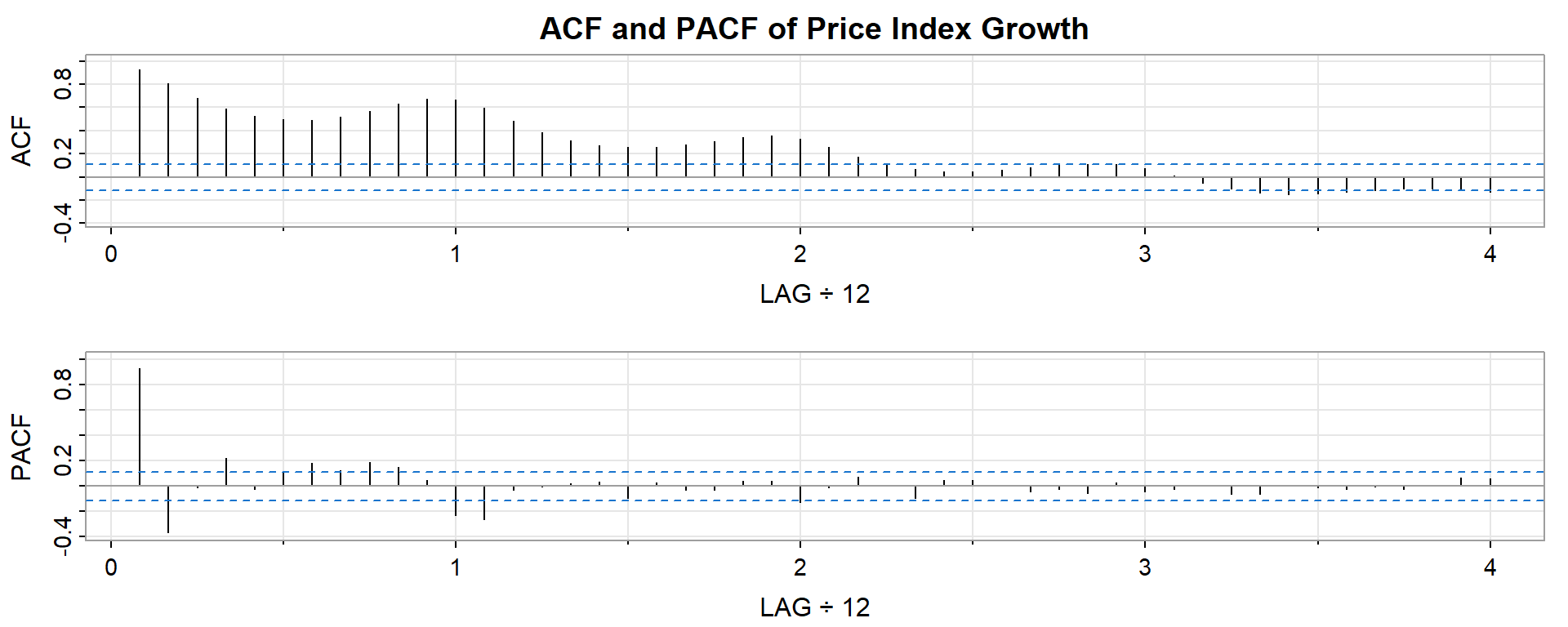
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
ACF 0.93 0.81 0.68 0.59 0.53 0.49 0.49 0.52 0.57 0.63 0.67 0.67 0.59
PACF 0.93 -0.37 -0.01 0.22 -0.02 0.11 0.18 0.12 0.18 0.15 0.05 -0.23 -0.26
[,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF 0.49 0.38 0.31 0.27 0.25 0.26 0.28 0.31 0.34 0.36 0.33 0.26
PACF -0.03 0.00 0.02 0.03 -0.10 0.03 -0.03 -0.03 0.04 0.04 -0.13 -0.02
[,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37]
ACF 0.18 0.11 0.07 0.04 0.04 0.06 0.08 0.10 0.11 0.11 0.07 0.01
PACF 0.07 0.00 -0.10 0.05 0.05 0.00 -0.05 -0.02 -0.06 0.03 -0.05 -0.03
[,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
ACF -0.05 -0.10 -0.13 -0.15 -0.15 -0.13 -0.11 -0.10 -0.11 -0.11 -0.13
PACF 0.01 -0.06 -0.06 0.01 -0.02 -0.03 -0.01 -0.03 0.00 0.07 0.06Q: What does the correlogram suggest about the persistence of the series?
A:
- The periodic swings in the ACF indicate some type of seasonality.
- The seasonal wave cresting roughly every twelve months is suggestive of an annual cycle.
- The spikes in the PACF suggest the possibility of a moving average MA component or order 1 or 2.
- Reading the correlogram for this purpose is usually referred to as the Box Jenkins approach. There are automatic search tools as well.
We can consider a 12month lag.
acf2(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12))%>%diff(lag = 12),
main = "ACF and PACF of Price Index Growth Diff 12", max.lag = 36)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
ACF 0.88 0.75 0.62 0.54 0.46 0.40 0.35 0.31 0.28 0.21 0.14 0.05 0.05
PACF 0.88 -0.12 -0.10 0.18 -0.08 0.04 0.03 -0.02 0.03 -0.20 -0.03 -0.08 0.30
[,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF 0.05 0.04 0.05 0.07 0.06 0.04 0.02 0.00 0.00 -0.01 -0.03 -0.04
PACF -0.09 -0.11 0.23 -0.03 -0.15 0.04 0.02 -0.01 -0.08 -0.01 -0.08 0.11
[,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36]
ACF -0.05 -0.03 -0.03 -0.03 -0.01 0.02 0.04 0.05 0.03 -0.01 -0.06
PACF -0.03 -0.01 0.09 0.04 -0.02 0.06 -0.01 -0.02 -0.14 -0.07 -0.16Q: What do you notice now?
A:
- Notice the seasonal wave of autocorrelation is gone.
- The remaining ACF decay and the single PACF indicate a remaining MA component.
Fit ARMA
AR(1)
We can fit an arma model by indicating the number of AR lags and how many MA lags. In this case, let’s first an AR(1,0,0) [often written as AR(1)] \(Price_{t} = \alpha + \beta Price_{t-1}+u_{t}\)
ARMA1 <- arima(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)),
order=c(1, 0, 0))
summary(ARMA1)
Call:
arima(x = window(df_adjts[, "PriceIndexGrowthSA"], end = c(2013, 12)), order = c(1,
0, 0))
Coefficients:
ar1 intercept
0.9261 0.3062
s.e. 0.0204 0.1569
sigma^2 estimated as 0.04677: log likelihood = 35.31, aic = -64.62
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set -0.002324743 0.2162601 0.1497961 86.92251 240.186 0.9945089
ACF1
Training set 0.3589425Q: Interpret the coefficients.
A:
- A 1 unit change in house price growth this month is associated with a .9261 unit increase in house price growth next month; i.e. this series is highly persistent.
- The intercept is the expected level of house price growth next month if prices didn’t grow at all this month.
ARMA(1,1)
Q: Can you specify and fit an ARMA(1,1)?
A: An ARMA(1,1) \(Price_{t} = \alpha + \beta Price_{t-1}+\gamma u_{t-1}+u_{t}\) is fit by
ARMA11 <- arima(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)),
order=c(1, 0, 1))
summary(ARMA11)
Call:
arima(x = window(df_adjts[, "PriceIndexGrowthSA"], end = c(2013, 12)), order = c(1,
0, 1))
Coefficients:
ar1 ma1 intercept
0.8904 0.3253 0.3054
s.e. 0.0259 0.0445 0.1329
sigma^2 estimated as 0.04098: log likelihood = 56.51, aic = -105.03
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set -0.002101107 0.2024426 0.1376628 64.54446 213.663 0.9139552
ACF1
Training set 0.06230336Seasonal ARMA
The ARMA structure is similar in spirit to our seasonal decomposition. They both use a series’ own past for modeling. We can combine the two with a Seasonal ARMA.
The c(p,d,q) elements in the ARMA function indicate the AR(p), MA(q), and the number (d) of differences. Similarly, seasonal components can be added analogously.
Consider an ARMA(1,0,0)(1,1,2)12 would be \(Price_{t}=\alpha+\beta_{1} Price_{t-1}+\beta_{2}Price_{t-12}+\gamma_{1}u_{t-12}+\gamma_{2}u_{t-24}+u_{t}\)
We could apply the seasonal ARMA directly to the Price Growth or even the Price series (with differencing), but we’ve been working with the SA price growth series, which has a meaningful interpretation for us, so we’ll proceed with that. Moreover, we did note that some seasonality did remain in that SA series, so we can attempt to address here.
ARMA11S <- arima(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)),
order=c(1, 0, 0), seasonal = list(order = c(0,1,2), period = 12))
summary(ARMA11S)
Call:
arima(x = window(df_adjts[, "PriceIndexGrowthSA"], end = c(2013, 12)), order = c(1,
0, 0), seasonal = list(order = c(0, 1, 2), period = 12))
Coefficients:
ar1 sma1 sma2
0.9249 -0.4962 -0.1052
s.e. 0.0219 0.0572 0.0607
sigma^2 estimated as 0.037: log likelihood = 68.31, aic = -128.63
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set -0.0005838792 0.1887389 0.1211854 -80.39207 261.5982 0.80456
ACF1
Training set 0.1694782Q: How can you use the aic to determine which model of the 3 we’ve estimated is preferred?
A:
- We want the smallest AIC (even the most negative)
- The Seasonal model appears to have the smallest -128.53
Auto Detect Lag Length
We can search among the evaluation criterion to find the optimal ARMA order.
ARIMA_auto <- auto.arima(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)), seasonal = TRUE)
summary(ARIMA_auto)Series: window(df_adjts[, "PriceIndexGrowthSA"], end = c(2013, 12))
ARIMA(2,0,2)(0,1,2)[12]
Coefficients:
ar1 ar2 ma1 ma2 sma1 sma2
0.2950 0.5145 0.8423 0.3395 -0.5528 -0.0992
s.e. 0.1615 0.1506 0.1558 0.0570 0.0601 0.0621
sigma^2 = 0.03434: log likelihood = 82.04
AIC=-150.08 AICc=-149.71 BIC=-123.9
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set -0.001809321 0.1800752 0.1149348 -96.67664 248.9524 0.3593316
ACF1
Training set -0.002539968Q: What is the optimal model order? Is there seasonality?
A:
- Here, R found an ARMA(2,0,2) with a 2 month seasonal component.
\(Price_{t}=\alpha+\beta_{1} Price_{t-1}+\beta_{2}Price_{t-2}+\gamma_{1}u_{t-1}+\gamma_{2}u_{t-2}+\gamma_{t-2}u_{t-12}+\gamma_{4}u_{t-24}+u_{t}\)
Post Estimation Diagnostics
Q: Is there remaining persistence?
Box.test(residuals(ARIMA_auto), type = "Ljung-Box")
Box-Ljung test
data: residuals(ARIMA_auto)
X-squared = 0.0021032, df = 1, p-value = 0.9634A:
- Recall the Lung Box Ho: No Autocorrelation in the errors.
- The very high pvalue suggests we fail to reject (ie no remaining serial correlation).
- Suggest we fit the series reasonably well with its own temporal dynamics
tsdisplay(residuals(ARIMA_auto), main='Model Residuals')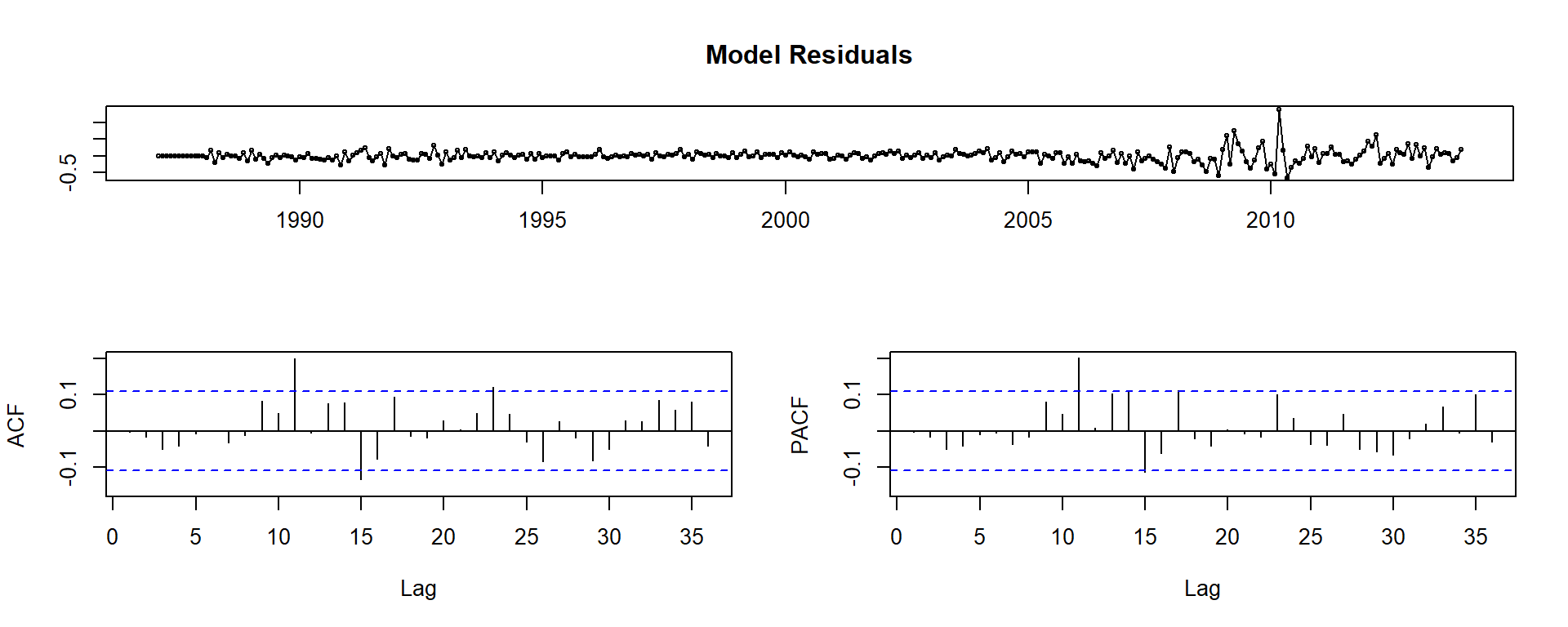
Q: What do the visuals here suggest about the model?
A:
- The visual diagnostics look pretty good.
- There are some annual spikes in the residuals
- There some issues with the model surrounding the GFC, which is not surprising.
Forecast Seasonal ARMA
Let’s use this ARMA model to predict one step ahead into the testing sample.
predict(ARIMA_auto, 1, prediction.interval = TRUE, level=0.95)$pred
Jan
2014 0.4872446
$se
Jan
2014 0.1853127And recall the observed value:
window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014,1), end = c(2014,1))#observation Jan
2014 0.4292595Q: Comment on the fit of this single forecast.
A:
- The fit is pretty good within relatively small standard error.
ARMA-GARCH
So far we’ve been focused on the price growth series. We can use ARMA to model or forecast that growth rate using its own temporal persistence.
The variability of the series may ALSO be temporally persistent.
Q: Why would the variability of house price growth be persistent? Why might that matter to us?
A:
- There could be an excluding driver that is swinging widely (e.g. lumber prices might be rising dramatically amid a sudden forest fire)
- This variability feed in directly to our confidence intervals.
- Fundamentally, that variability matters because it might impact decision making (e.g. if house prices are very variable, I may not know if now is a good time to invest in a home)
- Variability of time series is often itself autoregressive. So we have persistence in the “level” and “variance” of a series.
- By imposing an autoregressive structure onto the residuals of the model we can capture this characteristic.
Visualize GARCH Effects
Let’s visualize the variance of the model residuals.
residualSqr = residuals(ARIMA_auto)^2
tsdisplay(residualSqr, main = "Residual Square") 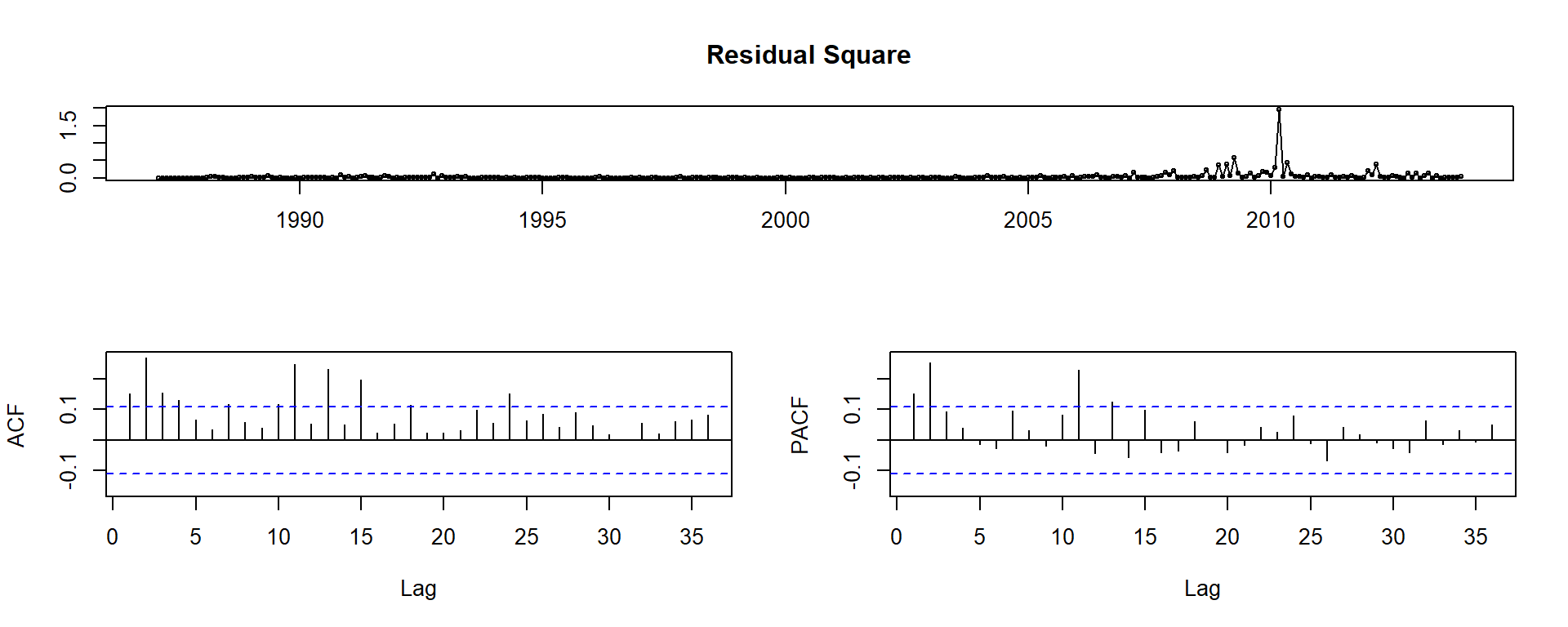
Q: What do these plots tell you?
A:
- Residual variance is proxied with the square of the residual
- Notice the persistence in the residual variance visa vis the ACF and PACF
- This is indicative of autoregressive volatility
- Notice also the spikes around the 2008 housing crisis, where uncertainty in the housing market was terribly high
Test for GARCH
We can test formally for (G)ARCH type effects with an Engle LM Test, which determines if the residual variance is indeed related to its own past.
Ho: No ARCH effects (white noise)
Ha: ARCH effects
library(FinTS)
ArchTest(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)), lags = 1, demean = TRUE)
ARCH LM-test; Null hypothesis: no ARCH effects
data: window(df_adjts[, "PriceIndexGrowthSA"], end = c(2013, 12))
Chi-squared = 229.53, df = 1, p-value < 2.2e-16Q: Interpret the test. What is the implication?
A:
- Notice that the small p value suggests we reject the null
- Implying we have ARCH-type effects
- Our model fit the ``level” of the series well, but something remains in the residual that is persistent.
Fitting an ARMA-GARCH
Augmenting our ARMA model with GARCH effects is easy in R. One limitation is the inability to forecast seasonal ARIMA-GARCH directly. So, we will demonstrate without seasonality.
Find approprate ARMA
ARIMA_nonseasonal<-auto.arima(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)),
seasonal = FALSE)
predict(ARIMA_nonseasonal,1, prediction.interval = TRUE, level=0.95)$pred
Jan
2014 0.5228583
$se
Jan
2014 0.1916733Fit ARMA-GARCH
We’ll use that optimal ARMA structure as the basis for the “mean” specification. We’ll also use the “workhorse” GARCH specification of a GARCH(1,1), which includes one lag of the variance of the errors (GARCH) as well as one lag of the model residuals (ARCH).
library(rugarch)
spec <- ugarchspec(variance.model=list(model="sGARCH", garchOrder=c(1,1)),
mean.model=list(include.mean = T, armaOrder=c(3,2)),
distribution.model="norm")
garch_fit <- ugarchfit(spec = spec, data = window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12)))
coef(garch_fit) mu ar1 ar2 ar3 ma1
0.3860651065 0.8161488423 -0.0932263725 0.1167177153 0.5461396966
ma2 omega alpha1 beta1
0.4710799169 0.0001839951 0.0756449565 0.9233550296 1-step Ahead ARMGARCH
ugarchforecast(fitORspec = garch_fit, n.ahead = 1)
*------------------------------------*
* GARCH Model Forecast *
*------------------------------------*
Model: sGARCH
Horizon: 1
Roll Steps: 0
Out of Sample: 0
0-roll forecast [T0=Dec 2013]:
Series Sigma
T+1 0.4292 0.2553For comparison, the observed testing sample observation was
window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014,1), end = c(2014,1))#observation Jan
2014 0.4292595Q: Comment on the quality of this single forecast.
A:
- Notice the fit is quite good.
NNET
A feed forward neural network with hidden layers can leverage lagged inputs for forecasting.
Fit the NNET
set.seed(123) # set random seed so that we can replicate the example
NNET <- nnetar(window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12))) Forecast the NNET
In the following, h = # of periods ahead to forecast. PI = True computes prediction intervals.
forecast(NNET, h = 1, PI=TRUE) Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 2014 0.4803274 0.2547668 0.7063296 0.1573808 0.8513227As a reminder
window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014,1), end = c(2014,1))#observation Jan
2014 0.4292595Q: Comment on the quality of this single forecast.
A: We get a great forecast with a modestly large confidence interval.
Random Forest
We must use caution when implementing a random forest model with time series data. As you may know, random forests are built by randomly selecting training data, upon which we estimate a regression tree. The process is repeated and then averaged together in an ensemble. The process of randomly selecting the observations to be used in the training set will disrupt the temporal persistence of the data. We need to ensure that the we are always using training data that occurred prior to the testing data. As such, we use forward-validation rather than k-fold cross validation.
Prep data
This step of prepping the data is sometimes called time embedding.
lag_order <- 12 # the lags number you want to include in your model
RF_data <- embed(df_adjts[,"PriceIndexGrowthSA"], lag_order + 1) %>% # embedding matrix
`colnames<-`(c("Raw",paste("Lag",1:lag_order, sep=''))) %>% ts(end = end(df_adjts), frequency = 12)
head(RF_data) Raw Lag1 Lag2 Lag3 Lag4 Lag5 Lag6
Feb 1988 0.6723727 0.7243508 0.8013131 0.6897618 0.7827210 0.8101789 0.7723659
Mar 1988 0.2644814 0.6723727 0.7243508 0.8013131 0.6897618 0.7827210 0.8101789
Apr 1988 0.1222968 0.2644814 0.6723727 0.7243508 0.8013131 0.6897618 0.7827210
May 1988 0.3186391 0.1222968 0.2644814 0.6723727 0.7243508 0.8013131 0.6897618
Jun 1988 0.4753510 0.3186391 0.1222968 0.2644814 0.6723727 0.7243508 0.8013131
Jul 1988 0.6671830 0.4753510 0.3186391 0.1222968 0.2644814 0.6723727 0.7243508
Lag7 Lag8 Lag9 Lag10 Lag11 Lag12
Feb 1988 0.6568641 0.5616372 0.3152181 0.2332973 0.1947912 0.8144339
Mar 1988 0.7723659 0.6568641 0.5616372 0.3152181 0.2332973 0.1947912
Apr 1988 0.8101789 0.7723659 0.6568641 0.5616372 0.3152181 0.2332973
May 1988 0.7827210 0.8101789 0.7723659 0.6568641 0.5616372 0.3152181
Jun 1988 0.6897618 0.7827210 0.8101789 0.7723659 0.6568641 0.5616372
Jul 1988 0.8013131 0.6897618 0.7827210 0.8101789 0.7723659 0.6568641Assign Train and Test Samples
RF_traindata <- window(RF_data, end = c(2013, 12))
RF_testdata <- window(RF_data, start = c(2014, 1))
y_train <- RF_traindata[, 1] # the target
X_train <- RF_traindata[, -1] # everything but the target
y_test <- RF_testdata[, 1]
X_test <- RF_testdata[, -1]Fit the Random Forest
library(randomForest)
set.seed(123) # set random seed so that we can replicate the example
RF_fit <- randomForest(X_train, y_train)Forecast the Random Forest
predict(RF_fit, head(X_test,1)) 1
0.3877122 And a reminder of the testing sample
window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014,1), end = c(2014,1)) Jan
2014 0.4292595Q: Comment on the quality of this single forecast.
A:
- We get a relatively accurate forecast.
- Unfortunately, a confidence interval isn’t provided natively.
Prophet
library(prophet)Prep Data
Prophet_traindata <- df_adj[1:323,]
Prophet_testdata <- df_adj[324:nrow(df_adj) ,]
df_prophet <- Prophet_traindata %>%
select(-HousingStartGrowth) %>%
rename(ds = Date) %>%
rename(y = PriceIndexGrowthSA)Forecast with Prophet
m <- prophet(df_prophet)
future <- make_future_dataframe(m, periods = 365, freq = "day", include_history = TRUE) # periods: Int number of periods to forecast forward.
forecast <- predict(m, future)
forecast ds trend additive_terms additive_terms_lower
1 1987-02-01 0.4040040 -0.0356416980 -0.0356416980
2 1987-03-01 0.4033586 -0.1186948625 -0.1186948625
3 1987-04-01 0.4026440 -0.0839145855 -0.0839145855
4 1987-05-01 0.4019524 -0.0201078993 -0.0201078993
5 1987-06-01 0.4012378 0.0291431734 0.0291431734
6 1987-07-01 0.4005463 0.0603561417 0.0603561417
7 1987-08-01 0.3998317 0.0661343534 0.0661343534
8 1987-09-01 0.3991171 0.0367875597 0.0367875597
9 1987-10-01 0.3984256 0.0130640560 0.0130640560
10 1987-11-01 0.3977110 0.0034683558 0.0034683558
11 1987-12-01 0.3970194 0.0167275567 0.0167275567
12 1988-01-01 0.3963048 0.0074538087 0.0074538087
13 1988-02-01 0.3955902 -0.0332346345 -0.0332346345
14 1988-03-01 0.3949217 -0.1094975179 -0.1094975179
15 1988-04-01 0.3942071 -0.0839114120 -0.0839114120
16 1988-05-01 0.3935156 -0.0202721392 -0.0202721392
17 1988-06-01 0.3928010 0.0275172532 0.0275172532
18 1988-07-01 0.3921095 0.0606205145 0.0606205145
19 1988-08-01 0.3913949 0.0668280996 0.0668280996
20 1988-09-01 0.3906803 0.0362205138 0.0362205138
21 1988-10-01 0.3899887 0.0142850189 0.0142850189
22 1988-11-01 0.3892741 0.0063376405 0.0063376405
23 1988-12-01 0.3885826 0.0131455845 0.0131455845
24 1989-01-01 0.3878680 0.0056177785 0.0056177785
25 1989-02-01 0.3871534 -0.0406308126 -0.0406308126
26 1989-03-01 0.3865080 -0.1125675613 -0.1125675613
27 1989-04-01 0.3857934 -0.0839678813 -0.0839678813
28 1989-05-01 0.3851018 -0.0202353637 -0.0202353637
29 1989-06-01 0.3843872 0.0280641464 0.0280641464
30 1989-07-01 0.3836957 0.0605569983 0.0605569983
31 1989-08-01 0.3829811 0.0666136819 0.0666136819
32 1989-09-01 0.3822665 0.0364169327 0.0364169327
33 1989-10-01 0.3815749 0.0138795813 0.0138795813
34 1989-11-01 0.3808603 0.0053483991 0.0053483991
35 1989-12-01 0.3801688 0.0143158624 0.0143158624
36 1990-01-01 0.3794542 0.0062331805 0.0062331805
37 1990-02-01 0.3787396 -0.0381076441 -0.0381076441
38 1990-03-01 0.3780942 -0.1156345445 -0.1156345445
39 1990-04-01 0.3773796 -0.0839690399 -0.0839690399
40 1990-05-01 0.3766880 -0.0201802758 -0.0201802758
41 1990-06-01 0.3759734 0.0286065568 0.0286065568
42 1990-07-01 0.3752819 0.0604689709 0.0604689709
43 1990-08-01 0.3745673 0.0663822973 0.0663822973
44 1990-09-01 0.3738527 0.0366058158 0.0366058158
45 1990-10-01 0.3731612 0.0134722674 0.0134722674
46 1990-11-01 0.3724466 0.0043916557 0.0043916557
47 1990-12-01 0.3717550 0.0155103422 0.0155103422
48 1991-01-01 0.3710404 0.0068456549 0.0068456549
49 1991-02-01 0.3703258 -0.0356416980 -0.0356416980
50 1991-03-01 0.3696804 -0.1186948625 -0.1186948625
51 1991-04-01 0.3689658 -0.0839145855 -0.0839145855
52 1991-05-01 0.3682742 -0.0201078993 -0.0201078993
53 1991-06-01 0.3675597 0.0291431734 0.0291431734
54 1991-07-01 0.3668681 0.0603561417 0.0603561417
55 1991-08-01 0.3661535 0.0661343534 0.0661343534
56 1991-09-01 0.3654389 0.0367875597 0.0367875597
57 1991-10-01 0.3647474 0.0130640560 0.0130640560
58 1991-11-01 0.3640328 0.0034683558 0.0034683558
59 1991-12-01 0.3633412 0.0167275567 0.0167275567
60 1992-01-01 0.3626266 0.0074538087 0.0074538087
61 1992-02-01 0.3619120 -0.0332346345 -0.0332346345
62 1992-03-01 0.3612435 -0.1094975179 -0.1094975179
63 1992-04-01 0.3605290 -0.0839114120 -0.0839114120
64 1992-05-01 0.3598374 -0.0202721392 -0.0202721392
65 1992-06-01 0.3591228 0.0275172532 0.0275172532
66 1992-07-01 0.3584313 0.0606205145 0.0606205145
67 1992-08-01 0.3577167 0.0668280996 0.0668280996
68 1992-09-01 0.3570021 0.0362205138 0.0362205138
69 1992-10-01 0.3563105 0.0142850189 0.0142850189
70 1992-11-01 0.3555959 0.0063376405 0.0063376405
71 1992-12-01 0.3549044 0.0131455845 0.0131455845
72 1993-01-01 0.3541898 0.0056177785 0.0056177785
73 1993-02-01 0.3534752 -0.0406308126 -0.0406308126
74 1993-03-01 0.3528298 -0.1125675613 -0.1125675613
75 1993-04-01 0.3521152 -0.0839678813 -0.0839678813
76 1993-05-01 0.3514236 -0.0202353637 -0.0202353637
77 1993-06-01 0.3507090 0.0280641464 0.0280641464
78 1993-07-01 0.3500175 0.0605569983 0.0605569983
79 1993-08-01 0.3493029 0.0666136819 0.0666136819
80 1993-09-01 0.3485883 0.0364169327 0.0364169327
81 1993-10-01 0.3478967 0.0138795813 0.0138795813
82 1993-11-01 0.3471822 0.0053483991 0.0053483991
83 1993-12-01 0.3464906 0.0143158624 0.0143158624
84 1994-01-01 0.3457760 0.0062331805 0.0062331805
85 1994-02-01 0.3450614 -0.0381076441 -0.0381076441
86 1994-03-01 0.3444160 -0.1156345445 -0.1156345445
87 1994-04-01 0.3437014 -0.0839690399 -0.0839690399
88 1994-05-01 0.3430098 -0.0201802758 -0.0201802758
89 1994-06-01 0.3422952 0.0286065568 0.0286065568
90 1994-07-01 0.3416037 0.0604689709 0.0604689709
91 1994-08-01 0.3408891 0.0663822973 0.0663822973
92 1994-09-01 0.3401745 0.0366058158 0.0366058158
93 1994-10-01 0.3394830 0.0134722674 0.0134722674
94 1994-11-01 0.3387684 0.0043916557 0.0043916557
95 1994-12-01 0.3380768 0.0155103422 0.0155103422
96 1995-01-01 0.3373622 0.0068456549 0.0068456549
97 1995-02-01 0.3366476 -0.0356416980 -0.0356416980
98 1995-03-01 0.3360022 -0.1186948625 -0.1186948625
99 1995-04-01 0.3352876 -0.0839145855 -0.0839145855
100 1995-05-01 0.3345961 -0.0201078993 -0.0201078993
101 1995-06-01 0.3338815 0.0291431734 0.0291431734
102 1995-07-01 0.3331899 0.0603561417 0.0603561417
103 1995-08-01 0.3324753 0.0661343534 0.0661343534
104 1995-09-01 0.3317607 0.0367875597 0.0367875597
105 1995-10-01 0.3310692 0.0130640560 0.0130640560
106 1995-11-01 0.3303546 0.0034683558 0.0034683558
107 1995-12-01 0.3296630 0.0167275567 0.0167275567
108 1996-01-01 0.3289484 0.0074538087 0.0074538087
109 1996-02-01 0.3282338 -0.0332346345 -0.0332346345
110 1996-03-01 0.3275654 -0.1094975179 -0.1094975179
111 1996-04-01 0.3268508 -0.0839114120 -0.0839114120
112 1996-05-01 0.3261592 -0.0202721392 -0.0202721392
113 1996-06-01 0.3254446 0.0275172532 0.0275172532
114 1996-07-01 0.3247531 0.0606205145 0.0606205145
115 1996-08-01 0.3240384 0.0668280996 0.0668280996
116 1996-09-01 0.3233238 0.0362205138 0.0362205138
117 1996-10-01 0.3226322 0.0142850189 0.0142850189
118 1996-11-01 0.3219176 0.0063376405 0.0063376405
119 1996-12-01 0.3212260 0.0131455845 0.0131455845
120 1997-01-01 0.3205114 0.0056177785 0.0056177785
121 1997-02-01 0.3197968 -0.0406308126 -0.0406308126
122 1997-03-01 0.3191513 -0.1125675613 -0.1125675613
123 1997-04-01 0.3184367 -0.0839678813 -0.0839678813
124 1997-05-01 0.3177451 -0.0202353637 -0.0202353637
125 1997-06-01 0.3170300 0.0280641464 0.0280641464
126 1997-07-01 0.3163380 0.0605569983 0.0605569983
127 1997-08-01 0.3156229 0.0666136819 0.0666136819
128 1997-09-01 0.3149078 0.0364169327 0.0364169327
129 1997-10-01 0.3142158 0.0138795813 0.0138795813
130 1997-11-01 0.3135007 0.0053483991 0.0053483991
131 1997-12-01 0.3128087 0.0143158624 0.0143158624
132 1998-01-01 0.3120937 0.0062331805 0.0062331805
133 1998-02-01 0.3113786 -0.0381076441 -0.0381076441
134 1998-03-01 0.3107327 -0.1156345445 -0.1156345445
135 1998-04-01 0.3100176 -0.0839690399 -0.0839690399
136 1998-05-01 0.3093252 -0.0201802758 -0.0201802758
137 1998-06-01 0.3086098 0.0286065568 0.0286065568
138 1998-07-01 0.3079174 0.0604689709 0.0604689709
139 1998-08-01 0.3072019 0.0663822973 0.0663822973
140 1998-09-01 0.3064865 0.0366058158 0.0366058158
141 1998-10-01 0.3057941 0.0134722674 0.0134722674
142 1998-11-01 0.3050786 0.0043916557 0.0043916557
143 1998-12-01 0.3043862 0.0155103422 0.0155103422
144 1999-01-01 0.3036707 0.0068456549 0.0068456549
145 1999-02-01 0.3029553 -0.0356416980 -0.0356416980
146 1999-03-01 0.3023030 -0.1186948625 -0.1186948625
147 1999-04-01 0.3015809 -0.0839145855 -0.0839145855
148 1999-05-01 0.3008820 -0.0201078993 -0.0201078993
149 1999-06-01 0.3001599 0.0291431734 0.0291431734
150 1999-07-01 0.2994611 0.0603561417 0.0603561417
151 1999-08-01 0.2987389 0.0661343534 0.0661343534
152 1999-09-01 0.2980168 0.0367875597 0.0367875597
153 1999-10-01 0.2973179 0.0130640560 0.0130640560
154 1999-11-01 0.2965958 0.0034683558 0.0034683558
155 1999-12-01 0.2958970 0.0167275567 0.0167275567
156 2000-01-01 0.2951661 0.0074538087 0.0074538087
157 2000-02-01 0.2944352 -0.0332346345 -0.0332346345
158 2000-03-01 0.2937515 -0.1094975179 -0.1094975179
159 2000-04-01 0.2930207 -0.0839114120 -0.0839114120
160 2000-05-01 0.2923134 -0.0202721392 -0.0202721392
161 2000-06-01 0.2915825 0.0275172532 0.0275172532
162 2000-07-01 0.2908752 0.0606205145 0.0606205145
163 2000-08-01 0.2901444 0.0668280996 0.0668280996
164 2000-09-01 0.2894135 0.0362205138 0.0362205138
165 2000-10-01 0.2887062 0.0142850189 0.0142850189
166 2000-11-01 0.2879708 0.0063376405 0.0063376405
167 2000-12-01 0.2872590 0.0131455845 0.0131455845
168 2001-01-01 0.2865235 0.0056177785 0.0056177785
169 2001-02-01 0.2857881 -0.0406308126 -0.0406308126
170 2001-03-01 0.2851238 -0.1125675613 -0.1125675613
171 2001-04-01 0.2843883 -0.0839678813 -0.0839678813
172 2001-05-01 0.2836766 -0.0202353637 -0.0202353637
173 2001-06-01 0.2829411 0.0280641464 0.0280641464
174 2001-07-01 0.2822294 0.0605569983 0.0605569983
175 2001-08-01 0.2814939 0.0666136819 0.0666136819
176 2001-09-01 0.2807584 0.0364169327 0.0364169327
177 2001-10-01 0.2800416 0.0138795813 0.0138795813
178 2001-11-01 0.2793009 0.0053483991 0.0053483991
179 2001-12-01 0.2785841 0.0143158624 0.0143158624
180 2002-01-01 0.2778434 0.0062331805 0.0062331805
181 2002-02-01 0.2771027 -0.0381076441 -0.0381076441
182 2002-03-01 0.2764336 -0.1156345445 -0.1156345445
183 2002-04-01 0.2756929 -0.0839690399 -0.0839690399
184 2002-05-01 0.2749761 -0.0201802758 -0.0201802758
185 2002-06-01 0.2742354 0.0286065568 0.0286065568
186 2002-07-01 0.2735186 0.0604689709 0.0604689709
187 2002-08-01 0.2727619 0.0663822973 0.0663822973
188 2002-09-01 0.2720052 0.0366058158 0.0366058158
189 2002-10-01 0.2712729 0.0134722674 0.0134722674
190 2002-11-01 0.2705162 0.0043916557 0.0043916557
191 2002-12-01 0.2697839 0.0155103422 0.0155103422
192 2003-01-01 0.2690272 0.0068456549 0.0068456549
193 2003-02-01 0.2682705 -0.0356416980 -0.0356416980
194 2003-03-01 0.2675870 -0.1186948625 -0.1186948625
195 2003-04-01 0.2668303 -0.0839145855 -0.0839145855
196 2003-05-01 0.2660981 -0.0201078993 -0.0201078993
197 2003-06-01 0.2653114 0.0291431734 0.0291431734
198 2003-07-01 0.2645501 0.0603561417 0.0603561417
199 2003-08-01 0.2637634 0.0661343534 0.0661343534
200 2003-09-01 0.2629768 0.0367875597 0.0367875597
201 2003-10-01 0.2622155 0.0130640560 0.0130640560
202 2003-11-01 0.2614288 0.0034683558 0.0034683558
203 2003-12-01 0.2606676 0.0167275567 0.0167275567
204 2004-01-01 0.2598809 0.0074538087 0.0074538087
205 2004-02-01 0.2590942 -0.0332346345 -0.0332346345
206 2004-03-01 0.2583583 -0.1094975179 -0.1094975179
207 2004-04-01 0.2575717 -0.0839114120 -0.0839114120
208 2004-05-01 0.2568059 -0.0202721392 -0.0202721392
209 2004-06-01 0.2560145 0.0275172532 0.0275172532
210 2004-07-01 0.2552487 0.0606205145 0.0606205145
211 2004-08-01 0.2544574 0.0668280996 0.0668280996
212 2004-09-01 0.2536661 0.0362205138 0.0362205138
213 2004-10-01 0.2529003 0.0142850189 0.0142850189
214 2004-11-01 0.2521089 0.0063376405 0.0063376405
215 2004-12-01 0.2513431 0.0131455845 0.0131455845
216 2005-01-01 0.2505518 0.0056177785 0.0056177785
217 2005-02-01 0.2497604 -0.0406308126 -0.0406308126
218 2005-03-01 0.2490421 -0.1125675613 -0.1125675613
219 2005-04-01 0.2482468 -0.0839678813 -0.0839678813
220 2005-05-01 0.2474772 -0.0202353637 -0.0202353637
221 2005-06-01 0.2466819 0.0280641464 0.0280641464
222 2005-07-01 0.2459123 0.0605569983 0.0605569983
223 2005-08-01 0.2451170 0.0666136819 0.0666136819
224 2005-09-01 0.2443217 0.0364169327 0.0364169327
225 2005-10-01 0.2435521 0.0138795813 0.0138795813
226 2005-11-01 0.2427568 0.0053483991 0.0053483991
227 2005-12-01 0.2419872 0.0143158624 0.0143158624
228 2006-01-01 0.2411918 0.0062331805 0.0062331805
229 2006-02-01 0.2403964 -0.0381076441 -0.0381076441
230 2006-03-01 0.2396779 -0.1156345445 -0.1156345445
231 2006-04-01 0.2388826 -0.0839690399 -0.0839690399
232 2006-05-01 0.2381128 -0.0201802758 -0.0201802758
233 2006-06-01 0.2373174 0.0286065568 0.0286065568
234 2006-07-01 0.2365477 0.0604689709 0.0604689709
235 2006-08-01 0.2357523 0.0663822973 0.0663822973
236 2006-09-01 0.2349569 0.0366058158 0.0366058158
237 2006-10-01 0.2341872 0.0134722674 0.0134722674
238 2006-11-01 0.2333918 0.0043916557 0.0043916557
239 2006-12-01 0.2326220 0.0155103422 0.0155103422
240 2007-01-01 0.2318267 0.0068456549 0.0068456549
241 2007-02-01 0.2310313 -0.0356416980 -0.0356416980
242 2007-03-01 0.2303128 -0.1186948625 -0.1186948625
243 2007-04-01 0.2295175 -0.0839145855 -0.0839145855
244 2007-05-01 0.2287477 -0.0201078993 -0.0201078993
245 2007-06-01 0.2279523 0.0291431734 0.0291431734
246 2007-07-01 0.2271826 0.0603561417 0.0603561417
247 2007-08-01 0.2263872 0.0661343534 0.0661343534
248 2007-09-01 0.2255918 0.0367875597 0.0367875597
249 2007-10-01 0.2248221 0.0130640560 0.0130640560
250 2007-11-01 0.2240267 0.0034683558 0.0034683558
251 2007-12-01 0.2232569 0.0167275567 0.0167275567
252 2008-01-01 0.2224616 0.0074538087 0.0074538087
253 2008-02-01 0.2216662 -0.0332346345 -0.0332346345
254 2008-03-01 0.2209221 -0.1094975179 -0.1094975179
255 2008-04-01 0.2201267 -0.0839114120 -0.0839114120
256 2008-05-01 0.2193570 -0.0202721392 -0.0202721392
257 2008-06-01 0.2185616 0.0275172532 0.0275172532
258 2008-07-01 0.2177918 0.0606205145 0.0606205145
259 2008-08-01 0.2169964 0.0668280996 0.0668280996
260 2008-09-01 0.2162010 0.0362205138 0.0362205138
261 2008-10-01 0.2154313 0.0142850189 0.0142850189
262 2008-11-01 0.2146359 0.0063376405 0.0063376405
263 2008-12-01 0.2138662 0.0131455845 0.0131455845
264 2009-01-01 0.2130708 0.0056177785 0.0056177785
265 2009-02-01 0.2122754 -0.0406308126 -0.0406308126
266 2009-03-01 0.2115570 -0.1125675613 -0.1125675613
267 2009-04-01 0.2107616 -0.0839678813 -0.0839678813
268 2009-05-01 0.2099919 -0.0202353637 -0.0202353637
269 2009-06-01 0.2091965 0.0280641464 0.0280641464
270 2009-07-01 0.2084267 0.0605569983 0.0605569983
271 2009-08-01 0.2076313 0.0666136819 0.0666136819
272 2009-09-01 0.2068359 0.0364169327 0.0364169327
273 2009-10-01 0.2060662 0.0138795813 0.0138795813
274 2009-11-01 0.2052708 0.0053483991 0.0053483991
275 2009-12-01 0.2045011 0.0143158624 0.0143158624
276 2010-01-01 0.2037057 0.0062331805 0.0062331805
277 2010-02-01 0.2029103 -0.0381076441 -0.0381076441
278 2010-03-01 0.2021919 -0.1156345445 -0.1156345445
279 2010-04-01 0.2013965 -0.0839690399 -0.0839690399
280 2010-05-01 0.2006267 -0.0201802758 -0.0201802758
281 2010-06-01 0.1998314 0.0286065568 0.0286065568
282 2010-07-01 0.1990616 0.0604689709 0.0604689709
283 2010-08-01 0.1982662 0.0663822973 0.0663822973
284 2010-09-01 0.1974708 0.0366058158 0.0366058158
285 2010-10-01 0.1967011 0.0134722674 0.0134722674
286 2010-11-01 0.1959057 0.0043916557 0.0043916557
287 2010-12-01 0.1951360 0.0155103422 0.0155103422
288 2011-01-01 0.1943406 0.0068456549 0.0068456549
289 2011-02-01 0.1935452 -0.0356416980 -0.0356416980
290 2011-03-01 0.1928268 -0.1186948625 -0.1186948625
291 2011-04-01 0.1920314 -0.0839145855 -0.0839145855
292 2011-05-01 0.1912616 -0.0201078993 -0.0201078993
293 2011-06-01 0.1904662 0.0291431734 0.0291431734
294 2011-07-01 0.1896965 0.0603561417 0.0603561417
295 2011-08-01 0.1889011 0.0661343534 0.0661343534
296 2011-09-01 0.1881057 0.0367875597 0.0367875597
297 2011-10-01 0.1873360 0.0130640560 0.0130640560
298 2011-11-01 0.1865406 0.0034683558 0.0034683558
299 2011-12-01 0.1857709 0.0167275567 0.0167275567
300 2012-01-01 0.1849755 0.0074538087 0.0074538087
301 2012-02-01 0.1841801 -0.0332346345 -0.0332346345
302 2012-03-01 0.1834360 -0.1094975179 -0.1094975179
303 2012-04-01 0.1826406 -0.0839114120 -0.0839114120
304 2012-05-01 0.1818709 -0.0202721392 -0.0202721392
305 2012-06-01 0.1810755 0.0275172532 0.0275172532
306 2012-07-01 0.1803058 0.0606205145 0.0606205145
307 2012-08-01 0.1795104 0.0668280996 0.0668280996
308 2012-09-01 0.1787150 0.0362205138 0.0362205138
309 2012-10-01 0.1779452 0.0142850189 0.0142850189
310 2012-11-01 0.1771498 0.0063376405 0.0063376405
311 2012-12-01 0.1763801 0.0131455845 0.0131455845
312 2013-01-01 0.1755847 0.0056177785 0.0056177785
313 2013-02-01 0.1747893 -0.0406308126 -0.0406308126
314 2013-03-01 0.1740709 -0.1125675613 -0.1125675613
315 2013-04-01 0.1732755 -0.0839678813 -0.0839678813
316 2013-05-01 0.1725058 -0.0202353637 -0.0202353637
317 2013-06-01 0.1717104 0.0280641464 0.0280641464
318 2013-07-01 0.1709406 0.0605569983 0.0605569983
319 2013-08-01 0.1701453 0.0666136819 0.0666136819
320 2013-09-01 0.1693499 0.0364169327 0.0364169327
321 2013-10-01 0.1685801 0.0138795813 0.0138795813
322 2013-11-01 0.1677847 0.0053483991 0.0053483991
323 2013-12-01 0.1670150 0.0143158624 0.0143158624
324 2013-12-02 0.1669893 0.0097938977 0.0097938977
325 2013-12-03 0.1669637 0.0057438420 0.0057438420
326 2013-12-04 0.1669380 0.0022368374 0.0022368374
327 2013-12-05 0.1669124 -0.0006722205 -0.0006722205
328 2013-12-06 0.1668867 -0.0029459602 -0.0029459602
329 2013-12-07 0.1668611 -0.0045653078 -0.0045653078
330 2013-12-08 0.1668354 -0.0055297348 -0.0055297348
331 2013-12-09 0.1668097 -0.0058569734 -0.0058569734
332 2013-12-10 0.1667841 -0.0055822085 -0.0055822085
333 2013-12-11 0.1667584 -0.0047567706 -0.0047567706
334 2013-12-12 0.1667328 -0.0034463678 -0.0034463678
335 2013-12-13 0.1667071 -0.0017289095 -0.0017289095
336 2013-12-14 0.1666815 0.0003080125 0.0003080125
337 2013-12-15 0.1666558 0.0025699130 0.0025699130
338 2013-12-16 0.1666301 0.0049583870 0.0049583870
339 2013-12-17 0.1666045 0.0073741811 0.0073741811
340 2013-12-18 0.1665788 0.0097202697 0.0097202697
341 2013-12-19 0.1665532 0.0119048436 0.0119048436
342 2013-12-20 0.1665275 0.0138441212 0.0138441212
343 2013-12-21 0.1665018 0.0154648967 0.0154648967
344 2013-12-22 0.1664762 0.0167067475 0.0167067475
345 2013-12-23 0.1664505 0.0175238316 0.0175238316
346 2013-12-24 0.1664249 0.0178862212 0.0178862212
347 2013-12-25 0.1663992 0.0177807266 0.0177807266
348 2013-12-26 0.1663736 0.0172111854 0.0172111854
349 2013-12-27 0.1663479 0.0161982033 0.0161982033
350 2013-12-28 0.1663222 0.0147783524 0.0147783524
351 2013-12-29 0.1662966 0.0130028463 0.0130028463
352 2013-12-30 0.1662709 0.0109357306 0.0109357306
353 2013-12-31 0.1662453 0.0086516389 0.0086516389
354 2014-01-01 0.1662196 0.0062331805 0.0062331805
355 2014-01-02 0.1661940 0.0037680361 0.0037680361
356 2014-01-03 0.1661683 0.0013458487 0.0013458487
357 2014-01-04 0.1661426 -0.0009449970 -0.0009449970
358 2014-01-05 0.1661170 -0.0030206093 -0.0030206093
359 2014-01-06 0.1660913 -0.0048047364 -0.0048047364
360 2014-01-07 0.1660657 -0.0062317303 -0.0062317303
361 2014-01-08 0.1660400 -0.0072492306 -0.0072492306
362 2014-01-09 0.1660143 -0.0078204824 -0.0078204824
363 2014-01-10 0.1659887 -0.0079262115 -0.0079262115
364 2014-01-11 0.1659630 -0.0075659894 -0.0075659894
365 2014-01-12 0.1659374 -0.0067590385 -0.0067590385
366 2014-01-13 0.1659117 -0.0055444409 -0.0055444409
367 2014-01-14 0.1658861 -0.0039807321 -0.0039807321
368 2014-01-15 0.1658604 -0.0021448791 -0.0021448791
369 2014-01-16 0.1658347 -0.0001306592 -0.0001306592
370 2014-01-17 0.1658091 0.0019535261 0.0019535261
371 2014-01-18 0.1657834 0.0039873491 0.0039873491
372 2014-01-19 0.1657578 0.0058417007 0.0058417007
373 2014-01-20 0.1657321 0.0073821993 0.0073821993
374 2014-01-21 0.1657065 0.0084729711 0.0084729711
375 2014-01-22 0.1656808 0.0089806008 0.0089806008
376 2014-01-23 0.1656551 0.0087781417 0.0087781417
377 2014-01-24 0.1656295 0.0077490755 0.0077490755
378 2014-01-25 0.1656038 0.0057911067 0.0057911067
379 2014-01-26 0.1655782 0.0028196833 0.0028196833
380 2014-01-27 0.1655525 -0.0012288609 -0.0012288609
381 2014-01-28 0.1655268 -0.0063946379 -0.0063946379
382 2014-01-29 0.1655012 -0.0126920941 -0.0126920941
383 2014-01-30 0.1654755 -0.0201085262 -0.0201085262
384 2014-01-31 0.1654499 -0.0286032763 -0.0286032763
385 2014-02-01 0.1654242 -0.0381076441 -0.0381076441
386 2014-02-02 0.1653986 -0.0485255308 -0.0485255308
387 2014-02-03 0.1653729 -0.0597348122 -0.0597348122
388 2014-02-04 0.1653472 -0.0715894189 -0.0715894189
389 2014-02-05 0.1653216 -0.0839220801 -0.0839220801
390 2014-02-06 0.1652959 -0.0965476714 -0.0965476714
391 2014-02-07 0.1652703 -0.1092670889 -0.1092670889
392 2014-02-08 0.1652446 -0.1218715561 -0.1218715561
393 2014-02-09 0.1652190 -0.1341472607 -0.1341472607
394 2014-02-10 0.1651933 -0.1458802029 -0.1458802029
395 2014-02-11 0.1651676 -0.1568611375 -0.1568611375
396 2014-02-12 0.1651420 -0.1668904803 -0.1668904803
397 2014-02-13 0.1651163 -0.1757830560 -0.1757830560
398 2014-02-14 0.1650907 -0.1833725635 -0.1833725635
399 2014-02-15 0.1650650 -0.1895156431 -0.1895156431
400 2014-02-16 0.1650394 -0.1940954375 -0.1940954375
401 2014-02-17 0.1650137 -0.1970245542 -0.1970245542
402 2014-02-18 0.1649880 -0.1982473485 -0.1982473485
403 2014-02-19 0.1649624 -0.1977414655 -0.1977414655
404 2014-02-20 0.1649367 -0.1955185976 -0.1955185976
405 2014-02-21 0.1649111 -0.1916244351 -0.1916244351
406 2014-02-22 0.1648854 -0.1861378059 -0.1861378059
407 2014-02-23 0.1648597 -0.1791690250 -0.1791690250
408 2014-02-24 0.1648341 -0.1708574906 -0.1708574906
409 2014-02-25 0.1648084 -0.1613685865 -0.1613685865
410 2014-02-26 0.1647828 -0.1508899674 -0.1508899674
411 2014-02-27 0.1647571 -0.1396273173 -0.1396273173
412 2014-02-28 0.1647315 -0.1277996900 -0.1277996900
413 2014-03-01 0.1647058 -0.1156345445 -0.1156345445
414 2014-03-02 0.1646801 -0.1033626029 -0.1033626029
415 2014-03-03 0.1646545 -0.0912126558 -0.0912126558
416 2014-03-04 0.1646288 -0.0794064475 -0.0794064475
417 2014-03-05 0.1646032 -0.0681537660 -0.0681537660
418 2014-03-06 0.1645775 -0.0576478593 -0.0576478593
419 2014-03-07 0.1645519 -0.0480612910 -0.0480612910
420 2014-03-08 0.1645262 -0.0395423341 -0.0395423341
421 2014-03-09 0.1645005 -0.0322119896 -0.0322119896
422 2014-03-10 0.1644749 -0.0261616990 -0.0261616990
423 2014-03-11 0.1644492 -0.0214518011 -0.0214518011
424 2014-03-12 0.1644236 -0.0181107641 -0.0181107641
425 2014-03-13 0.1643979 -0.0161352044 -0.0161352044
426 2014-03-14 0.1643722 -0.0154906818 -0.0154906818
427 2014-03-15 0.1643466 -0.0161132408 -0.0161132408
428 2014-03-16 0.1643209 -0.0179116504 -0.0179116504
429 2014-03-17 0.1642953 -0.0207702755 -0.0207702755
430 2014-03-18 0.1642696 -0.0245524960 -0.0245524960
431 2014-03-19 0.1642440 -0.0291045799 -0.0291045799
432 2014-03-20 0.1642183 -0.0342599038 -0.0342599038
433 2014-03-21 0.1641926 -0.0398434042 -0.0398434042
434 2014-03-22 0.1641670 -0.0456761445 -0.0456761445
435 2014-03-23 0.1641413 -0.0515798738 -0.0515798738
436 2014-03-24 0.1641157 -0.0573814622 -0.0573814622
437 2014-03-25 0.1640900 -0.0629170960 -0.0629170960
438 2014-03-26 0.1640644 -0.0680361313 -0.0680361313
439 2014-03-27 0.1640387 -0.0726045070 -0.0726045070
440 2014-03-28 0.1640130 -0.0765076399 -0.0765076399
441 2014-03-29 0.1639874 -0.0796527327 -0.0796527327
442 2014-03-30 0.1639617 -0.0819704471 -0.0819704471
443 2014-03-31 0.1639361 -0.0834159098 -0.0834159098
444 2014-04-01 0.1639104 -0.0839690399 -0.0839690399
445 2014-04-02 0.1638847 -0.0836342014 -0.0836342014
446 2014-04-03 0.1638591 -0.0824392078 -0.0824392078
447 2014-04-04 0.1638334 -0.0804337169 -0.0804337169
448 2014-04-05 0.1638078 -0.0776870769 -0.0776870769
449 2014-04-06 0.1637821 -0.0742856923 -0.0742856923
450 2014-04-07 0.1637565 -0.0703299948 -0.0703299948
451 2014-04-08 0.1637308 -0.0659311117 -0.0659311117
452 2014-04-09 0.1637051 -0.0612073312 -0.0612073312
453 2014-04-10 0.1636795 -0.0562804689 -0.0562804689
454 2014-04-11 0.1636538 -0.0512722385 -0.0512722385
455 2014-04-12 0.1636282 -0.0463007305 -0.0463007305
456 2014-04-13 0.1636025 -0.0414770952 -0.0414770952
457 2014-04-14 0.1635769 -0.0369025199 -0.0369025199
458 2014-04-15 0.1635512 -0.0326655812 -0.0326655812
459 2014-04-16 0.1635255 -0.0288400379 -0.0288400379
460 2014-04-17 0.1634999 -0.0254831205 -0.0254831205
461 2014-04-18 0.1634742 -0.0226343543 -0.0226343543
462 2014-04-19 0.1634486 -0.0203149398 -0.0203149398
463 2014-04-20 0.1634229 -0.0185276957 -0.0185276957
464 2014-04-21 0.1633972 -0.0172575540 -0.0172575540
465 2014-04-22 0.1633716 -0.0164725828 -0.0164725828
466 2014-04-23 0.1633459 -0.0161254935 -0.0161254935
467 2014-04-24 0.1633203 -0.0161555800 -0.0161555800
468 2014-04-25 0.1632946 -0.0164910223 -0.0164910223
469 2014-04-26 0.1632690 -0.0170514801 -0.0170514801
470 2014-04-27 0.1632433 -0.0177508932 -0.0177508932
471 2014-04-28 0.1632176 -0.0185004003 -0.0185004003
472 2014-04-29 0.1631920 -0.0192112879 -0.0192112879
473 2014-04-30 0.1631663 -0.0197978789 -0.0197978789
474 2014-05-01 0.1631407 -0.0201802758 -0.0201802758
475 2014-05-02 0.1631150 -0.0202868780 -0.0202868780
476 2014-05-03 0.1630894 -0.0200565996 -0.0200565996
477 2014-05-04 0.1630637 -0.0194407278 -0.0194407278
478 2014-05-05 0.1630380 -0.0184043675 -0.0184043675
479 2014-05-06 0.1630124 -0.0169274378 -0.0169274378
480 2014-05-07 0.1629867 -0.0150051934 -0.0150051934
481 2014-05-08 0.1629611 -0.0126482637 -0.0126482637
482 2014-05-09 0.1629354 -0.0098822133 -0.0098822133
483 2014-05-10 0.1629098 -0.0067466436 -0.0067466436
484 2014-05-11 0.1628841 -0.0032938685 -0.0032938685
485 2014-05-12 0.1628584 0.0004127907 0.0004127907
486 2014-05-13 0.1628328 0.0043010353 0.0043010353
487 2014-05-14 0.1628071 0.0082918795 0.0082918795
488 2014-05-15 0.1627815 0.0123021272 0.0123021272
489 2014-05-16 0.1627558 0.0162469609 0.0162469609
490 2014-05-17 0.1627301 0.0200425603 0.0200425603
491 2014-05-18 0.1627045 0.0236086740 0.0236086740
492 2014-05-19 0.1626788 0.0268710650 0.0268710650
493 2014-05-20 0.1626532 0.0297637579 0.0297637579
494 2014-05-21 0.1626275 0.0322310229 0.0322310229
495 2014-05-22 0.1626019 0.0342290372 0.0342290372
496 2014-05-23 0.1625762 0.0357271781 0.0357271781
497 2014-05-24 0.1625505 0.0367089122 0.0367089122
498 2014-05-25 0.1625249 0.0371722560 0.0371722560
499 2014-05-26 0.1624992 0.0371297990 0.0371297990
500 2014-05-27 0.1624736 0.0366082921 0.0366082921
501 2014-05-28 0.1624479 0.0356478162 0.0356478162
502 2014-05-29 0.1624223 0.0343005606 0.0343005606
503 2014-05-30 0.1623966 0.0326292505 0.0326292505
504 2014-05-31 0.1623709 0.0307052723 0.0307052723
505 2014-06-01 0.1623453 0.0286065568 0.0286065568
506 2014-06-02 0.1623196 0.0264152844 0.0264152844
507 2014-06-03 0.1622940 0.0242154818 0.0242154818
508 2014-06-04 0.1622683 0.0220905831 0.0220905831
509 2014-06-05 0.1622426 0.0201210281 0.0201210281
510 2014-06-06 0.1622170 0.0183819674 0.0183819674
511 2014-06-07 0.1621913 0.0169411437 0.0169411437
512 2014-06-08 0.1621657 0.0158570079 0.0158570079
513 2014-06-09 0.1621400 0.0151771255 0.0151771255
514 2014-06-10 0.1621144 0.0149369168 0.0149369168
515 2014-06-11 0.1620887 0.0151587651 0.0151587651
516 2014-06-12 0.1620630 0.0158515160 0.0158515160
517 2014-06-13 0.1620374 0.0170103778 0.0170103778
518 2014-06-14 0.1620117 0.0186172227 0.0186172227
519 2014-06-15 0.1619861 0.0206412753 0.0206412753
520 2014-06-16 0.1619604 0.0230401640 0.0230401640
521 2014-06-17 0.1619348 0.0257612991 0.0257612991
522 2014-06-18 0.1619091 0.0287435353 0.0287435353
523 2014-06-19 0.1618834 0.0319190636 0.0319190636
524 2014-06-20 0.1618578 0.0352154759 0.0352154759
525 2014-06-21 0.1618321 0.0385579367 0.0385579367
526 2014-06-22 0.1618065 0.0418713986 0.0418713986
527 2014-06-23 0.1617808 0.0450827930 0.0450827930
528 2014-06-24 0.1617551 0.0481231319 0.0481231319
529 2014-06-25 0.1617295 0.0509294598 0.0509294598
530 2014-06-26 0.1617038 0.0534465976 0.0534465976
531 2014-06-27 0.1616782 0.0556286309 0.0556286309
532 2014-06-28 0.1616525 0.0574401005 0.0574401005
533 2014-06-29 0.1616269 0.0588568630 0.0588568630
534 2014-06-30 0.1616012 0.0598666009 0.0598666009
535 2014-07-01 0.1615755 0.0604689709 0.0604689709
536 2014-07-02 0.1615499 0.0606753904 0.0606753904
537 2014-07-03 0.1615242 0.0605084749 0.0605084749
538 2014-07-04 0.1614986 0.0600011464 0.0600011464
539 2014-07-05 0.1614729 0.0591954451 0.0591954451
540 2014-07-06 0.1614473 0.0581410846 0.0581410846
541 2014-07-07 0.1614216 0.0568937970 0.0568937970
542 2014-07-08 0.1613959 0.0555135223 0.0555135223
543 2014-07-09 0.1613703 0.0540624982 0.0540624982
544 2014-07-10 0.1613446 0.0526033104 0.0526033104
545 2014-07-11 0.1613190 0.0511969635 0.0511969635
546 2014-07-12 0.1612933 0.0499010308 0.0499010308
547 2014-07-13 0.1612677 0.0487679388 0.0487679388
548 2014-07-14 0.1612420 0.0478434363 0.0478434363
549 2014-07-15 0.1612163 0.0471652940 0.0471652940
550 2014-07-16 0.1611907 0.0467622691 0.0467622691
551 2014-07-17 0.1611650 0.0466533650 0.0466533650
552 2014-07-18 0.1611394 0.0468474037 0.0468474037
553 2014-07-19 0.1611137 0.0473429185 0.0473429185
554 2014-07-20 0.1610880 0.0481283687 0.0481283687
555 2014-07-21 0.1610624 0.0491826612 0.0491826612
556 2014-07-22 0.1610367 0.0504759608 0.0504759608
557 2014-07-23 0.1610111 0.0519707592 0.0519707592
558 2014-07-24 0.1609854 0.0536231645 0.0536231645
559 2014-07-25 0.1609598 0.0553843691 0.0553843691
560 2014-07-26 0.1609341 0.0572022455 0.0572022455
561 2014-07-27 0.1609084 0.0590230201 0.0590230201
562 2014-07-28 0.1608828 0.0607929689 0.0607929689
563 2014-07-29 0.1608571 0.0624600830 0.0624600830
564 2014-07-30 0.1608315 0.0639756499 0.0639756499
565 2014-07-31 0.1608058 0.0652957036 0.0652957036
566 2014-08-01 0.1607802 0.0663822973 0.0663822973
567 2014-08-02 0.1607545 0.0672045620 0.0672045620
568 2014-08-03 0.1607288 0.0677395196 0.0677395196
569 2014-08-04 0.1607032 0.0679726285 0.0679726285
570 2014-08-05 0.1606775 0.0678980473 0.0678980473
571 2014-08-06 0.1606519 0.0675186128 0.0675186128
572 2014-08-07 0.1606262 0.0668455368 0.0668455368
573 2014-08-08 0.1606005 0.0658978363 0.0658978363
574 2014-08-09 0.1605749 0.0647015175 0.0647015175
575 2014-08-10 0.1605492 0.0632885473 0.0632885473
576 2014-08-11 0.1605236 0.0616956450 0.0616956450
577 2014-08-12 0.1604979 0.0599629401 0.0599629401
578 2014-08-13 0.1604723 0.0581325402 0.0581325402
579 2014-08-14 0.1604466 0.0562470599 0.0562470599
580 2014-08-15 0.1604209 0.0543481583 0.0543481583
581 2014-08-16 0.1603953 0.0524751365 0.0524751365
582 2014-08-17 0.1603696 0.0506636402 0.0506636402
583 2014-08-18 0.1603440 0.0489445117 0.0489445117
584 2014-08-19 0.1603183 0.0473428278 0.0473428278
585 2014-08-20 0.1602927 0.0458771561 0.0458771561
586 2014-08-21 0.1602670 0.0445590527 0.0445590527
587 2014-08-22 0.1602413 0.0433928173 0.0433928173
588 2014-08-23 0.1602157 0.0423755127 0.0423755127
589 2014-08-24 0.1601900 0.0414972461 0.0414972461
590 2014-08-25 0.1601644 0.0407417027 0.0407417027
591 2014-08-26 0.1601387 0.0400869097 0.0400869097
592 2014-08-27 0.1601130 0.0395062070 0.0395062070
593 2014-08-28 0.1600874 0.0389693869 0.0389693869
594 2014-08-29 0.1600617 0.0384439650 0.0384439650
595 2014-08-30 0.1600361 0.0378965377 0.0378965377
596 2014-08-31 0.1600104 0.0372941769 0.0372941769
597 2014-09-01 0.1599848 0.0366058158 0.0366058158
598 2014-09-02 0.1599591 0.0358035740 0.0358035740
599 2014-09-03 0.1599334 0.0348639767 0.0348639767
600 2014-09-04 0.1599078 0.0337690237 0.0337690237
601 2014-09-05 0.1598821 0.0325070686 0.0325070686
602 2014-09-06 0.1598565 0.0310734767 0.0310734767
603 2014-09-07 0.1598308 0.0294710346 0.0294710346
604 2014-09-08 0.1598052 0.0277100955 0.0277100955
605 2014-09-09 0.1597795 0.0258084501 0.0258084501
606 2014-09-10 0.1597538 0.0237909251 0.0237909251
607 2014-09-11 0.1597282 0.0216887184 0.0216887184
608 2014-09-12 0.1597025 0.0195384899 0.0195384899
609 2014-09-13 0.1596769 0.0173812348 0.0173812348
610 2014-09-14 0.1596512 0.0152609753 0.0152609753
611 2014-09-15 0.1596256 0.0132233114 0.0132233114
612 2014-09-16 0.1595999 0.0113138773 0.0113138773
613 2014-09-17 0.1595742 0.0095767557 0.0095767557
614 2014-09-18 0.1595486 0.0080529006 0.0080529006
615 2014-09-19 0.1595229 0.0067786248 0.0067786248
616 2014-09-20 0.1594973 0.0057842010 0.0057842010
617 2014-09-21 0.1594716 0.0050926296 0.0050926296
618 2014-09-22 0.1594459 0.0047186151 0.0047186151
619 2014-09-23 0.1594203 0.0046677912 0.0046677912
620 2014-09-24 0.1593946 0.0049362258 0.0049362258
621 2014-09-25 0.1593690 0.0055102291 0.0055102291
622 2014-09-26 0.1593433 0.0063664776 0.0063664776
623 2014-09-27 0.1593177 0.0074724579 0.0074724579
624 2014-09-28 0.1592920 0.0087872241 0.0087872241
625 2014-09-29 0.1592663 0.0102624514 0.0102624514
626 2014-09-30 0.1592407 0.0118437590 0.0118437590
627 2014-10-01 0.1592150 0.0134722674 0.0134722674
628 2014-10-02 0.1591894 0.0150863459 0.0150863459
629 2014-10-03 0.1591637 0.0166234984 0.0166234984
630 2014-10-04 0.1591381 0.0180223329 0.0180223329
631 2014-10-05 0.1591124 0.0192245539 0.0192245539
632 2014-10-06 0.1590867 0.0201769146 0.0201769146
633 2014-10-07 0.1590611 0.0208330695 0.0208330695
634 2014-10-08 0.1590354 0.0211552645 0.0211552645
635 2014-10-09 0.1590098 0.0211158093 0.0211158093
636 2014-10-10 0.1589841 0.0206982818 0.0206982818
637 2014-10-11 0.1589584 0.0198984196 0.0198984196
638 2014-10-12 0.1589328 0.0187246640 0.0187246640
639 2014-10-13 0.1589071 0.0171983323 0.0171983323
640 2014-10-14 0.1588815 0.0153534026 0.0153534026
641 2014-10-15 0.1588558 0.0132359096 0.0132359096
642 2014-10-16 0.1588302 0.0109029597 0.0109029597
643 2014-10-17 0.1588045 0.0084213862 0.0084213862
644 2014-10-18 0.1587788 0.0058660759 0.0058660759
645 2014-10-19 0.1587532 0.0033180099 0.0033180099
646 2014-10-20 0.1587275 0.0008620702 0.0008620702
647 2014-10-21 0.1587019 -0.0014153287 -0.0014153287
648 2014-10-22 0.1586762 -0.0034287175 -0.0034287175
649 2014-10-23 0.1586506 -0.0050960878 -0.0050960878
650 2014-10-24 0.1586249 -0.0063413743 -0.0063413743
651 2014-10-25 0.1585992 -0.0070968298 -0.0070968298
652 2014-10-26 0.1585736 -0.0073052214 -0.0073052214
653 2014-10-27 0.1585479 -0.0069217820 -0.0069217820
654 2014-10-28 0.1585223 -0.0059158544 -0.0059158544
655 2014-10-29 0.1584966 -0.0042721757 -0.0042721757
656 2014-10-30 0.1584709 -0.0019917584 -0.0019917584
657 2014-10-31 0.1584453 0.0009076652 0.0009076652
658 2014-11-01 0.1584196 0.0043916557 0.0043916557
659 2014-11-02 0.1583940 0.0084095428 0.0084095428
660 2014-11-03 0.1583683 0.0128953614 0.0128953614
661 2014-11-04 0.1583427 0.0177692278 0.0177692278
662 2014-11-05 0.1583170 0.0229391233 0.0229391233
663 2014-11-06 0.1582913 0.0283030431 0.0283030431
664 2014-11-07 0.1582657 0.0337514543 0.0337514543
665 2014-11-08 0.1582400 0.0391699992 0.0391699992
666 2014-11-09 0.1582144 0.0444423708 0.0444423708
667 2014-11-10 0.1581887 0.0494532841 0.0494532841
668 2014-11-11 0.1581631 0.0540914595 0.0540914595
669 2014-11-12 0.1581374 0.0582525370 0.0582525370
670 2014-11-13 0.1581117 0.0618418386 0.0618418386
671 2014-11-14 0.1580861 0.0647769010 0.0647769010
672 2014-11-15 0.1580604 0.0669897051 0.0669897051
673 2014-11-16 0.1580348 0.0684285394 0.0684285394
674 2014-11-17 0.1580091 0.0690594396 0.0690594396
675 2014-11-18 0.1579834 0.0688671642 0.0688671642
676 2014-11-19 0.1579578 0.0678556731 0.0678556731
677 2014-11-20 0.1579321 0.0660480935 0.0660480935
678 2014-11-21 0.1579065 0.0634861709 0.0634861709
679 2014-11-22 0.1578808 0.0602292165 0.0602292165
680 2014-11-23 0.1578552 0.0563525797 0.0563525797
681 2014-11-24 0.1578295 0.0519456827 0.0519456827
682 2014-11-25 0.1578038 0.0471096734 0.0471096734
683 2014-11-26 0.1577782 0.0419547590 0.0419547590
684 2014-11-27 0.1577525 0.0365972934 0.0365972934
685 2014-11-28 0.1577269 0.0311567007 0.0311567007
686 2014-11-29 0.1577012 0.0257523196 0.0257523196
687 2014-11-30 0.1576756 0.0205002574 0.0205002574
688 2014-12-01 0.1576499 0.0155103422 0.0155103422
additive_terms_upper yearly yearly_lower yearly_upper
1 -0.0356416980 -0.0356416980 -0.0356416980 -0.0356416980
2 -0.1186948625 -0.1186948625 -0.1186948625 -0.1186948625
3 -0.0839145855 -0.0839145855 -0.0839145855 -0.0839145855
4 -0.0201078993 -0.0201078993 -0.0201078993 -0.0201078993
5 0.0291431734 0.0291431734 0.0291431734 0.0291431734
6 0.0603561417 0.0603561417 0.0603561417 0.0603561417
7 0.0661343534 0.0661343534 0.0661343534 0.0661343534
8 0.0367875597 0.0367875597 0.0367875597 0.0367875597
9 0.0130640560 0.0130640560 0.0130640560 0.0130640560
10 0.0034683558 0.0034683558 0.0034683558 0.0034683558
11 0.0167275567 0.0167275567 0.0167275567 0.0167275567
12 0.0074538087 0.0074538087 0.0074538087 0.0074538087
13 -0.0332346345 -0.0332346345 -0.0332346345 -0.0332346345
14 -0.1094975179 -0.1094975179 -0.1094975179 -0.1094975179
15 -0.0839114120 -0.0839114120 -0.0839114120 -0.0839114120
16 -0.0202721392 -0.0202721392 -0.0202721392 -0.0202721392
17 0.0275172532 0.0275172532 0.0275172532 0.0275172532
18 0.0606205145 0.0606205145 0.0606205145 0.0606205145
19 0.0668280996 0.0668280996 0.0668280996 0.0668280996
20 0.0362205138 0.0362205138 0.0362205138 0.0362205138
21 0.0142850189 0.0142850189 0.0142850189 0.0142850189
22 0.0063376405 0.0063376405 0.0063376405 0.0063376405
23 0.0131455845 0.0131455845 0.0131455845 0.0131455845
24 0.0056177785 0.0056177785 0.0056177785 0.0056177785
25 -0.0406308126 -0.0406308126 -0.0406308126 -0.0406308126
26 -0.1125675613 -0.1125675613 -0.1125675613 -0.1125675613
27 -0.0839678813 -0.0839678813 -0.0839678813 -0.0839678813
28 -0.0202353637 -0.0202353637 -0.0202353637 -0.0202353637
29 0.0280641464 0.0280641464 0.0280641464 0.0280641464
30 0.0605569983 0.0605569983 0.0605569983 0.0605569983
31 0.0666136819 0.0666136819 0.0666136819 0.0666136819
32 0.0364169327 0.0364169327 0.0364169327 0.0364169327
33 0.0138795813 0.0138795813 0.0138795813 0.0138795813
34 0.0053483991 0.0053483991 0.0053483991 0.0053483991
35 0.0143158624 0.0143158624 0.0143158624 0.0143158624
36 0.0062331805 0.0062331805 0.0062331805 0.0062331805
37 -0.0381076441 -0.0381076441 -0.0381076441 -0.0381076441
38 -0.1156345445 -0.1156345445 -0.1156345445 -0.1156345445
39 -0.0839690399 -0.0839690399 -0.0839690399 -0.0839690399
40 -0.0201802758 -0.0201802758 -0.0201802758 -0.0201802758
41 0.0286065568 0.0286065568 0.0286065568 0.0286065568
42 0.0604689709 0.0604689709 0.0604689709 0.0604689709
43 0.0663822973 0.0663822973 0.0663822973 0.0663822973
44 0.0366058158 0.0366058158 0.0366058158 0.0366058158
45 0.0134722674 0.0134722674 0.0134722674 0.0134722674
46 0.0043916557 0.0043916557 0.0043916557 0.0043916557
47 0.0155103422 0.0155103422 0.0155103422 0.0155103422
48 0.0068456549 0.0068456549 0.0068456549 0.0068456549
49 -0.0356416980 -0.0356416980 -0.0356416980 -0.0356416980
50 -0.1186948625 -0.1186948625 -0.1186948625 -0.1186948625
51 -0.0839145855 -0.0839145855 -0.0839145855 -0.0839145855
52 -0.0201078993 -0.0201078993 -0.0201078993 -0.0201078993
53 0.0291431734 0.0291431734 0.0291431734 0.0291431734
54 0.0603561417 0.0603561417 0.0603561417 0.0603561417
55 0.0661343534 0.0661343534 0.0661343534 0.0661343534
56 0.0367875597 0.0367875597 0.0367875597 0.0367875597
57 0.0130640560 0.0130640560 0.0130640560 0.0130640560
58 0.0034683558 0.0034683558 0.0034683558 0.0034683558
59 0.0167275567 0.0167275567 0.0167275567 0.0167275567
60 0.0074538087 0.0074538087 0.0074538087 0.0074538087
61 -0.0332346345 -0.0332346345 -0.0332346345 -0.0332346345
62 -0.1094975179 -0.1094975179 -0.1094975179 -0.1094975179
63 -0.0839114120 -0.0839114120 -0.0839114120 -0.0839114120
64 -0.0202721392 -0.0202721392 -0.0202721392 -0.0202721392
65 0.0275172532 0.0275172532 0.0275172532 0.0275172532
66 0.0606205145 0.0606205145 0.0606205145 0.0606205145
67 0.0668280996 0.0668280996 0.0668280996 0.0668280996
68 0.0362205138 0.0362205138 0.0362205138 0.0362205138
69 0.0142850189 0.0142850189 0.0142850189 0.0142850189
70 0.0063376405 0.0063376405 0.0063376405 0.0063376405
71 0.0131455845 0.0131455845 0.0131455845 0.0131455845
72 0.0056177785 0.0056177785 0.0056177785 0.0056177785
73 -0.0406308126 -0.0406308126 -0.0406308126 -0.0406308126
74 -0.1125675613 -0.1125675613 -0.1125675613 -0.1125675613
75 -0.0839678813 -0.0839678813 -0.0839678813 -0.0839678813
76 -0.0202353637 -0.0202353637 -0.0202353637 -0.0202353637
77 0.0280641464 0.0280641464 0.0280641464 0.0280641464
78 0.0605569983 0.0605569983 0.0605569983 0.0605569983
79 0.0666136819 0.0666136819 0.0666136819 0.0666136819
80 0.0364169327 0.0364169327 0.0364169327 0.0364169327
81 0.0138795813 0.0138795813 0.0138795813 0.0138795813
82 0.0053483991 0.0053483991 0.0053483991 0.0053483991
83 0.0143158624 0.0143158624 0.0143158624 0.0143158624
84 0.0062331805 0.0062331805 0.0062331805 0.0062331805
85 -0.0381076441 -0.0381076441 -0.0381076441 -0.0381076441
86 -0.1156345445 -0.1156345445 -0.1156345445 -0.1156345445
87 -0.0839690399 -0.0839690399 -0.0839690399 -0.0839690399
88 -0.0201802758 -0.0201802758 -0.0201802758 -0.0201802758
89 0.0286065568 0.0286065568 0.0286065568 0.0286065568
90 0.0604689709 0.0604689709 0.0604689709 0.0604689709
91 0.0663822973 0.0663822973 0.0663822973 0.0663822973
92 0.0366058158 0.0366058158 0.0366058158 0.0366058158
93 0.0134722674 0.0134722674 0.0134722674 0.0134722674
94 0.0043916557 0.0043916557 0.0043916557 0.0043916557
95 0.0155103422 0.0155103422 0.0155103422 0.0155103422
96 0.0068456549 0.0068456549 0.0068456549 0.0068456549
97 -0.0356416980 -0.0356416980 -0.0356416980 -0.0356416980
98 -0.1186948625 -0.1186948625 -0.1186948625 -0.1186948625
99 -0.0839145855 -0.0839145855 -0.0839145855 -0.0839145855
100 -0.0201078993 -0.0201078993 -0.0201078993 -0.0201078993
101 0.0291431734 0.0291431734 0.0291431734 0.0291431734
102 0.0603561417 0.0603561417 0.0603561417 0.0603561417
103 0.0661343534 0.0661343534 0.0661343534 0.0661343534
104 0.0367875597 0.0367875597 0.0367875597 0.0367875597
105 0.0130640560 0.0130640560 0.0130640560 0.0130640560
106 0.0034683558 0.0034683558 0.0034683558 0.0034683558
107 0.0167275567 0.0167275567 0.0167275567 0.0167275567
108 0.0074538087 0.0074538087 0.0074538087 0.0074538087
109 -0.0332346345 -0.0332346345 -0.0332346345 -0.0332346345
110 -0.1094975179 -0.1094975179 -0.1094975179 -0.1094975179
111 -0.0839114120 -0.0839114120 -0.0839114120 -0.0839114120
112 -0.0202721392 -0.0202721392 -0.0202721392 -0.0202721392
113 0.0275172532 0.0275172532 0.0275172532 0.0275172532
114 0.0606205145 0.0606205145 0.0606205145 0.0606205145
115 0.0668280996 0.0668280996 0.0668280996 0.0668280996
116 0.0362205138 0.0362205138 0.0362205138 0.0362205138
117 0.0142850189 0.0142850189 0.0142850189 0.0142850189
118 0.0063376405 0.0063376405 0.0063376405 0.0063376405
119 0.0131455845 0.0131455845 0.0131455845 0.0131455845
120 0.0056177785 0.0056177785 0.0056177785 0.0056177785
121 -0.0406308126 -0.0406308126 -0.0406308126 -0.0406308126
122 -0.1125675613 -0.1125675613 -0.1125675613 -0.1125675613
123 -0.0839678813 -0.0839678813 -0.0839678813 -0.0839678813
124 -0.0202353637 -0.0202353637 -0.0202353637 -0.0202353637
125 0.0280641464 0.0280641464 0.0280641464 0.0280641464
126 0.0605569983 0.0605569983 0.0605569983 0.0605569983
127 0.0666136819 0.0666136819 0.0666136819 0.0666136819
128 0.0364169327 0.0364169327 0.0364169327 0.0364169327
129 0.0138795813 0.0138795813 0.0138795813 0.0138795813
130 0.0053483991 0.0053483991 0.0053483991 0.0053483991
131 0.0143158624 0.0143158624 0.0143158624 0.0143158624
132 0.0062331805 0.0062331805 0.0062331805 0.0062331805
133 -0.0381076441 -0.0381076441 -0.0381076441 -0.0381076441
134 -0.1156345445 -0.1156345445 -0.1156345445 -0.1156345445
135 -0.0839690399 -0.0839690399 -0.0839690399 -0.0839690399
136 -0.0201802758 -0.0201802758 -0.0201802758 -0.0201802758
137 0.0286065568 0.0286065568 0.0286065568 0.0286065568
138 0.0604689709 0.0604689709 0.0604689709 0.0604689709
139 0.0663822973 0.0663822973 0.0663822973 0.0663822973
140 0.0366058158 0.0366058158 0.0366058158 0.0366058158
141 0.0134722674 0.0134722674 0.0134722674 0.0134722674
142 0.0043916557 0.0043916557 0.0043916557 0.0043916557
143 0.0155103422 0.0155103422 0.0155103422 0.0155103422
144 0.0068456549 0.0068456549 0.0068456549 0.0068456549
145 -0.0356416980 -0.0356416980 -0.0356416980 -0.0356416980
146 -0.1186948625 -0.1186948625 -0.1186948625 -0.1186948625
147 -0.0839145855 -0.0839145855 -0.0839145855 -0.0839145855
148 -0.0201078993 -0.0201078993 -0.0201078993 -0.0201078993
149 0.0291431734 0.0291431734 0.0291431734 0.0291431734
150 0.0603561417 0.0603561417 0.0603561417 0.0603561417
151 0.0661343534 0.0661343534 0.0661343534 0.0661343534
152 0.0367875597 0.0367875597 0.0367875597 0.0367875597
153 0.0130640560 0.0130640560 0.0130640560 0.0130640560
154 0.0034683558 0.0034683558 0.0034683558 0.0034683558
155 0.0167275567 0.0167275567 0.0167275567 0.0167275567
156 0.0074538087 0.0074538087 0.0074538087 0.0074538087
157 -0.0332346345 -0.0332346345 -0.0332346345 -0.0332346345
158 -0.1094975179 -0.1094975179 -0.1094975179 -0.1094975179
159 -0.0839114120 -0.0839114120 -0.0839114120 -0.0839114120
160 -0.0202721392 -0.0202721392 -0.0202721392 -0.0202721392
161 0.0275172532 0.0275172532 0.0275172532 0.0275172532
162 0.0606205145 0.0606205145 0.0606205145 0.0606205145
163 0.0668280996 0.0668280996 0.0668280996 0.0668280996
164 0.0362205138 0.0362205138 0.0362205138 0.0362205138
165 0.0142850189 0.0142850189 0.0142850189 0.0142850189
166 0.0063376405 0.0063376405 0.0063376405 0.0063376405
167 0.0131455845 0.0131455845 0.0131455845 0.0131455845
168 0.0056177785 0.0056177785 0.0056177785 0.0056177785
169 -0.0406308126 -0.0406308126 -0.0406308126 -0.0406308126
170 -0.1125675613 -0.1125675613 -0.1125675613 -0.1125675613
171 -0.0839678813 -0.0839678813 -0.0839678813 -0.0839678813
172 -0.0202353637 -0.0202353637 -0.0202353637 -0.0202353637
173 0.0280641464 0.0280641464 0.0280641464 0.0280641464
174 0.0605569983 0.0605569983 0.0605569983 0.0605569983
175 0.0666136819 0.0666136819 0.0666136819 0.0666136819
176 0.0364169327 0.0364169327 0.0364169327 0.0364169327
177 0.0138795813 0.0138795813 0.0138795813 0.0138795813
178 0.0053483991 0.0053483991 0.0053483991 0.0053483991
179 0.0143158624 0.0143158624 0.0143158624 0.0143158624
180 0.0062331805 0.0062331805 0.0062331805 0.0062331805
181 -0.0381076441 -0.0381076441 -0.0381076441 -0.0381076441
182 -0.1156345445 -0.1156345445 -0.1156345445 -0.1156345445
183 -0.0839690399 -0.0839690399 -0.0839690399 -0.0839690399
184 -0.0201802758 -0.0201802758 -0.0201802758 -0.0201802758
185 0.0286065568 0.0286065568 0.0286065568 0.0286065568
186 0.0604689709 0.0604689709 0.0604689709 0.0604689709
187 0.0663822973 0.0663822973 0.0663822973 0.0663822973
188 0.0366058158 0.0366058158 0.0366058158 0.0366058158
189 0.0134722674 0.0134722674 0.0134722674 0.0134722674
190 0.0043916557 0.0043916557 0.0043916557 0.0043916557
191 0.0155103422 0.0155103422 0.0155103422 0.0155103422
192 0.0068456549 0.0068456549 0.0068456549 0.0068456549
193 -0.0356416980 -0.0356416980 -0.0356416980 -0.0356416980
194 -0.1186948625 -0.1186948625 -0.1186948625 -0.1186948625
195 -0.0839145855 -0.0839145855 -0.0839145855 -0.0839145855
196 -0.0201078993 -0.0201078993 -0.0201078993 -0.0201078993
197 0.0291431734 0.0291431734 0.0291431734 0.0291431734
198 0.0603561417 0.0603561417 0.0603561417 0.0603561417
199 0.0661343534 0.0661343534 0.0661343534 0.0661343534
200 0.0367875597 0.0367875597 0.0367875597 0.0367875597
201 0.0130640560 0.0130640560 0.0130640560 0.0130640560
202 0.0034683558 0.0034683558 0.0034683558 0.0034683558
203 0.0167275567 0.0167275567 0.0167275567 0.0167275567
204 0.0074538087 0.0074538087 0.0074538087 0.0074538087
205 -0.0332346345 -0.0332346345 -0.0332346345 -0.0332346345
206 -0.1094975179 -0.1094975179 -0.1094975179 -0.1094975179
207 -0.0839114120 -0.0839114120 -0.0839114120 -0.0839114120
208 -0.0202721392 -0.0202721392 -0.0202721392 -0.0202721392
209 0.0275172532 0.0275172532 0.0275172532 0.0275172532
210 0.0606205145 0.0606205145 0.0606205145 0.0606205145
211 0.0668280996 0.0668280996 0.0668280996 0.0668280996
212 0.0362205138 0.0362205138 0.0362205138 0.0362205138
213 0.0142850189 0.0142850189 0.0142850189 0.0142850189
214 0.0063376405 0.0063376405 0.0063376405 0.0063376405
215 0.0131455845 0.0131455845 0.0131455845 0.0131455845
216 0.0056177785 0.0056177785 0.0056177785 0.0056177785
217 -0.0406308126 -0.0406308126 -0.0406308126 -0.0406308126
218 -0.1125675613 -0.1125675613 -0.1125675613 -0.1125675613
219 -0.0839678813 -0.0839678813 -0.0839678813 -0.0839678813
220 -0.0202353637 -0.0202353637 -0.0202353637 -0.0202353637
221 0.0280641464 0.0280641464 0.0280641464 0.0280641464
222 0.0605569983 0.0605569983 0.0605569983 0.0605569983
223 0.0666136819 0.0666136819 0.0666136819 0.0666136819
224 0.0364169327 0.0364169327 0.0364169327 0.0364169327
225 0.0138795813 0.0138795813 0.0138795813 0.0138795813
226 0.0053483991 0.0053483991 0.0053483991 0.0053483991
227 0.0143158624 0.0143158624 0.0143158624 0.0143158624
228 0.0062331805 0.0062331805 0.0062331805 0.0062331805
229 -0.0381076441 -0.0381076441 -0.0381076441 -0.0381076441
230 -0.1156345445 -0.1156345445 -0.1156345445 -0.1156345445
231 -0.0839690399 -0.0839690399 -0.0839690399 -0.0839690399
232 -0.0201802758 -0.0201802758 -0.0201802758 -0.0201802758
233 0.0286065568 0.0286065568 0.0286065568 0.0286065568
234 0.0604689709 0.0604689709 0.0604689709 0.0604689709
235 0.0663822973 0.0663822973 0.0663822973 0.0663822973
236 0.0366058158 0.0366058158 0.0366058158 0.0366058158
237 0.0134722674 0.0134722674 0.0134722674 0.0134722674
238 0.0043916557 0.0043916557 0.0043916557 0.0043916557
239 0.0155103422 0.0155103422 0.0155103422 0.0155103422
240 0.0068456549 0.0068456549 0.0068456549 0.0068456549
241 -0.0356416980 -0.0356416980 -0.0356416980 -0.0356416980
242 -0.1186948625 -0.1186948625 -0.1186948625 -0.1186948625
243 -0.0839145855 -0.0839145855 -0.0839145855 -0.0839145855
244 -0.0201078993 -0.0201078993 -0.0201078993 -0.0201078993
245 0.0291431734 0.0291431734 0.0291431734 0.0291431734
246 0.0603561417 0.0603561417 0.0603561417 0.0603561417
247 0.0661343534 0.0661343534 0.0661343534 0.0661343534
248 0.0367875597 0.0367875597 0.0367875597 0.0367875597
249 0.0130640560 0.0130640560 0.0130640560 0.0130640560
250 0.0034683558 0.0034683558 0.0034683558 0.0034683558
251 0.0167275567 0.0167275567 0.0167275567 0.0167275567
252 0.0074538087 0.0074538087 0.0074538087 0.0074538087
253 -0.0332346345 -0.0332346345 -0.0332346345 -0.0332346345
254 -0.1094975179 -0.1094975179 -0.1094975179 -0.1094975179
255 -0.0839114120 -0.0839114120 -0.0839114120 -0.0839114120
256 -0.0202721392 -0.0202721392 -0.0202721392 -0.0202721392
257 0.0275172532 0.0275172532 0.0275172532 0.0275172532
258 0.0606205145 0.0606205145 0.0606205145 0.0606205145
259 0.0668280996 0.0668280996 0.0668280996 0.0668280996
260 0.0362205138 0.0362205138 0.0362205138 0.0362205138
261 0.0142850189 0.0142850189 0.0142850189 0.0142850189
262 0.0063376405 0.0063376405 0.0063376405 0.0063376405
263 0.0131455845 0.0131455845 0.0131455845 0.0131455845
264 0.0056177785 0.0056177785 0.0056177785 0.0056177785
265 -0.0406308126 -0.0406308126 -0.0406308126 -0.0406308126
266 -0.1125675613 -0.1125675613 -0.1125675613 -0.1125675613
267 -0.0839678813 -0.0839678813 -0.0839678813 -0.0839678813
268 -0.0202353637 -0.0202353637 -0.0202353637 -0.0202353637
269 0.0280641464 0.0280641464 0.0280641464 0.0280641464
270 0.0605569983 0.0605569983 0.0605569983 0.0605569983
271 0.0666136819 0.0666136819 0.0666136819 0.0666136819
272 0.0364169327 0.0364169327 0.0364169327 0.0364169327
273 0.0138795813 0.0138795813 0.0138795813 0.0138795813
274 0.0053483991 0.0053483991 0.0053483991 0.0053483991
275 0.0143158624 0.0143158624 0.0143158624 0.0143158624
276 0.0062331805 0.0062331805 0.0062331805 0.0062331805
277 -0.0381076441 -0.0381076441 -0.0381076441 -0.0381076441
278 -0.1156345445 -0.1156345445 -0.1156345445 -0.1156345445
279 -0.0839690399 -0.0839690399 -0.0839690399 -0.0839690399
280 -0.0201802758 -0.0201802758 -0.0201802758 -0.0201802758
281 0.0286065568 0.0286065568 0.0286065568 0.0286065568
282 0.0604689709 0.0604689709 0.0604689709 0.0604689709
283 0.0663822973 0.0663822973 0.0663822973 0.0663822973
284 0.0366058158 0.0366058158 0.0366058158 0.0366058158
285 0.0134722674 0.0134722674 0.0134722674 0.0134722674
286 0.0043916557 0.0043916557 0.0043916557 0.0043916557
287 0.0155103422 0.0155103422 0.0155103422 0.0155103422
288 0.0068456549 0.0068456549 0.0068456549 0.0068456549
289 -0.0356416980 -0.0356416980 -0.0356416980 -0.0356416980
290 -0.1186948625 -0.1186948625 -0.1186948625 -0.1186948625
291 -0.0839145855 -0.0839145855 -0.0839145855 -0.0839145855
292 -0.0201078993 -0.0201078993 -0.0201078993 -0.0201078993
293 0.0291431734 0.0291431734 0.0291431734 0.0291431734
294 0.0603561417 0.0603561417 0.0603561417 0.0603561417
295 0.0661343534 0.0661343534 0.0661343534 0.0661343534
296 0.0367875597 0.0367875597 0.0367875597 0.0367875597
297 0.0130640560 0.0130640560 0.0130640560 0.0130640560
298 0.0034683558 0.0034683558 0.0034683558 0.0034683558
299 0.0167275567 0.0167275567 0.0167275567 0.0167275567
300 0.0074538087 0.0074538087 0.0074538087 0.0074538087
301 -0.0332346345 -0.0332346345 -0.0332346345 -0.0332346345
302 -0.1094975179 -0.1094975179 -0.1094975179 -0.1094975179
303 -0.0839114120 -0.0839114120 -0.0839114120 -0.0839114120
304 -0.0202721392 -0.0202721392 -0.0202721392 -0.0202721392
305 0.0275172532 0.0275172532 0.0275172532 0.0275172532
306 0.0606205145 0.0606205145 0.0606205145 0.0606205145
307 0.0668280996 0.0668280996 0.0668280996 0.0668280996
308 0.0362205138 0.0362205138 0.0362205138 0.0362205138
309 0.0142850189 0.0142850189 0.0142850189 0.0142850189
310 0.0063376405 0.0063376405 0.0063376405 0.0063376405
311 0.0131455845 0.0131455845 0.0131455845 0.0131455845
312 0.0056177785 0.0056177785 0.0056177785 0.0056177785
313 -0.0406308126 -0.0406308126 -0.0406308126 -0.0406308126
314 -0.1125675613 -0.1125675613 -0.1125675613 -0.1125675613
315 -0.0839678813 -0.0839678813 -0.0839678813 -0.0839678813
316 -0.0202353637 -0.0202353637 -0.0202353637 -0.0202353637
317 0.0280641464 0.0280641464 0.0280641464 0.0280641464
318 0.0605569983 0.0605569983 0.0605569983 0.0605569983
319 0.0666136819 0.0666136819 0.0666136819 0.0666136819
320 0.0364169327 0.0364169327 0.0364169327 0.0364169327
321 0.0138795813 0.0138795813 0.0138795813 0.0138795813
322 0.0053483991 0.0053483991 0.0053483991 0.0053483991
323 0.0143158624 0.0143158624 0.0143158624 0.0143158624
324 0.0097938977 0.0097938977 0.0097938977 0.0097938977
325 0.0057438420 0.0057438420 0.0057438420 0.0057438420
326 0.0022368374 0.0022368374 0.0022368374 0.0022368374
327 -0.0006722205 -0.0006722205 -0.0006722205 -0.0006722205
328 -0.0029459602 -0.0029459602 -0.0029459602 -0.0029459602
329 -0.0045653078 -0.0045653078 -0.0045653078 -0.0045653078
330 -0.0055297348 -0.0055297348 -0.0055297348 -0.0055297348
331 -0.0058569734 -0.0058569734 -0.0058569734 -0.0058569734
332 -0.0055822085 -0.0055822085 -0.0055822085 -0.0055822085
333 -0.0047567706 -0.0047567706 -0.0047567706 -0.0047567706
334 -0.0034463678 -0.0034463678 -0.0034463678 -0.0034463678
335 -0.0017289095 -0.0017289095 -0.0017289095 -0.0017289095
336 0.0003080125 0.0003080125 0.0003080125 0.0003080125
337 0.0025699130 0.0025699130 0.0025699130 0.0025699130
338 0.0049583870 0.0049583870 0.0049583870 0.0049583870
339 0.0073741811 0.0073741811 0.0073741811 0.0073741811
340 0.0097202697 0.0097202697 0.0097202697 0.0097202697
341 0.0119048436 0.0119048436 0.0119048436 0.0119048436
342 0.0138441212 0.0138441212 0.0138441212 0.0138441212
343 0.0154648967 0.0154648967 0.0154648967 0.0154648967
344 0.0167067475 0.0167067475 0.0167067475 0.0167067475
345 0.0175238316 0.0175238316 0.0175238316 0.0175238316
346 0.0178862212 0.0178862212 0.0178862212 0.0178862212
347 0.0177807266 0.0177807266 0.0177807266 0.0177807266
348 0.0172111854 0.0172111854 0.0172111854 0.0172111854
349 0.0161982033 0.0161982033 0.0161982033 0.0161982033
350 0.0147783524 0.0147783524 0.0147783524 0.0147783524
351 0.0130028463 0.0130028463 0.0130028463 0.0130028463
352 0.0109357306 0.0109357306 0.0109357306 0.0109357306
353 0.0086516389 0.0086516389 0.0086516389 0.0086516389
354 0.0062331805 0.0062331805 0.0062331805 0.0062331805
355 0.0037680361 0.0037680361 0.0037680361 0.0037680361
356 0.0013458487 0.0013458487 0.0013458487 0.0013458487
357 -0.0009449970 -0.0009449970 -0.0009449970 -0.0009449970
358 -0.0030206093 -0.0030206093 -0.0030206093 -0.0030206093
359 -0.0048047364 -0.0048047364 -0.0048047364 -0.0048047364
360 -0.0062317303 -0.0062317303 -0.0062317303 -0.0062317303
361 -0.0072492306 -0.0072492306 -0.0072492306 -0.0072492306
362 -0.0078204824 -0.0078204824 -0.0078204824 -0.0078204824
363 -0.0079262115 -0.0079262115 -0.0079262115 -0.0079262115
364 -0.0075659894 -0.0075659894 -0.0075659894 -0.0075659894
365 -0.0067590385 -0.0067590385 -0.0067590385 -0.0067590385
366 -0.0055444409 -0.0055444409 -0.0055444409 -0.0055444409
367 -0.0039807321 -0.0039807321 -0.0039807321 -0.0039807321
368 -0.0021448791 -0.0021448791 -0.0021448791 -0.0021448791
369 -0.0001306592 -0.0001306592 -0.0001306592 -0.0001306592
370 0.0019535261 0.0019535261 0.0019535261 0.0019535261
371 0.0039873491 0.0039873491 0.0039873491 0.0039873491
372 0.0058417007 0.0058417007 0.0058417007 0.0058417007
373 0.0073821993 0.0073821993 0.0073821993 0.0073821993
374 0.0084729711 0.0084729711 0.0084729711 0.0084729711
375 0.0089806008 0.0089806008 0.0089806008 0.0089806008
376 0.0087781417 0.0087781417 0.0087781417 0.0087781417
377 0.0077490755 0.0077490755 0.0077490755 0.0077490755
378 0.0057911067 0.0057911067 0.0057911067 0.0057911067
379 0.0028196833 0.0028196833 0.0028196833 0.0028196833
380 -0.0012288609 -0.0012288609 -0.0012288609 -0.0012288609
381 -0.0063946379 -0.0063946379 -0.0063946379 -0.0063946379
382 -0.0126920941 -0.0126920941 -0.0126920941 -0.0126920941
383 -0.0201085262 -0.0201085262 -0.0201085262 -0.0201085262
384 -0.0286032763 -0.0286032763 -0.0286032763 -0.0286032763
385 -0.0381076441 -0.0381076441 -0.0381076441 -0.0381076441
386 -0.0485255308 -0.0485255308 -0.0485255308 -0.0485255308
387 -0.0597348122 -0.0597348122 -0.0597348122 -0.0597348122
388 -0.0715894189 -0.0715894189 -0.0715894189 -0.0715894189
389 -0.0839220801 -0.0839220801 -0.0839220801 -0.0839220801
390 -0.0965476714 -0.0965476714 -0.0965476714 -0.0965476714
391 -0.1092670889 -0.1092670889 -0.1092670889 -0.1092670889
392 -0.1218715561 -0.1218715561 -0.1218715561 -0.1218715561
393 -0.1341472607 -0.1341472607 -0.1341472607 -0.1341472607
394 -0.1458802029 -0.1458802029 -0.1458802029 -0.1458802029
395 -0.1568611375 -0.1568611375 -0.1568611375 -0.1568611375
396 -0.1668904803 -0.1668904803 -0.1668904803 -0.1668904803
397 -0.1757830560 -0.1757830560 -0.1757830560 -0.1757830560
398 -0.1833725635 -0.1833725635 -0.1833725635 -0.1833725635
399 -0.1895156431 -0.1895156431 -0.1895156431 -0.1895156431
400 -0.1940954375 -0.1940954375 -0.1940954375 -0.1940954375
401 -0.1970245542 -0.1970245542 -0.1970245542 -0.1970245542
402 -0.1982473485 -0.1982473485 -0.1982473485 -0.1982473485
403 -0.1977414655 -0.1977414655 -0.1977414655 -0.1977414655
404 -0.1955185976 -0.1955185976 -0.1955185976 -0.1955185976
405 -0.1916244351 -0.1916244351 -0.1916244351 -0.1916244351
406 -0.1861378059 -0.1861378059 -0.1861378059 -0.1861378059
407 -0.1791690250 -0.1791690250 -0.1791690250 -0.1791690250
408 -0.1708574906 -0.1708574906 -0.1708574906 -0.1708574906
409 -0.1613685865 -0.1613685865 -0.1613685865 -0.1613685865
410 -0.1508899674 -0.1508899674 -0.1508899674 -0.1508899674
411 -0.1396273173 -0.1396273173 -0.1396273173 -0.1396273173
412 -0.1277996900 -0.1277996900 -0.1277996900 -0.1277996900
413 -0.1156345445 -0.1156345445 -0.1156345445 -0.1156345445
414 -0.1033626029 -0.1033626029 -0.1033626029 -0.1033626029
415 -0.0912126558 -0.0912126558 -0.0912126558 -0.0912126558
416 -0.0794064475 -0.0794064475 -0.0794064475 -0.0794064475
417 -0.0681537660 -0.0681537660 -0.0681537660 -0.0681537660
418 -0.0576478593 -0.0576478593 -0.0576478593 -0.0576478593
419 -0.0480612910 -0.0480612910 -0.0480612910 -0.0480612910
420 -0.0395423341 -0.0395423341 -0.0395423341 -0.0395423341
421 -0.0322119896 -0.0322119896 -0.0322119896 -0.0322119896
422 -0.0261616990 -0.0261616990 -0.0261616990 -0.0261616990
423 -0.0214518011 -0.0214518011 -0.0214518011 -0.0214518011
424 -0.0181107641 -0.0181107641 -0.0181107641 -0.0181107641
425 -0.0161352044 -0.0161352044 -0.0161352044 -0.0161352044
426 -0.0154906818 -0.0154906818 -0.0154906818 -0.0154906818
427 -0.0161132408 -0.0161132408 -0.0161132408 -0.0161132408
428 -0.0179116504 -0.0179116504 -0.0179116504 -0.0179116504
429 -0.0207702755 -0.0207702755 -0.0207702755 -0.0207702755
430 -0.0245524960 -0.0245524960 -0.0245524960 -0.0245524960
431 -0.0291045799 -0.0291045799 -0.0291045799 -0.0291045799
432 -0.0342599038 -0.0342599038 -0.0342599038 -0.0342599038
433 -0.0398434042 -0.0398434042 -0.0398434042 -0.0398434042
434 -0.0456761445 -0.0456761445 -0.0456761445 -0.0456761445
435 -0.0515798738 -0.0515798738 -0.0515798738 -0.0515798738
436 -0.0573814622 -0.0573814622 -0.0573814622 -0.0573814622
437 -0.0629170960 -0.0629170960 -0.0629170960 -0.0629170960
438 -0.0680361313 -0.0680361313 -0.0680361313 -0.0680361313
439 -0.0726045070 -0.0726045070 -0.0726045070 -0.0726045070
440 -0.0765076399 -0.0765076399 -0.0765076399 -0.0765076399
441 -0.0796527327 -0.0796527327 -0.0796527327 -0.0796527327
442 -0.0819704471 -0.0819704471 -0.0819704471 -0.0819704471
443 -0.0834159098 -0.0834159098 -0.0834159098 -0.0834159098
444 -0.0839690399 -0.0839690399 -0.0839690399 -0.0839690399
445 -0.0836342014 -0.0836342014 -0.0836342014 -0.0836342014
446 -0.0824392078 -0.0824392078 -0.0824392078 -0.0824392078
447 -0.0804337169 -0.0804337169 -0.0804337169 -0.0804337169
448 -0.0776870769 -0.0776870769 -0.0776870769 -0.0776870769
449 -0.0742856923 -0.0742856923 -0.0742856923 -0.0742856923
450 -0.0703299948 -0.0703299948 -0.0703299948 -0.0703299948
451 -0.0659311117 -0.0659311117 -0.0659311117 -0.0659311117
452 -0.0612073312 -0.0612073312 -0.0612073312 -0.0612073312
453 -0.0562804689 -0.0562804689 -0.0562804689 -0.0562804689
454 -0.0512722385 -0.0512722385 -0.0512722385 -0.0512722385
455 -0.0463007305 -0.0463007305 -0.0463007305 -0.0463007305
456 -0.0414770952 -0.0414770952 -0.0414770952 -0.0414770952
457 -0.0369025199 -0.0369025199 -0.0369025199 -0.0369025199
458 -0.0326655812 -0.0326655812 -0.0326655812 -0.0326655812
459 -0.0288400379 -0.0288400379 -0.0288400379 -0.0288400379
460 -0.0254831205 -0.0254831205 -0.0254831205 -0.0254831205
461 -0.0226343543 -0.0226343543 -0.0226343543 -0.0226343543
462 -0.0203149398 -0.0203149398 -0.0203149398 -0.0203149398
463 -0.0185276957 -0.0185276957 -0.0185276957 -0.0185276957
464 -0.0172575540 -0.0172575540 -0.0172575540 -0.0172575540
465 -0.0164725828 -0.0164725828 -0.0164725828 -0.0164725828
466 -0.0161254935 -0.0161254935 -0.0161254935 -0.0161254935
467 -0.0161555800 -0.0161555800 -0.0161555800 -0.0161555800
468 -0.0164910223 -0.0164910223 -0.0164910223 -0.0164910223
469 -0.0170514801 -0.0170514801 -0.0170514801 -0.0170514801
470 -0.0177508932 -0.0177508932 -0.0177508932 -0.0177508932
471 -0.0185004003 -0.0185004003 -0.0185004003 -0.0185004003
472 -0.0192112879 -0.0192112879 -0.0192112879 -0.0192112879
473 -0.0197978789 -0.0197978789 -0.0197978789 -0.0197978789
474 -0.0201802758 -0.0201802758 -0.0201802758 -0.0201802758
475 -0.0202868780 -0.0202868780 -0.0202868780 -0.0202868780
476 -0.0200565996 -0.0200565996 -0.0200565996 -0.0200565996
477 -0.0194407278 -0.0194407278 -0.0194407278 -0.0194407278
478 -0.0184043675 -0.0184043675 -0.0184043675 -0.0184043675
479 -0.0169274378 -0.0169274378 -0.0169274378 -0.0169274378
480 -0.0150051934 -0.0150051934 -0.0150051934 -0.0150051934
481 -0.0126482637 -0.0126482637 -0.0126482637 -0.0126482637
482 -0.0098822133 -0.0098822133 -0.0098822133 -0.0098822133
483 -0.0067466436 -0.0067466436 -0.0067466436 -0.0067466436
484 -0.0032938685 -0.0032938685 -0.0032938685 -0.0032938685
485 0.0004127907 0.0004127907 0.0004127907 0.0004127907
486 0.0043010353 0.0043010353 0.0043010353 0.0043010353
487 0.0082918795 0.0082918795 0.0082918795 0.0082918795
488 0.0123021272 0.0123021272 0.0123021272 0.0123021272
489 0.0162469609 0.0162469609 0.0162469609 0.0162469609
490 0.0200425603 0.0200425603 0.0200425603 0.0200425603
491 0.0236086740 0.0236086740 0.0236086740 0.0236086740
492 0.0268710650 0.0268710650 0.0268710650 0.0268710650
493 0.0297637579 0.0297637579 0.0297637579 0.0297637579
494 0.0322310229 0.0322310229 0.0322310229 0.0322310229
495 0.0342290372 0.0342290372 0.0342290372 0.0342290372
496 0.0357271781 0.0357271781 0.0357271781 0.0357271781
497 0.0367089122 0.0367089122 0.0367089122 0.0367089122
498 0.0371722560 0.0371722560 0.0371722560 0.0371722560
499 0.0371297990 0.0371297990 0.0371297990 0.0371297990
500 0.0366082921 0.0366082921 0.0366082921 0.0366082921
501 0.0356478162 0.0356478162 0.0356478162 0.0356478162
502 0.0343005606 0.0343005606 0.0343005606 0.0343005606
503 0.0326292505 0.0326292505 0.0326292505 0.0326292505
504 0.0307052723 0.0307052723 0.0307052723 0.0307052723
505 0.0286065568 0.0286065568 0.0286065568 0.0286065568
506 0.0264152844 0.0264152844 0.0264152844 0.0264152844
507 0.0242154818 0.0242154818 0.0242154818 0.0242154818
508 0.0220905831 0.0220905831 0.0220905831 0.0220905831
509 0.0201210281 0.0201210281 0.0201210281 0.0201210281
510 0.0183819674 0.0183819674 0.0183819674 0.0183819674
511 0.0169411437 0.0169411437 0.0169411437 0.0169411437
512 0.0158570079 0.0158570079 0.0158570079 0.0158570079
513 0.0151771255 0.0151771255 0.0151771255 0.0151771255
514 0.0149369168 0.0149369168 0.0149369168 0.0149369168
515 0.0151587651 0.0151587651 0.0151587651 0.0151587651
516 0.0158515160 0.0158515160 0.0158515160 0.0158515160
517 0.0170103778 0.0170103778 0.0170103778 0.0170103778
518 0.0186172227 0.0186172227 0.0186172227 0.0186172227
519 0.0206412753 0.0206412753 0.0206412753 0.0206412753
520 0.0230401640 0.0230401640 0.0230401640 0.0230401640
521 0.0257612991 0.0257612991 0.0257612991 0.0257612991
522 0.0287435353 0.0287435353 0.0287435353 0.0287435353
523 0.0319190636 0.0319190636 0.0319190636 0.0319190636
524 0.0352154759 0.0352154759 0.0352154759 0.0352154759
525 0.0385579367 0.0385579367 0.0385579367 0.0385579367
526 0.0418713986 0.0418713986 0.0418713986 0.0418713986
527 0.0450827930 0.0450827930 0.0450827930 0.0450827930
528 0.0481231319 0.0481231319 0.0481231319 0.0481231319
529 0.0509294598 0.0509294598 0.0509294598 0.0509294598
530 0.0534465976 0.0534465976 0.0534465976 0.0534465976
531 0.0556286309 0.0556286309 0.0556286309 0.0556286309
532 0.0574401005 0.0574401005 0.0574401005 0.0574401005
533 0.0588568630 0.0588568630 0.0588568630 0.0588568630
534 0.0598666009 0.0598666009 0.0598666009 0.0598666009
535 0.0604689709 0.0604689709 0.0604689709 0.0604689709
536 0.0606753904 0.0606753904 0.0606753904 0.0606753904
537 0.0605084749 0.0605084749 0.0605084749 0.0605084749
538 0.0600011464 0.0600011464 0.0600011464 0.0600011464
539 0.0591954451 0.0591954451 0.0591954451 0.0591954451
540 0.0581410846 0.0581410846 0.0581410846 0.0581410846
541 0.0568937970 0.0568937970 0.0568937970 0.0568937970
542 0.0555135223 0.0555135223 0.0555135223 0.0555135223
543 0.0540624982 0.0540624982 0.0540624982 0.0540624982
544 0.0526033104 0.0526033104 0.0526033104 0.0526033104
545 0.0511969635 0.0511969635 0.0511969635 0.0511969635
546 0.0499010308 0.0499010308 0.0499010308 0.0499010308
547 0.0487679388 0.0487679388 0.0487679388 0.0487679388
548 0.0478434363 0.0478434363 0.0478434363 0.0478434363
549 0.0471652940 0.0471652940 0.0471652940 0.0471652940
550 0.0467622691 0.0467622691 0.0467622691 0.0467622691
551 0.0466533650 0.0466533650 0.0466533650 0.0466533650
552 0.0468474037 0.0468474037 0.0468474037 0.0468474037
553 0.0473429185 0.0473429185 0.0473429185 0.0473429185
554 0.0481283687 0.0481283687 0.0481283687 0.0481283687
555 0.0491826612 0.0491826612 0.0491826612 0.0491826612
556 0.0504759608 0.0504759608 0.0504759608 0.0504759608
557 0.0519707592 0.0519707592 0.0519707592 0.0519707592
558 0.0536231645 0.0536231645 0.0536231645 0.0536231645
559 0.0553843691 0.0553843691 0.0553843691 0.0553843691
560 0.0572022455 0.0572022455 0.0572022455 0.0572022455
561 0.0590230201 0.0590230201 0.0590230201 0.0590230201
562 0.0607929689 0.0607929689 0.0607929689 0.0607929689
563 0.0624600830 0.0624600830 0.0624600830 0.0624600830
564 0.0639756499 0.0639756499 0.0639756499 0.0639756499
565 0.0652957036 0.0652957036 0.0652957036 0.0652957036
566 0.0663822973 0.0663822973 0.0663822973 0.0663822973
567 0.0672045620 0.0672045620 0.0672045620 0.0672045620
568 0.0677395196 0.0677395196 0.0677395196 0.0677395196
569 0.0679726285 0.0679726285 0.0679726285 0.0679726285
570 0.0678980473 0.0678980473 0.0678980473 0.0678980473
571 0.0675186128 0.0675186128 0.0675186128 0.0675186128
572 0.0668455368 0.0668455368 0.0668455368 0.0668455368
573 0.0658978363 0.0658978363 0.0658978363 0.0658978363
574 0.0647015175 0.0647015175 0.0647015175 0.0647015175
575 0.0632885473 0.0632885473 0.0632885473 0.0632885473
576 0.0616956450 0.0616956450 0.0616956450 0.0616956450
577 0.0599629401 0.0599629401 0.0599629401 0.0599629401
578 0.0581325402 0.0581325402 0.0581325402 0.0581325402
579 0.0562470599 0.0562470599 0.0562470599 0.0562470599
580 0.0543481583 0.0543481583 0.0543481583 0.0543481583
581 0.0524751365 0.0524751365 0.0524751365 0.0524751365
582 0.0506636402 0.0506636402 0.0506636402 0.0506636402
583 0.0489445117 0.0489445117 0.0489445117 0.0489445117
584 0.0473428278 0.0473428278 0.0473428278 0.0473428278
585 0.0458771561 0.0458771561 0.0458771561 0.0458771561
586 0.0445590527 0.0445590527 0.0445590527 0.0445590527
587 0.0433928173 0.0433928173 0.0433928173 0.0433928173
588 0.0423755127 0.0423755127 0.0423755127 0.0423755127
589 0.0414972461 0.0414972461 0.0414972461 0.0414972461
590 0.0407417027 0.0407417027 0.0407417027 0.0407417027
591 0.0400869097 0.0400869097 0.0400869097 0.0400869097
592 0.0395062070 0.0395062070 0.0395062070 0.0395062070
593 0.0389693869 0.0389693869 0.0389693869 0.0389693869
594 0.0384439650 0.0384439650 0.0384439650 0.0384439650
595 0.0378965377 0.0378965377 0.0378965377 0.0378965377
596 0.0372941769 0.0372941769 0.0372941769 0.0372941769
597 0.0366058158 0.0366058158 0.0366058158 0.0366058158
598 0.0358035740 0.0358035740 0.0358035740 0.0358035740
599 0.0348639767 0.0348639767 0.0348639767 0.0348639767
600 0.0337690237 0.0337690237 0.0337690237 0.0337690237
601 0.0325070686 0.0325070686 0.0325070686 0.0325070686
602 0.0310734767 0.0310734767 0.0310734767 0.0310734767
603 0.0294710346 0.0294710346 0.0294710346 0.0294710346
604 0.0277100955 0.0277100955 0.0277100955 0.0277100955
605 0.0258084501 0.0258084501 0.0258084501 0.0258084501
606 0.0237909251 0.0237909251 0.0237909251 0.0237909251
607 0.0216887184 0.0216887184 0.0216887184 0.0216887184
608 0.0195384899 0.0195384899 0.0195384899 0.0195384899
609 0.0173812348 0.0173812348 0.0173812348 0.0173812348
610 0.0152609753 0.0152609753 0.0152609753 0.0152609753
611 0.0132233114 0.0132233114 0.0132233114 0.0132233114
612 0.0113138773 0.0113138773 0.0113138773 0.0113138773
613 0.0095767557 0.0095767557 0.0095767557 0.0095767557
614 0.0080529006 0.0080529006 0.0080529006 0.0080529006
615 0.0067786248 0.0067786248 0.0067786248 0.0067786248
616 0.0057842010 0.0057842010 0.0057842010 0.0057842010
617 0.0050926296 0.0050926296 0.0050926296 0.0050926296
618 0.0047186151 0.0047186151 0.0047186151 0.0047186151
619 0.0046677912 0.0046677912 0.0046677912 0.0046677912
620 0.0049362258 0.0049362258 0.0049362258 0.0049362258
621 0.0055102291 0.0055102291 0.0055102291 0.0055102291
622 0.0063664776 0.0063664776 0.0063664776 0.0063664776
623 0.0074724579 0.0074724579 0.0074724579 0.0074724579
624 0.0087872241 0.0087872241 0.0087872241 0.0087872241
625 0.0102624514 0.0102624514 0.0102624514 0.0102624514
626 0.0118437590 0.0118437590 0.0118437590 0.0118437590
627 0.0134722674 0.0134722674 0.0134722674 0.0134722674
628 0.0150863459 0.0150863459 0.0150863459 0.0150863459
629 0.0166234984 0.0166234984 0.0166234984 0.0166234984
630 0.0180223329 0.0180223329 0.0180223329 0.0180223329
631 0.0192245539 0.0192245539 0.0192245539 0.0192245539
632 0.0201769146 0.0201769146 0.0201769146 0.0201769146
633 0.0208330695 0.0208330695 0.0208330695 0.0208330695
634 0.0211552645 0.0211552645 0.0211552645 0.0211552645
635 0.0211158093 0.0211158093 0.0211158093 0.0211158093
636 0.0206982818 0.0206982818 0.0206982818 0.0206982818
637 0.0198984196 0.0198984196 0.0198984196 0.0198984196
638 0.0187246640 0.0187246640 0.0187246640 0.0187246640
639 0.0171983323 0.0171983323 0.0171983323 0.0171983323
640 0.0153534026 0.0153534026 0.0153534026 0.0153534026
641 0.0132359096 0.0132359096 0.0132359096 0.0132359096
642 0.0109029597 0.0109029597 0.0109029597 0.0109029597
643 0.0084213862 0.0084213862 0.0084213862 0.0084213862
644 0.0058660759 0.0058660759 0.0058660759 0.0058660759
645 0.0033180099 0.0033180099 0.0033180099 0.0033180099
646 0.0008620702 0.0008620702 0.0008620702 0.0008620702
647 -0.0014153287 -0.0014153287 -0.0014153287 -0.0014153287
648 -0.0034287175 -0.0034287175 -0.0034287175 -0.0034287175
649 -0.0050960878 -0.0050960878 -0.0050960878 -0.0050960878
650 -0.0063413743 -0.0063413743 -0.0063413743 -0.0063413743
651 -0.0070968298 -0.0070968298 -0.0070968298 -0.0070968298
652 -0.0073052214 -0.0073052214 -0.0073052214 -0.0073052214
653 -0.0069217820 -0.0069217820 -0.0069217820 -0.0069217820
654 -0.0059158544 -0.0059158544 -0.0059158544 -0.0059158544
655 -0.0042721757 -0.0042721757 -0.0042721757 -0.0042721757
656 -0.0019917584 -0.0019917584 -0.0019917584 -0.0019917584
657 0.0009076652 0.0009076652 0.0009076652 0.0009076652
658 0.0043916557 0.0043916557 0.0043916557 0.0043916557
659 0.0084095428 0.0084095428 0.0084095428 0.0084095428
660 0.0128953614 0.0128953614 0.0128953614 0.0128953614
661 0.0177692278 0.0177692278 0.0177692278 0.0177692278
662 0.0229391233 0.0229391233 0.0229391233 0.0229391233
663 0.0283030431 0.0283030431 0.0283030431 0.0283030431
664 0.0337514543 0.0337514543 0.0337514543 0.0337514543
665 0.0391699992 0.0391699992 0.0391699992 0.0391699992
666 0.0444423708 0.0444423708 0.0444423708 0.0444423708
667 0.0494532841 0.0494532841 0.0494532841 0.0494532841
668 0.0540914595 0.0540914595 0.0540914595 0.0540914595
669 0.0582525370 0.0582525370 0.0582525370 0.0582525370
670 0.0618418386 0.0618418386 0.0618418386 0.0618418386
671 0.0647769010 0.0647769010 0.0647769010 0.0647769010
672 0.0669897051 0.0669897051 0.0669897051 0.0669897051
673 0.0684285394 0.0684285394 0.0684285394 0.0684285394
674 0.0690594396 0.0690594396 0.0690594396 0.0690594396
675 0.0688671642 0.0688671642 0.0688671642 0.0688671642
676 0.0678556731 0.0678556731 0.0678556731 0.0678556731
677 0.0660480935 0.0660480935 0.0660480935 0.0660480935
678 0.0634861709 0.0634861709 0.0634861709 0.0634861709
679 0.0602292165 0.0602292165 0.0602292165 0.0602292165
680 0.0563525797 0.0563525797 0.0563525797 0.0563525797
681 0.0519456827 0.0519456827 0.0519456827 0.0519456827
682 0.0471096734 0.0471096734 0.0471096734 0.0471096734
683 0.0419547590 0.0419547590 0.0419547590 0.0419547590
684 0.0365972934 0.0365972934 0.0365972934 0.0365972934
685 0.0311567007 0.0311567007 0.0311567007 0.0311567007
686 0.0257523196 0.0257523196 0.0257523196 0.0257523196
687 0.0205002574 0.0205002574 0.0205002574 0.0205002574
688 0.0155103422 0.0155103422 0.0155103422 0.0155103422
multiplicative_terms multiplicative_terms_lower multiplicative_terms_upper
1 0 0 0
2 0 0 0
3 0 0 0
4 0 0 0
5 0 0 0
6 0 0 0
7 0 0 0
8 0 0 0
9 0 0 0
10 0 0 0
11 0 0 0
12 0 0 0
13 0 0 0
14 0 0 0
15 0 0 0
16 0 0 0
17 0 0 0
18 0 0 0
19 0 0 0
20 0 0 0
21 0 0 0
22 0 0 0
23 0 0 0
24 0 0 0
25 0 0 0
26 0 0 0
27 0 0 0
28 0 0 0
29 0 0 0
30 0 0 0
31 0 0 0
32 0 0 0
33 0 0 0
34 0 0 0
35 0 0 0
36 0 0 0
37 0 0 0
38 0 0 0
39 0 0 0
40 0 0 0
41 0 0 0
42 0 0 0
43 0 0 0
44 0 0 0
45 0 0 0
46 0 0 0
47 0 0 0
48 0 0 0
49 0 0 0
50 0 0 0
51 0 0 0
52 0 0 0
53 0 0 0
54 0 0 0
55 0 0 0
56 0 0 0
57 0 0 0
58 0 0 0
59 0 0 0
60 0 0 0
61 0 0 0
62 0 0 0
63 0 0 0
64 0 0 0
65 0 0 0
66 0 0 0
67 0 0 0
68 0 0 0
69 0 0 0
70 0 0 0
71 0 0 0
72 0 0 0
73 0 0 0
74 0 0 0
75 0 0 0
76 0 0 0
77 0 0 0
78 0 0 0
79 0 0 0
80 0 0 0
81 0 0 0
82 0 0 0
83 0 0 0
84 0 0 0
85 0 0 0
86 0 0 0
87 0 0 0
88 0 0 0
89 0 0 0
90 0 0 0
91 0 0 0
92 0 0 0
93 0 0 0
94 0 0 0
95 0 0 0
96 0 0 0
97 0 0 0
98 0 0 0
99 0 0 0
100 0 0 0
101 0 0 0
102 0 0 0
103 0 0 0
104 0 0 0
105 0 0 0
106 0 0 0
107 0 0 0
108 0 0 0
109 0 0 0
110 0 0 0
111 0 0 0
112 0 0 0
113 0 0 0
114 0 0 0
115 0 0 0
116 0 0 0
117 0 0 0
118 0 0 0
119 0 0 0
120 0 0 0
121 0 0 0
122 0 0 0
123 0 0 0
124 0 0 0
125 0 0 0
126 0 0 0
127 0 0 0
128 0 0 0
129 0 0 0
130 0 0 0
131 0 0 0
132 0 0 0
133 0 0 0
134 0 0 0
135 0 0 0
136 0 0 0
137 0 0 0
138 0 0 0
139 0 0 0
140 0 0 0
141 0 0 0
142 0 0 0
143 0 0 0
144 0 0 0
145 0 0 0
146 0 0 0
147 0 0 0
148 0 0 0
149 0 0 0
150 0 0 0
151 0 0 0
152 0 0 0
153 0 0 0
154 0 0 0
155 0 0 0
156 0 0 0
157 0 0 0
158 0 0 0
159 0 0 0
160 0 0 0
161 0 0 0
162 0 0 0
163 0 0 0
164 0 0 0
165 0 0 0
166 0 0 0
167 0 0 0
168 0 0 0
169 0 0 0
170 0 0 0
171 0 0 0
172 0 0 0
173 0 0 0
174 0 0 0
175 0 0 0
176 0 0 0
177 0 0 0
178 0 0 0
179 0 0 0
180 0 0 0
181 0 0 0
182 0 0 0
183 0 0 0
184 0 0 0
185 0 0 0
186 0 0 0
187 0 0 0
188 0 0 0
189 0 0 0
190 0 0 0
191 0 0 0
192 0 0 0
193 0 0 0
194 0 0 0
195 0 0 0
196 0 0 0
197 0 0 0
198 0 0 0
199 0 0 0
200 0 0 0
201 0 0 0
202 0 0 0
203 0 0 0
204 0 0 0
205 0 0 0
206 0 0 0
207 0 0 0
208 0 0 0
209 0 0 0
210 0 0 0
211 0 0 0
212 0 0 0
213 0 0 0
214 0 0 0
215 0 0 0
216 0 0 0
217 0 0 0
218 0 0 0
219 0 0 0
220 0 0 0
221 0 0 0
222 0 0 0
223 0 0 0
224 0 0 0
225 0 0 0
226 0 0 0
227 0 0 0
228 0 0 0
229 0 0 0
230 0 0 0
231 0 0 0
232 0 0 0
233 0 0 0
234 0 0 0
235 0 0 0
236 0 0 0
237 0 0 0
238 0 0 0
239 0 0 0
240 0 0 0
241 0 0 0
242 0 0 0
243 0 0 0
244 0 0 0
245 0 0 0
246 0 0 0
247 0 0 0
248 0 0 0
249 0 0 0
250 0 0 0
251 0 0 0
252 0 0 0
253 0 0 0
254 0 0 0
255 0 0 0
256 0 0 0
257 0 0 0
258 0 0 0
259 0 0 0
260 0 0 0
261 0 0 0
262 0 0 0
263 0 0 0
264 0 0 0
265 0 0 0
266 0 0 0
267 0 0 0
268 0 0 0
269 0 0 0
270 0 0 0
271 0 0 0
272 0 0 0
273 0 0 0
274 0 0 0
275 0 0 0
276 0 0 0
277 0 0 0
278 0 0 0
279 0 0 0
280 0 0 0
281 0 0 0
282 0 0 0
283 0 0 0
284 0 0 0
285 0 0 0
286 0 0 0
287 0 0 0
288 0 0 0
289 0 0 0
290 0 0 0
291 0 0 0
292 0 0 0
293 0 0 0
294 0 0 0
295 0 0 0
296 0 0 0
297 0 0 0
298 0 0 0
299 0 0 0
300 0 0 0
301 0 0 0
302 0 0 0
303 0 0 0
304 0 0 0
305 0 0 0
306 0 0 0
307 0 0 0
308 0 0 0
309 0 0 0
310 0 0 0
311 0 0 0
312 0 0 0
313 0 0 0
314 0 0 0
315 0 0 0
316 0 0 0
317 0 0 0
318 0 0 0
319 0 0 0
320 0 0 0
321 0 0 0
322 0 0 0
323 0 0 0
324 0 0 0
325 0 0 0
326 0 0 0
327 0 0 0
328 0 0 0
329 0 0 0
330 0 0 0
331 0 0 0
332 0 0 0
333 0 0 0
334 0 0 0
335 0 0 0
336 0 0 0
337 0 0 0
338 0 0 0
339 0 0 0
340 0 0 0
341 0 0 0
342 0 0 0
343 0 0 0
344 0 0 0
345 0 0 0
346 0 0 0
347 0 0 0
348 0 0 0
349 0 0 0
350 0 0 0
351 0 0 0
352 0 0 0
353 0 0 0
354 0 0 0
355 0 0 0
356 0 0 0
357 0 0 0
358 0 0 0
359 0 0 0
360 0 0 0
361 0 0 0
362 0 0 0
363 0 0 0
364 0 0 0
365 0 0 0
366 0 0 0
367 0 0 0
368 0 0 0
369 0 0 0
370 0 0 0
371 0 0 0
372 0 0 0
373 0 0 0
374 0 0 0
375 0 0 0
376 0 0 0
377 0 0 0
378 0 0 0
379 0 0 0
380 0 0 0
381 0 0 0
382 0 0 0
383 0 0 0
384 0 0 0
385 0 0 0
386 0 0 0
387 0 0 0
388 0 0 0
389 0 0 0
390 0 0 0
391 0 0 0
392 0 0 0
393 0 0 0
394 0 0 0
395 0 0 0
396 0 0 0
397 0 0 0
398 0 0 0
399 0 0 0
400 0 0 0
401 0 0 0
402 0 0 0
403 0 0 0
404 0 0 0
405 0 0 0
406 0 0 0
407 0 0 0
408 0 0 0
409 0 0 0
410 0 0 0
411 0 0 0
412 0 0 0
413 0 0 0
414 0 0 0
415 0 0 0
416 0 0 0
417 0 0 0
418 0 0 0
419 0 0 0
420 0 0 0
421 0 0 0
422 0 0 0
423 0 0 0
424 0 0 0
425 0 0 0
426 0 0 0
427 0 0 0
428 0 0 0
429 0 0 0
430 0 0 0
431 0 0 0
432 0 0 0
433 0 0 0
434 0 0 0
435 0 0 0
436 0 0 0
437 0 0 0
438 0 0 0
439 0 0 0
440 0 0 0
441 0 0 0
442 0 0 0
443 0 0 0
444 0 0 0
445 0 0 0
446 0 0 0
447 0 0 0
448 0 0 0
449 0 0 0
450 0 0 0
451 0 0 0
452 0 0 0
453 0 0 0
454 0 0 0
455 0 0 0
456 0 0 0
457 0 0 0
458 0 0 0
459 0 0 0
460 0 0 0
461 0 0 0
462 0 0 0
463 0 0 0
464 0 0 0
465 0 0 0
466 0 0 0
467 0 0 0
468 0 0 0
469 0 0 0
470 0 0 0
471 0 0 0
472 0 0 0
473 0 0 0
474 0 0 0
475 0 0 0
476 0 0 0
477 0 0 0
478 0 0 0
479 0 0 0
480 0 0 0
481 0 0 0
482 0 0 0
483 0 0 0
484 0 0 0
485 0 0 0
486 0 0 0
487 0 0 0
488 0 0 0
489 0 0 0
490 0 0 0
491 0 0 0
492 0 0 0
493 0 0 0
494 0 0 0
495 0 0 0
496 0 0 0
497 0 0 0
498 0 0 0
499 0 0 0
500 0 0 0
501 0 0 0
502 0 0 0
503 0 0 0
504 0 0 0
505 0 0 0
506 0 0 0
507 0 0 0
508 0 0 0
509 0 0 0
510 0 0 0
511 0 0 0
512 0 0 0
513 0 0 0
514 0 0 0
515 0 0 0
516 0 0 0
517 0 0 0
518 0 0 0
519 0 0 0
520 0 0 0
521 0 0 0
522 0 0 0
523 0 0 0
524 0 0 0
525 0 0 0
526 0 0 0
527 0 0 0
528 0 0 0
529 0 0 0
530 0 0 0
531 0 0 0
532 0 0 0
533 0 0 0
534 0 0 0
535 0 0 0
536 0 0 0
537 0 0 0
538 0 0 0
539 0 0 0
540 0 0 0
541 0 0 0
542 0 0 0
543 0 0 0
544 0 0 0
545 0 0 0
546 0 0 0
547 0 0 0
548 0 0 0
549 0 0 0
550 0 0 0
551 0 0 0
552 0 0 0
553 0 0 0
554 0 0 0
555 0 0 0
556 0 0 0
557 0 0 0
558 0 0 0
559 0 0 0
560 0 0 0
561 0 0 0
562 0 0 0
563 0 0 0
564 0 0 0
565 0 0 0
566 0 0 0
567 0 0 0
568 0 0 0
569 0 0 0
570 0 0 0
571 0 0 0
572 0 0 0
573 0 0 0
574 0 0 0
575 0 0 0
576 0 0 0
577 0 0 0
578 0 0 0
579 0 0 0
580 0 0 0
581 0 0 0
582 0 0 0
583 0 0 0
584 0 0 0
585 0 0 0
586 0 0 0
587 0 0 0
588 0 0 0
589 0 0 0
590 0 0 0
591 0 0 0
592 0 0 0
593 0 0 0
594 0 0 0
595 0 0 0
596 0 0 0
597 0 0 0
598 0 0 0
599 0 0 0
600 0 0 0
601 0 0 0
602 0 0 0
603 0 0 0
604 0 0 0
605 0 0 0
606 0 0 0
607 0 0 0
608 0 0 0
609 0 0 0
610 0 0 0
611 0 0 0
612 0 0 0
613 0 0 0
614 0 0 0
615 0 0 0
616 0 0 0
617 0 0 0
618 0 0 0
619 0 0 0
620 0 0 0
621 0 0 0
622 0 0 0
623 0 0 0
624 0 0 0
625 0 0 0
626 0 0 0
627 0 0 0
628 0 0 0
629 0 0 0
630 0 0 0
631 0 0 0
632 0 0 0
633 0 0 0
634 0 0 0
635 0 0 0
636 0 0 0
637 0 0 0
638 0 0 0
639 0 0 0
640 0 0 0
641 0 0 0
642 0 0 0
643 0 0 0
644 0 0 0
645 0 0 0
646 0 0 0
647 0 0 0
648 0 0 0
649 0 0 0
650 0 0 0
651 0 0 0
652 0 0 0
653 0 0 0
654 0 0 0
655 0 0 0
656 0 0 0
657 0 0 0
658 0 0 0
659 0 0 0
660 0 0 0
661 0 0 0
662 0 0 0
663 0 0 0
664 0 0 0
665 0 0 0
666 0 0 0
667 0 0 0
668 0 0 0
669 0 0 0
670 0 0 0
671 0 0 0
672 0 0 0
673 0 0 0
674 0 0 0
675 0 0 0
676 0 0 0
677 0 0 0
678 0 0 0
679 0 0 0
680 0 0 0
681 0 0 0
682 0 0 0
683 0 0 0
684 0 0 0
685 0 0 0
686 0 0 0
687 0 0 0
688 0 0 0
yhat_lower yhat_upper trend_lower trend_upper yhat
1 -0.3336425 1.0887446 0.4040040 0.4040040 0.368362317
2 -0.4615623 1.0308333 0.4033586 0.4033586 0.284663711
3 -0.3659768 1.0869277 0.4026440 0.4026440 0.318729393
4 -0.2996758 1.1188668 0.4019524 0.4019524 0.381844535
5 -0.2939512 1.2282141 0.4012378 0.4012378 0.430381013
6 -0.2686735 1.1736492 0.4005463 0.4005463 0.460902437
7 -0.2585181 1.1817130 0.3998317 0.3998317 0.465966053
8 -0.3069143 1.1300960 0.3991171 0.3991171 0.435904664
9 -0.3652590 1.1401033 0.3984256 0.3984256 0.411489617
10 -0.3634121 1.0950413 0.3977110 0.3977110 0.401179321
11 -0.2733108 1.1659633 0.3970194 0.3970194 0.413746978
12 -0.3308393 1.1736920 0.3963048 0.3963048 0.403758635
13 -0.3725682 1.1044370 0.3955902 0.3955902 0.362355596
14 -0.4671592 1.0092589 0.3949217 0.3949217 0.285424220
15 -0.4175071 1.0303796 0.3942071 0.3942071 0.310295731
16 -0.2985540 1.0477548 0.3935156 0.3935156 0.373243460
17 -0.3319745 1.1911636 0.3928010 0.3928010 0.420318257
18 -0.2409697 1.1830807 0.3921095 0.3921095 0.452729974
19 -0.2967192 1.2069732 0.3913949 0.3913949 0.458222964
20 -0.2897116 1.2180719 0.3906803 0.3906803 0.426900783
21 -0.3370635 1.1429707 0.3899887 0.3899887 0.404273744
22 -0.3178430 1.1274494 0.3892741 0.3892741 0.395611770
23 -0.3428913 1.1226217 0.3885826 0.3885826 0.401728170
24 -0.3441793 1.1156865 0.3878680 0.3878680 0.393485769
25 -0.3722057 1.1136395 0.3871534 0.3871534 0.346522582
26 -0.4384275 1.0058620 0.3865080 0.3865080 0.273940393
27 -0.4087352 1.0175066 0.3857934 0.3857934 0.301825477
28 -0.3497773 1.1204603 0.3851018 0.3851018 0.364866451
29 -0.3761403 1.1579151 0.3843872 0.3843872 0.412451366
30 -0.3141200 1.1757939 0.3836957 0.3836957 0.444252674
31 -0.2965745 1.2191521 0.3829811 0.3829811 0.449594762
32 -0.2814869 1.1921537 0.3822665 0.3822665 0.418683417
33 -0.3587158 1.0624432 0.3815749 0.3815749 0.395454522
34 -0.2753765 1.0796206 0.3808603 0.3808603 0.386208744
35 -0.3314254 1.1282238 0.3801688 0.3801688 0.394484664
36 -0.3525201 1.0957839 0.3794542 0.3794542 0.385687386
37 -0.3962980 1.0516480 0.3787396 0.3787396 0.340631967
38 -0.5061410 1.0107646 0.3780942 0.3780942 0.262459625
39 -0.3910370 1.0622793 0.3773796 0.3773796 0.293410534
40 -0.3665822 1.0986493 0.3766880 0.3766880 0.356507755
41 -0.2835991 1.0643637 0.3759734 0.3759734 0.404579992
42 -0.2692347 1.1328277 0.3752819 0.3752819 0.435750862
43 -0.2677526 1.1431072 0.3745673 0.3745673 0.440949593
44 -0.3324945 1.1291569 0.3738527 0.3738527 0.410458516
45 -0.3128360 1.0884774 0.3731612 0.3731612 0.386633424
46 -0.3643841 1.1379880 0.3724466 0.3724466 0.376838217
47 -0.3454521 1.1354516 0.3717550 0.3717550 0.387265359
48 -0.3040366 1.1485341 0.3710404 0.3710404 0.377886076
49 -0.4171331 1.0585164 0.3703258 0.3703258 0.334684128
50 -0.4441894 0.9488890 0.3696804 0.3696804 0.250985523
51 -0.4754200 1.0612195 0.3689658 0.3689658 0.285051204
52 -0.3573673 1.0931985 0.3682742 0.3682742 0.348166346
53 -0.3016336 1.1567825 0.3675597 0.3675597 0.396702824
54 -0.3046331 1.1711581 0.3668681 0.3668681 0.427224248
55 -0.2845741 1.1884212 0.3661535 0.3661535 0.432287864
56 -0.3659672 1.1435627 0.3654389 0.3654389 0.402226475
57 -0.3002709 1.0973784 0.3647474 0.3647474 0.377811427
58 -0.3563939 1.1360337 0.3640328 0.3640328 0.367501132
59 -0.3668311 1.1282404 0.3633412 0.3633412 0.380068789
60 -0.4002033 1.1416803 0.3626266 0.3626266 0.370080445
61 -0.4138915 1.0668625 0.3619120 0.3619120 0.328677406
62 -0.5345292 0.9521599 0.3612435 0.3612435 0.251746030
63 -0.4481509 1.0295441 0.3605290 0.3605290 0.276617541
64 -0.3984690 1.0284107 0.3598374 0.3598374 0.339565270
65 -0.3772800 1.1414122 0.3591228 0.3591228 0.386640067
66 -0.3491312 1.1629631 0.3584313 0.3584313 0.419051784
67 -0.3330643 1.1684597 0.3577167 0.3577167 0.424544773
68 -0.3040714 1.1167170 0.3570021 0.3570021 0.393222592
69 -0.3891934 1.1184365 0.3563105 0.3563105 0.370595553
70 -0.3446236 1.0524771 0.3555959 0.3555959 0.361933579
71 -0.3546046 1.0865772 0.3549044 0.3549044 0.368049979
72 -0.3807498 1.0909830 0.3541898 0.3541898 0.359807578
73 -0.4133118 1.0916205 0.3534752 0.3534752 0.312844391
74 -0.4811643 1.0204277 0.3528298 0.3528298 0.240262201
75 -0.4365740 0.9823234 0.3521152 0.3521152 0.268147286
76 -0.3984152 1.0496820 0.3514236 0.3514236 0.331188259
77 -0.3546002 1.0635831 0.3507090 0.3507090 0.378773174
78 -0.3180881 1.1145949 0.3500175 0.3500175 0.410574482
79 -0.2818528 1.1057745 0.3493029 0.3493029 0.415916570
80 -0.3957460 1.0992685 0.3485883 0.3485883 0.385005225
81 -0.3961885 1.0630921 0.3478967 0.3478967 0.361776330
82 -0.3962105 1.0621297 0.3471822 0.3471822 0.352530552
83 -0.3834038 1.1712012 0.3464906 0.3464906 0.360806471
84 -0.4255525 1.0339176 0.3457760 0.3457760 0.352009194
85 -0.3800891 1.0181523 0.3450614 0.3450614 0.306953774
86 -0.5026952 0.9550300 0.3444160 0.3444160 0.228781432
87 -0.4643012 0.9949985 0.3437014 0.3437014 0.259732342
88 -0.4225584 1.0516275 0.3430098 0.3430098 0.322829562
89 -0.3569951 1.0744448 0.3422952 0.3422952 0.370901799
90 -0.3169004 1.1294774 0.3416037 0.3416037 0.402072669
91 -0.3997236 1.1691740 0.3408891 0.3408891 0.407271400
92 -0.3326847 1.1577786 0.3401745 0.3401745 0.376780323
93 -0.3154802 1.1293402 0.3394830 0.3394830 0.352955230
94 -0.3753331 1.0836967 0.3387684 0.3387684 0.343160023
95 -0.3931812 1.0587095 0.3380768 0.3380768 0.353587165
96 -0.3767172 1.0941296 0.3373622 0.3373622 0.344207883
97 -0.3832198 1.0822448 0.3366476 0.3366476 0.301005934
98 -0.5377112 0.9613758 0.3360022 0.3360022 0.217307329
99 -0.4777252 0.9590609 0.3352876 0.3352876 0.251373010
100 -0.4444453 1.1077354 0.3345961 0.3345961 0.314488152
101 -0.3864553 1.0637906 0.3338815 0.3338815 0.363024629
102 -0.2935299 1.1278051 0.3331899 0.3331899 0.393546054
103 -0.3222467 1.1840150 0.3324753 0.3324753 0.398609670
104 -0.3725357 1.0776990 0.3317607 0.3317607 0.368548280
105 -0.4071125 1.1246856 0.3310692 0.3310692 0.344133233
106 -0.3984752 1.1051496 0.3303546 0.3303546 0.333822937
107 -0.4043440 1.1069790 0.3296630 0.3296630 0.346390594
108 -0.3714432 1.0571191 0.3289484 0.3289484 0.336402250
109 -0.4552772 1.0789367 0.3282338 0.3282338 0.294999211
110 -0.5232312 0.9559235 0.3275654 0.3275654 0.218067835
111 -0.4972787 0.9901056 0.3268508 0.3268508 0.242939346
112 -0.4607488 1.0018501 0.3261592 0.3261592 0.305887075
113 -0.4227021 1.0993980 0.3254446 0.3254446 0.352961872
114 -0.3669849 1.1546838 0.3247531 0.3247531 0.385373589
115 -0.3000268 1.1379415 0.3240384 0.3240384 0.390866542
116 -0.4014610 1.0542492 0.3233238 0.3233238 0.359544324
117 -0.3831286 1.1048820 0.3226322 0.3226322 0.336917250
118 -0.4624125 1.1062162 0.3219176 0.3219176 0.328255240
119 -0.3728840 1.0717294 0.3212260 0.3212260 0.334371604
120 -0.3937192 1.0720995 0.3205114 0.3205114 0.326129166
121 -0.4560283 1.0342396 0.3197968 0.3197968 0.279165943
122 -0.5686753 0.9747545 0.3191513 0.3191513 0.206583721
123 -0.5509285 0.9806867 0.3184367 0.3184367 0.234468769
124 -0.4476125 1.0181873 0.3177451 0.3177451 0.297509707
125 -0.3880553 1.0740819 0.3170300 0.3170300 0.345094140
126 -0.3402375 1.1408353 0.3163380 0.3163380 0.376894982
127 -0.3548794 1.1058127 0.3156229 0.3156229 0.382236588
128 -0.4265809 1.0383040 0.3149078 0.3149078 0.351324762
129 -0.4310188 1.0234619 0.3142158 0.3142158 0.328095401
130 -0.4123944 1.0622141 0.3135007 0.3135007 0.318849141
131 -0.3318329 1.0612495 0.3128087 0.3128087 0.327124595
132 -0.4280086 1.0850784 0.3120937 0.3120937 0.318326836
133 -0.4412634 0.9898486 0.3113786 0.3113786 0.273270934
134 -0.5756933 0.8924985 0.3107327 0.3107327 0.195098157
135 -0.5385549 0.9346847 0.3100176 0.3100176 0.226048585
136 -0.4710397 1.0528071 0.3093252 0.3093252 0.289144962
137 -0.3691528 1.0762786 0.3086098 0.3086098 0.337216328
138 -0.3183827 1.0641701 0.3079174 0.3079174 0.368386355
139 -0.3241880 1.1243485 0.3072019 0.3072019 0.373584215
140 -0.3990803 1.0509717 0.3064865 0.3064865 0.343092267
141 -0.4423636 1.0252210 0.3057941 0.3057941 0.319266332
142 -0.4437709 1.0553844 0.3050786 0.3050786 0.309470254
143 -0.3384232 1.0642780 0.3043862 0.3043862 0.319896553
144 -0.4699179 1.0107079 0.3036707 0.3036707 0.310516399
145 -0.4552288 1.0065949 0.3029553 0.3029553 0.267313580
146 -0.5367642 0.8758196 0.3023030 0.3023030 0.183608161
147 -0.5077798 0.9401266 0.3015809 0.3015809 0.217666300
148 -0.4260281 1.0268224 0.3008820 0.3008820 0.280774142
149 -0.3816066 1.0801866 0.3001599 0.3001599 0.329303076
150 -0.3781573 1.0698971 0.2994611 0.2994611 0.359817201
151 -0.3593157 1.1059916 0.2987389 0.2987389 0.364873274
152 -0.3798318 1.0745448 0.2980168 0.2980168 0.334804342
153 -0.4599481 1.0970061 0.2973179 0.2973179 0.310381995
154 -0.4682950 1.0455552 0.2965958 0.2965958 0.300064156
155 -0.4342961 1.0621877 0.2958970 0.2958970 0.312624514
156 -0.4214767 1.0343005 0.2951661 0.2951661 0.302619904
157 -0.4570204 1.0199859 0.2944352 0.2944352 0.261200600
158 -0.5521846 0.9427051 0.2937515 0.2937515 0.184254008
159 -0.4525314 0.9452093 0.2930207 0.2930207 0.209109252
160 -0.5134189 1.0172984 0.2923134 0.2923134 0.272041240
161 -0.4115877 1.0256363 0.2915825 0.2915825 0.319099771
162 -0.3933378 1.0881201 0.2908752 0.2908752 0.351495747
163 -0.3521641 1.1083584 0.2901444 0.2901444 0.356972471
164 -0.3555581 1.0811762 0.2894135 0.2894135 0.325634024
165 -0.4272193 1.0788606 0.2887062 0.2887062 0.302991244
166 -0.4778102 1.0296410 0.2879708 0.2879708 0.294308398
167 -0.4820453 0.9984801 0.2872590 0.2872590 0.300404598
168 -0.4693800 0.9668939 0.2865235 0.2865235 0.292141324
169 -0.5036697 1.0070951 0.2857881 0.2857881 0.245157265
170 -0.5880443 0.9135872 0.2851238 0.2851238 0.172556222
171 -0.5262476 0.9783249 0.2843883 0.2843883 0.200420434
172 -0.4763964 1.0506994 0.2836766 0.2836766 0.263441208
173 -0.4192971 1.0664115 0.2829411 0.2829411 0.311005250
174 -0.3486641 1.0904313 0.2822294 0.2822294 0.342786359
175 -0.3510678 1.0967880 0.2814939 0.2814939 0.348107574
176 -0.4340835 1.0440962 0.2807584 0.2807584 0.317175357
177 -0.4360758 1.0164617 0.2800416 0.2800416 0.293921190
178 -0.4479829 1.0059547 0.2793009 0.2793009 0.284649298
179 -0.4771566 1.0201551 0.2785841 0.2785841 0.292899946
180 -0.3900649 1.0101409 0.2778434 0.2778434 0.284076555
181 -0.5062108 0.9773526 0.2771027 0.2771027 0.238995021
182 -0.5368176 0.8910808 0.2764336 0.2764336 0.160799093
183 -0.5392430 0.9023504 0.2756929 0.2756929 0.191723888
184 -0.5263381 0.9932578 0.2749761 0.2749761 0.254795837
185 -0.4200024 1.0671557 0.2742354 0.2742354 0.302841960
186 -0.3949195 1.0572869 0.2735186 0.2735186 0.333987558
187 -0.4205355 1.0754690 0.2727619 0.2727619 0.339144186
188 -0.4548584 1.0689818 0.2720052 0.2720052 0.308611005
189 -0.4038611 1.0328356 0.2712729 0.2712729 0.284745168
190 -0.4594152 0.9950532 0.2705162 0.2705162 0.274907857
191 -0.5104226 0.9417432 0.2697839 0.2697839 0.285294254
192 -0.4019297 1.0079581 0.2690272 0.2690272 0.275872867
193 -0.5236384 0.9697370 0.2682705 0.2682705 0.232628816
194 -0.6665124 0.8333953 0.2675870 0.2675870 0.148892181
195 -0.5564518 0.8892780 0.2668303 0.2668303 0.182915759
196 -0.4369524 0.9909812 0.2660981 0.2660981 0.245990156
197 -0.4932227 0.9968851 0.2653114 0.2653114 0.294454568
198 -0.4018827 1.0373175 0.2645501 0.2645501 0.324906252
199 -0.4476050 1.0554555 0.2637634 0.2637634 0.329897803
200 -0.3984648 1.0410141 0.2629768 0.2629768 0.299764348
201 -0.4577182 1.0677183 0.2622155 0.2622155 0.275279560
202 -0.4545908 1.0094183 0.2614288 0.2614288 0.264897199
203 -0.4857741 1.0141674 0.2606676 0.2606676 0.277395116
204 -0.4555136 0.9937212 0.2598809 0.2598809 0.267334707
205 -0.5074849 0.9519974 0.2590942 0.2590942 0.225859603
206 -0.5605718 0.8813138 0.2583583 0.2583583 0.148860812
207 -0.5838614 0.9224444 0.2575717 0.2575717 0.173660257
208 -0.4880133 0.9425277 0.2568059 0.2568059 0.236533724
209 -0.4445076 1.0192855 0.2560145 0.2560145 0.283531783
210 -0.4019942 0.9718116 0.2552487 0.2552487 0.315869238
211 -0.3884654 1.0904928 0.2544574 0.2544574 0.321285490
212 -0.3490466 1.0341233 0.2536661 0.2536661 0.289886571
213 -0.4822779 0.9944498 0.2529003 0.2529003 0.267185270
214 -0.5149370 1.0178165 0.2521089 0.2521089 0.258446558
215 -0.4576114 0.9977912 0.2513431 0.2513431 0.264488696
216 -0.4981577 0.9484744 0.2505518 0.2505518 0.256169557
217 -0.5588444 0.9011569 0.2497604 0.2497604 0.209129632
218 -0.5996060 0.8652346 0.2490421 0.2490421 0.136474560
219 -0.5512689 0.9042366 0.2482468 0.2482468 0.164278952
220 -0.4728812 0.9747995 0.2474772 0.2474772 0.227241837
221 -0.4561988 1.0433719 0.2466819 0.2466819 0.274746059
222 -0.3991009 1.0367696 0.2459123 0.2459123 0.306469278
223 -0.4288538 1.1181482 0.2451170 0.2451170 0.311730674
224 -0.4507312 0.9743359 0.2443217 0.2443217 0.280738638
225 -0.5084812 0.9937670 0.2435521 0.2435521 0.257431653
226 -0.5101339 0.9995988 0.2427568 0.2427568 0.248105184
227 -0.4968128 0.9233276 0.2419872 0.2419872 0.256303014
228 -0.5189644 0.9540886 0.2411918 0.2411918 0.247424939
229 -0.5717991 0.9955963 0.2403964 0.2403964 0.202288722
230 -0.6249550 0.8928789 0.2396779 0.2396779 0.124043403
231 -0.6043398 0.8956156 0.2388826 0.2388826 0.154913515
232 -0.5392528 0.9159434 0.2381128 0.2381128 0.217932545
233 -0.4703113 1.0387347 0.2373174 0.2373174 0.265923985
234 -0.4425914 1.0318886 0.2365477 0.2365477 0.297016664
235 -0.4689731 1.0526166 0.2357523 0.2357523 0.302134598
236 -0.4552692 1.0100570 0.2349569 0.2349569 0.271562724
237 -0.5450581 1.0092252 0.2341872 0.2341872 0.247659441
238 -0.4732256 0.9981823 0.2333918 0.2333918 0.237783437
239 -0.4965476 0.9586184 0.2326220 0.2326220 0.248132389
240 -0.4995680 0.9142713 0.2318267 0.2318267 0.238672309
241 -0.5176974 0.9316808 0.2310313 0.2310313 0.195389564
242 -0.6462141 0.9147345 0.2303128 0.2303128 0.111617981
243 -0.5816463 0.8225454 0.2295175 0.2295175 0.145602865
244 -0.5750021 0.9436211 0.2287477 0.2287477 0.208639817
245 -0.4932050 0.9924028 0.2279523 0.2279523 0.257095497
246 -0.4355111 1.0537457 0.2271826 0.2271826 0.287538731
247 -0.4802542 1.0524359 0.2263872 0.2263872 0.292521550
248 -0.4780137 0.9613902 0.2255918 0.2255918 0.262379364
249 -0.4477351 0.9859161 0.2248221 0.2248221 0.237886126
250 -0.4891789 0.9995683 0.2240267 0.2240267 0.227495033
251 -0.5242338 0.9733901 0.2232569 0.2232569 0.239984500
252 -0.5363703 0.9075536 0.2224616 0.2224616 0.229915359
253 -0.5543496 0.9331444 0.2216662 0.2216662 0.188431523
254 -0.5686888 0.8920254 0.2209221 0.2209221 0.111424563
255 -0.6031192 0.8924101 0.2201267 0.2201267 0.136215277
256 -0.5031214 0.9538895 0.2193570 0.2193570 0.199084815
257 -0.4752052 0.9899952 0.2185616 0.2185616 0.246078815
258 -0.4864838 0.9890236 0.2177918 0.2177918 0.278412342
259 -0.5150226 1.0210628 0.2169964 0.2169964 0.283824534
260 -0.4954602 0.9939120 0.2162010 0.2162010 0.252421556
261 -0.5832138 0.9636245 0.2154313 0.2154313 0.229716327
262 -0.4944010 0.9931838 0.2146359 0.2146359 0.220973556
263 -0.5116574 0.9437888 0.2138662 0.2138662 0.227011765
264 -0.4934496 0.9829033 0.2130708 0.2130708 0.218688567
265 -0.5634236 0.8731522 0.2122754 0.2122754 0.171644583
266 -0.7138273 0.8413181 0.2115570 0.2115570 0.098989416
267 -0.5441964 0.8602875 0.2107616 0.2107616 0.126793703
268 -0.5674516 0.8979596 0.2099919 0.2099919 0.189756486
269 -0.4314097 1.0543086 0.2091965 0.2091965 0.237260604
270 -0.4835588 1.0463704 0.2084267 0.2084267 0.268983721
271 -0.4804370 0.9558227 0.2076313 0.2076313 0.274245013
272 -0.5076191 0.9321927 0.2068359 0.2068359 0.243252871
273 -0.5135441 0.9290961 0.2060662 0.2060662 0.219945785
274 -0.5389868 0.9248010 0.2052708 0.2052708 0.210619210
275 -0.5047113 0.9213165 0.2045011 0.2045011 0.218816939
276 -0.5693458 0.8601470 0.2037057 0.2037057 0.209938865
277 -0.5713267 0.9065359 0.2029103 0.2029103 0.164802648
278 -0.5924468 0.7883133 0.2021919 0.2021919 0.086557328
279 -0.6121604 0.8417274 0.2013965 0.2013965 0.117427441
280 -0.6072551 0.9107311 0.2006267 0.2006267 0.180446470
281 -0.4834577 0.9371544 0.1998314 0.1998314 0.228437910
282 -0.4596653 0.9641457 0.1990616 0.1990616 0.259530590
283 -0.4221470 0.9892599 0.1982662 0.1982662 0.264648524
284 -0.5276456 0.9903744 0.1974708 0.1974708 0.234076650
285 -0.4842598 0.9547471 0.1967011 0.1967011 0.210173367
286 -0.5088654 0.9384209 0.1959057 0.1959057 0.200297363
287 -0.5136624 0.9932709 0.1951360 0.1951360 0.210646315
288 -0.5555011 0.9060945 0.1943406 0.1943406 0.201186235
289 -0.5753485 0.9186126 0.1935452 0.1935452 0.157903490
290 -0.6739199 0.8240360 0.1928268 0.1928268 0.074131906
291 -0.6517911 0.7982201 0.1920314 0.1920314 0.108116791
292 -0.5278211 0.9163768 0.1912616 0.1912616 0.171153743
293 -0.4904655 0.9417439 0.1904662 0.1904662 0.219609423
294 -0.4949025 0.9949835 0.1896965 0.1896965 0.250052657
295 -0.4367288 1.0100345 0.1889011 0.1889011 0.255035476
296 -0.5103839 0.9777533 0.1881057 0.1881057 0.224893290
297 -0.5244061 0.9695019 0.1873360 0.1873360 0.200400051
298 -0.5466182 0.9142994 0.1865406 0.1865406 0.190008959
299 -0.5242771 0.9243894 0.1857709 0.1857709 0.202498425
300 -0.5455578 0.8960860 0.1849755 0.1849755 0.192429285
301 -0.5054091 0.8685106 0.1841801 0.1841801 0.150945449
302 -0.6496134 0.7728993 0.1834360 0.1834360 0.073938489
303 -0.5806042 0.8555883 0.1826406 0.1826406 0.098729202
304 -0.5631914 0.8693480 0.1818709 0.1818709 0.161598741
305 -0.5063742 0.9563184 0.1810755 0.1810755 0.208592741
306 -0.4999933 0.9268120 0.1803058 0.1803058 0.240926267
307 -0.4605083 1.0097009 0.1795104 0.1795104 0.246338460
308 -0.4942542 0.9537904 0.1787150 0.1787150 0.214935482
309 -0.5106866 0.9392903 0.1779452 0.1779452 0.192230252
310 -0.5484054 0.8948710 0.1771498 0.1771498 0.183487482
311 -0.5463044 0.9476523 0.1763801 0.1763801 0.189525691
312 -0.5424365 0.9476844 0.1755847 0.1755847 0.181202493
313 -0.5986077 0.8074867 0.1747893 0.1747893 0.134158509
314 -0.6988850 0.7854731 0.1740709 0.1740709 0.061503341
315 -0.6180520 0.8382449 0.1732755 0.1732755 0.089307629
316 -0.6301037 0.9228419 0.1725058 0.1725058 0.152270412
317 -0.5519388 0.9228517 0.1717104 0.1717104 0.199774530
318 -0.4417552 0.9965100 0.1709406 0.1709406 0.231497647
319 -0.5088441 0.9585780 0.1701453 0.1701453 0.236758938
320 -0.5535357 0.9238107 0.1693499 0.1693499 0.205766797
321 -0.4984347 0.8684608 0.1685801 0.1685801 0.182459711
322 -0.5531501 0.9004012 0.1677847 0.1677847 0.173133136
323 -0.5174796 0.9319850 0.1670150 0.1670150 0.181330865
324 -0.5316421 0.8721924 0.1669893 0.1669893 0.176783242
325 -0.5352489 0.8957410 0.1669637 0.1669637 0.172707529
326 -0.6114807 0.8909999 0.1669380 0.1669380 0.169174866
327 -0.5992742 0.9422430 0.1669124 0.1669124 0.166240151
328 -0.4998697 0.8975276 0.1668867 0.1668867 0.163940753
329 -0.5558289 0.8637514 0.1668611 0.1668611 0.162295748
330 -0.5823005 0.8431980 0.1668354 0.1668354 0.161305663
331 -0.5775569 0.9015486 0.1668097 0.1668097 0.160952767
332 -0.5665267 0.8910598 0.1667841 0.1667841 0.161201874
333 -0.5845577 0.8217209 0.1667584 0.1667584 0.162001654
334 -0.5636982 0.9006113 0.1667328 0.1667328 0.163286399
335 -0.5566092 0.9517460 0.1667071 0.1667071 0.164978199
336 -0.5041642 0.8972785 0.1666815 0.1666815 0.166989463
337 -0.5222340 0.9161680 0.1666558 0.1666558 0.169225706
338 -0.4878498 0.8981477 0.1666301 0.1666301 0.171588522
339 -0.5386896 0.9219667 0.1666045 0.1666045 0.173978658
340 -0.5200068 0.9296524 0.1665788 0.1665788 0.176299089
341 -0.4978766 0.8737547 0.1665532 0.1665532 0.178458005
342 -0.5779683 0.8658880 0.1665275 0.1665275 0.180371625
343 -0.6028638 0.9106728 0.1665018 0.1665018 0.181966743
344 -0.5760092 0.9169715 0.1664762 0.1664762 0.183182936
345 -0.5488136 0.8845244 0.1664505 0.1664505 0.183974362
346 -0.5825205 0.9262409 0.1664249 0.1664249 0.184311094
347 -0.5318800 0.9540880 0.1663992 0.1663992 0.184179941
348 -0.5277490 0.9130492 0.1663736 0.1663736 0.183584742
349 -0.5817848 0.9258964 0.1663479 0.1663479 0.182546102
350 -0.5827724 0.8457979 0.1663222 0.1663222 0.181100594
351 -0.5614056 0.8607998 0.1662966 0.1662966 0.179299430
352 -0.5580428 0.9130964 0.1662709 0.1662709 0.177206656
353 -0.6201965 0.8751503 0.1662453 0.1662453 0.174896907
354 -0.5964770 0.8737878 0.1662196 0.1662196 0.172452790
355 -0.5384468 0.8869195 0.1661940 0.1661940 0.169961988
356 -0.6269161 0.8681980 0.1661683 0.1661683 0.167514143
357 -0.6022832 0.9229905 0.1661426 0.1661426 0.165197640
358 -0.6272973 0.9444194 0.1661170 0.1661170 0.163096369
359 -0.5472338 0.9075124 0.1660913 0.1660913 0.161286585
360 -0.5218602 0.9153133 0.1660657 0.1660657 0.159833933
361 -0.5914933 0.8881061 0.1660400 0.1660400 0.158790775
362 -0.5886684 0.8566335 0.1660143 0.1660143 0.158193865
363 -0.5315946 0.9096364 0.1659887 0.1659887 0.158062478
364 -0.6157747 0.8496494 0.1659630 0.1659630 0.158397042
365 -0.5449525 0.9235041 0.1659374 0.1659374 0.159178335
366 -0.5866730 0.8690348 0.1659117 0.1659117 0.160367275
367 -0.5572654 0.8608415 0.1658861 0.1658861 0.161905326
368 -0.6039917 0.8804197 0.1658604 0.1658604 0.163715521
369 -0.5708778 0.8833938 0.1658347 0.1658347 0.165704084
370 -0.6319990 0.8841905 0.1658091 0.1658091 0.167762611
371 -0.5388858 0.8453396 0.1657834 0.1657834 0.169770776
372 -0.6295957 0.8780211 0.1657578 0.1657578 0.171599470
373 -0.6079812 0.8859728 0.1657321 0.1657321 0.173114311
374 -0.5360991 0.9320791 0.1657065 0.1657065 0.174179425
375 -0.5627453 0.9228403 0.1656808 0.1656808 0.174661397
376 -0.5542500 0.9185013 0.1656551 0.1656551 0.174433280
377 -0.5275690 0.8772301 0.1656295 0.1656295 0.173378556
378 -0.5942709 0.9049414 0.1656038 0.1656038 0.171394929
379 -0.5624841 0.8282051 0.1655782 0.1655782 0.168397848
380 -0.5858430 0.8879413 0.1655525 0.1655525 0.164323646
381 -0.6040385 0.9098090 0.1655268 0.1655268 0.159132211
382 -0.5545238 0.9033565 0.1655012 0.1655012 0.152809097
383 -0.6373020 0.8429010 0.1654755 0.1654755 0.145367007
384 -0.5336027 0.8751989 0.1654499 0.1654499 0.136846599
385 -0.6016026 0.8951533 0.1654242 0.1654242 0.127316574
386 -0.5440796 0.7940493 0.1653986 0.1653986 0.116873029
387 -0.6553166 0.8702757 0.1653729 0.1653729 0.105638090
388 -0.6772333 0.8544937 0.1653472 0.1653472 0.093757825
389 -0.5874730 0.8248707 0.1653216 0.1653216 0.081399506
390 -0.6657056 0.8020481 0.1652959 0.1652959 0.068748257
391 -0.6997825 0.8100705 0.1652703 0.1652703 0.056003182
392 -0.6819038 0.7627983 0.1652446 0.1652446 0.043373057
393 -0.7300284 0.8126819 0.1652190 0.1652190 0.031071694
394 -0.7045201 0.7763598 0.1651933 0.1651933 0.019313094
395 -0.7416101 0.7799718 0.1651676 0.1651676 0.008306502
396 -0.7718047 0.7556163 0.1651420 0.1651420 -0.001748499
397 -0.8090028 0.7486151 0.1651163 0.1651163 -0.010666732
398 -0.7823976 0.6858470 0.1650907 0.1650907 -0.018281898
399 -0.7028330 0.6905119 0.1650650 0.1650650 -0.024450635
400 -0.7611412 0.7395487 0.1650394 0.1650394 -0.029056087
401 -0.7921431 0.6709303 0.1650137 0.1650137 -0.032010862
402 -0.7954104 0.7514724 0.1649880 0.1649880 -0.033259314
403 -0.7590157 0.7056341 0.1649624 0.1649624 -0.032779089
404 -0.7611611 0.6896332 0.1649367 0.1649367 -0.030581879
405 -0.7821981 0.7331945 0.1649111 0.1649111 -0.026713374
406 -0.7913344 0.7393541 0.1648854 0.1648854 -0.021252403
407 -0.7329656 0.6808352 0.1648597 0.1648597 -0.014309279
408 -0.7724105 0.7161618 0.1648341 0.1648341 -0.006023403
409 -0.7235821 0.7636425 0.1648084 0.1648084 0.003439843
410 -0.6604281 0.7741591 0.1647828 0.1647828 0.013892805
411 -0.6797080 0.7637398 0.1647571 0.1647571 0.025129797
412 -0.7229463 0.7872455 0.1647315 0.1647315 0.036931767
413 -0.5951428 0.7736670 0.1647058 0.1647059 0.049071254
414 -0.6454741 0.7525723 0.1646801 0.1646802 0.061317538
415 -0.6877793 0.7579685 0.1646545 0.1646546 0.073441827
416 -0.6944620 0.8085106 0.1646288 0.1646289 0.085222378
417 -0.6725366 0.7750258 0.1646032 0.1646033 0.096449401
418 -0.7177484 0.8822232 0.1645775 0.1645777 0.106929650
419 -0.5888786 0.8688390 0.1645518 0.1645522 0.116490561
420 -0.6144840 0.8583787 0.1645261 0.1645266 0.124983860
421 -0.5445356 0.9129509 0.1645004 0.1645010 0.132288546
422 -0.5832955 0.9069301 0.1644747 0.1644755 0.138313179
423 -0.5375799 0.8646932 0.1644490 0.1644499 0.142997419
424 -0.5595157 0.8848715 0.1644233 0.1644242 0.146312799
425 -0.5516603 0.9009156 0.1643976 0.1643986 0.148262700
426 -0.5892554 0.9405642 0.1643719 0.1643729 0.148881565
427 -0.6115951 0.8674317 0.1643462 0.1643473 0.148233348
428 -0.6423815 0.9047397 0.1643205 0.1643217 0.146409281
429 -0.5878108 0.8746491 0.1642949 0.1642960 0.143524998
430 -0.5763258 0.9058103 0.1642692 0.1642704 0.139717120
431 -0.5320568 0.8565472 0.1642434 0.1642448 0.135139378
432 -0.5902985 0.8810796 0.1642177 0.1642191 0.129958396
433 -0.6076640 0.8489319 0.1641920 0.1641935 0.124349238
434 -0.6401301 0.8095654 0.1641663 0.1641679 0.118490840
435 -0.6290518 0.8163658 0.1641406 0.1641423 0.112561453
436 -0.6223387 0.8513715 0.1641149 0.1641166 0.106734207
437 -0.6200264 0.8260138 0.1640892 0.1640910 0.101172915
438 -0.6469698 0.8772955 0.1640635 0.1640655 0.096028222
439 -0.6078684 0.7742177 0.1640378 0.1640399 0.091434188
440 -0.6054831 0.8259783 0.1640121 0.1640143 0.087505398
441 -0.6397528 0.8066830 0.1639863 0.1639887 0.084334647
442 -0.6815879 0.8382684 0.1639606 0.1639631 0.081991275
443 -0.6143526 0.7941689 0.1639350 0.1639375 0.080520154
444 -0.6881529 0.7861129 0.1639093 0.1639119 0.079941366
445 -0.6749093 0.8058217 0.1638836 0.1638863 0.080250547
446 -0.6073093 0.8058595 0.1638579 0.1638607 0.081419883
447 -0.6052116 0.8466971 0.1638322 0.1638350 0.083399716
448 -0.6483776 0.8044061 0.1638065 0.1638094 0.086120698
449 -0.6671175 0.8321644 0.1637808 0.1637838 0.089496425
450 -0.6465667 0.8454335 0.1637552 0.1637583 0.093426465
451 -0.6368146 0.8702265 0.1637295 0.1637326 0.097799690
452 -0.5890523 0.8951934 0.1637038 0.1637070 0.102497812
453 -0.6781751 0.8772903 0.1636781 0.1636814 0.107399017
454 -0.6106684 0.8544408 0.1636525 0.1636559 0.112381590
455 -0.6210282 0.8021080 0.1636267 0.1636302 0.117327440
456 -0.5848081 0.8998639 0.1636010 0.1636046 0.122125417
457 -0.6289975 0.8753252 0.1635752 0.1635790 0.126674335
458 -0.5920106 0.8755138 0.1635495 0.1635534 0.130885616
459 -0.5904036 0.8984000 0.1635237 0.1635277 0.134685501
460 -0.5914630 0.8523335 0.1634980 0.1635022 0.138016761
461 -0.6179950 0.8372507 0.1634723 0.1634767 0.140839869
462 -0.5927824 0.8873363 0.1634465 0.1634511 0.143133626
463 -0.5926748 0.8783733 0.1634208 0.1634256 0.144895212
464 -0.4882066 0.9184819 0.1633950 0.1634001 0.146139696
465 -0.5857090 0.9597574 0.1633693 0.1633746 0.146899009
466 -0.6393742 0.8410997 0.1633436 0.1633490 0.147220441
467 -0.6034726 0.8502746 0.1633179 0.1633234 0.147164696
468 -0.5588160 0.9489025 0.1632922 0.1632978 0.146803596
469 -0.5674978 0.8733098 0.1632663 0.1632722 0.146217481
470 -0.5503472 0.8826495 0.1632406 0.1632466 0.145492410
471 -0.5616500 0.8867489 0.1632148 0.1632211 0.144717245
472 -0.5995543 0.8962992 0.1631890 0.1631955 0.143980699
473 -0.6155828 0.8733319 0.1631633 0.1631699 0.143368451
474 -0.5984058 0.8732178 0.1631375 0.1631443 0.142960396
475 -0.5184185 0.9216299 0.1631118 0.1631187 0.142828136
476 -0.6081289 0.9132202 0.1630860 0.1630931 0.143032756
477 -0.5437082 0.8682958 0.1630603 0.1630675 0.143622970
478 -0.6134756 0.8965355 0.1630346 0.1630419 0.144633673
479 -0.6087651 0.8173186 0.1630089 0.1630163 0.146084945
480 -0.6246802 0.9185223 0.1629832 0.1629908 0.147981531
481 -0.5478282 0.8874501 0.1629574 0.1629652 0.150312803
482 -0.4877246 0.8774848 0.1629316 0.1629396 0.153053196
483 -0.6206437 0.9276802 0.1629059 0.1629140 0.156163108
484 -0.5845258 0.8972962 0.1628802 0.1628885 0.159590225
485 -0.5649999 0.8995781 0.1628545 0.1628629 0.163271226
486 -0.5492772 0.9422112 0.1628287 0.1628373 0.167133813
487 -0.5236713 0.9383226 0.1628030 0.1628118 0.171098999
488 -0.6074896 0.9026655 0.1627773 0.1627862 0.175083589
489 -0.5861465 0.9242789 0.1627516 0.1627606 0.179002765
490 -0.5315445 0.9115297 0.1627259 0.1627350 0.182772707
491 -0.4940245 0.9773403 0.1627002 0.1627094 0.186313163
492 -0.5654472 0.9667427 0.1626744 0.1626838 0.189549896
493 -0.5057213 0.9531183 0.1626487 0.1626582 0.192416931
494 -0.5603480 0.9064249 0.1626230 0.1626326 0.194858538
495 -0.5020999 0.9324386 0.1625973 0.1626070 0.196830895
496 -0.5739389 0.9758319 0.1625716 0.1625816 0.198303378
497 -0.5430989 0.9376455 0.1625459 0.1625560 0.199259454
498 -0.5509408 0.9439107 0.1625200 0.1625303 0.199697140
499 -0.5175937 0.9717358 0.1624943 0.1625047 0.199629025
500 -0.5554716 0.8991875 0.1624685 0.1624791 0.199081860
501 -0.5680433 0.9154456 0.1624428 0.1624535 0.198095727
502 -0.5829789 0.9050856 0.1624171 0.1624279 0.196722813
503 -0.5667074 0.9444729 0.1623913 0.1624023 0.195025845
504 -0.5765045 0.9326198 0.1623656 0.1623767 0.193076209
505 -0.5233458 0.8962930 0.1623399 0.1623511 0.190951836
506 -0.5311945 0.8589712 0.1623142 0.1623255 0.188734906
507 -0.5600116 0.8885671 0.1622884 0.1622999 0.186509445
508 -0.4990729 0.9328636 0.1622623 0.1622743 0.184358889
509 -0.5568784 0.8815169 0.1622365 0.1622487 0.182363676
510 -0.5353219 0.8689412 0.1622108 0.1622231 0.180598958
511 -0.5343840 0.9189145 0.1621851 0.1621975 0.179132476
512 -0.5499276 0.9232573 0.1621593 0.1621720 0.178022682
513 -0.5756993 0.9065514 0.1621336 0.1621464 0.177317142
514 -0.5745253 0.9097509 0.1621079 0.1621209 0.177051276
515 -0.5229619 0.9307006 0.1620822 0.1620953 0.177247466
516 -0.5988682 0.9155909 0.1620564 0.1620697 0.177914559
517 -0.5733634 0.8815466 0.1620307 0.1620441 0.179047763
518 -0.5793985 0.9779871 0.1620050 0.1620185 0.180628950
519 -0.5211409 0.9125876 0.1619793 0.1619928 0.182627345
520 -0.5306225 0.9096453 0.1619535 0.1619672 0.185000576
521 -0.5041016 0.9318618 0.1619278 0.1619416 0.187696053
522 -0.5300197 0.8489184 0.1619021 0.1619160 0.190652632
523 -0.5448346 0.9243677 0.1618764 0.1618904 0.193802502
524 -0.5240187 0.9084441 0.1618507 0.1618649 0.197073257
525 -0.5408947 0.9032262 0.1618249 0.1618394 0.200390060
526 -0.4824457 0.9008044 0.1617992 0.1618138 0.203677864
527 -0.5770024 0.9233992 0.1617735 0.1617882 0.206863600
528 -0.5229782 0.9588803 0.1617478 0.1617626 0.209878281
529 -0.5213651 0.9289022 0.1617221 0.1617370 0.212658951
530 -0.4805584 0.9165172 0.1616964 0.1617115 0.215150431
531 -0.4945587 0.9512587 0.1616707 0.1616859 0.217306807
532 -0.5159767 0.9146246 0.1616450 0.1616603 0.219092619
533 -0.5140694 0.9206543 0.1616193 0.1616347 0.220483723
534 -0.4810278 0.9305676 0.1615935 0.1616091 0.221467803
535 -0.5328131 0.9313849 0.1615677 0.1615836 0.222044516
536 -0.5298218 0.8892018 0.1615420 0.1615581 0.222225277
537 -0.5138909 0.9650824 0.1615162 0.1615325 0.222032704
538 -0.4724618 0.9314860 0.1614905 0.1615069 0.221499718
539 -0.4964121 0.9126072 0.1614648 0.1614813 0.220668359
540 -0.5153104 0.9178972 0.1614391 0.1614557 0.219588340
541 -0.5042045 0.9778742 0.1614134 0.1614302 0.218315395
542 -0.4944714 0.9020834 0.1613876 0.1614046 0.216909462
543 -0.5322113 0.9024247 0.1613618 0.1613790 0.215432780
544 -0.5059730 0.9112572 0.1613360 0.1613534 0.213947935
545 -0.4814716 0.9896889 0.1613104 0.1613280 0.212515930
546 -0.4758440 0.9373106 0.1612846 0.1613025 0.211194340
547 -0.5192876 0.9357866 0.1612589 0.1612770 0.210035590
548 -0.5087076 0.9141248 0.1612331 0.1612514 0.209085429
549 -0.5609982 0.9470829 0.1612073 0.1612259 0.208381629
550 -0.5772879 0.9186813 0.1611816 0.1612003 0.207952946
551 -0.4995782 0.9721974 0.1611558 0.1611747 0.207818385
552 -0.5471499 0.9030511 0.1611301 0.1611492 0.207986765
553 -0.5614192 0.9278490 0.1611043 0.1611236 0.208456622
554 -0.5843622 0.9191335 0.1610786 0.1610980 0.209216415
555 -0.5119986 0.9640041 0.1610528 0.1610725 0.210245049
556 -0.5148946 0.9430648 0.1610271 0.1610469 0.211512691
557 -0.4872838 0.9894724 0.1610013 0.1610213 0.212981832
558 -0.5443284 0.9032159 0.1609755 0.1609957 0.214608579
559 -0.5347758 0.9225350 0.1609498 0.1609702 0.216344126
560 -0.5180573 0.9469174 0.1609240 0.1609447 0.218136345
561 -0.5891298 1.0027034 0.1608982 0.1609191 0.219931461
562 -0.5092678 0.9516958 0.1608725 0.1608936 0.221675752
563 -0.5018154 0.9465061 0.1608467 0.1608680 0.223317209
564 -0.5277846 0.9750085 0.1608210 0.1608424 0.224807118
565 -0.5209415 0.9294018 0.1607952 0.1608168 0.226101514
566 -0.4854944 0.9488438 0.1607695 0.1607913 0.227162450
567 -0.5163691 0.9253845 0.1607437 0.1607657 0.227959056
568 -0.5292690 1.0084222 0.1607180 0.1607401 0.228468356
569 -0.4986343 0.9484932 0.1606922 0.1607145 0.228675807
570 -0.5251587 0.9644131 0.1606665 0.1606889 0.228575568
571 -0.5553138 0.9906098 0.1606408 0.1606633 0.228170476
572 -0.4578081 0.9960348 0.1606150 0.1606377 0.227471742
573 -0.5211599 0.9323225 0.1605892 0.1606121 0.226498384
574 -0.4671862 1.0134340 0.1605634 0.1605865 0.225276407
575 -0.4972006 0.9836023 0.1605376 0.1605610 0.223837779
576 -0.5258106 1.0085860 0.1605119 0.1605355 0.222219219
577 -0.5034787 0.9478631 0.1604861 0.1605100 0.220460856
578 -0.4703580 0.9741532 0.1604604 0.1604844 0.218604799
579 -0.5097865 1.0118463 0.1604345 0.1604588 0.216693661
580 -0.5168456 0.9151718 0.1604086 0.1604333 0.214769101
581 -0.5201455 1.0271211 0.1603827 0.1604078 0.212870421
582 -0.5008781 0.9536263 0.1603568 0.1603823 0.211033267
583 -0.5654311 0.9232483 0.1603309 0.1603568 0.209288481
584 -0.5426008 0.9309631 0.1603051 0.1603313 0.207661139
585 -0.5466747 0.9325510 0.1602793 0.1603058 0.206169810
586 -0.5191469 0.9479472 0.1602534 0.1602802 0.204826049
587 -0.5522489 0.9079971 0.1602276 0.1602546 0.203634155
588 -0.5156634 0.9572022 0.1602018 0.1602290 0.202591193
589 -0.5735246 0.9382488 0.1601760 0.1602034 0.201687269
590 -0.5528608 0.9511594 0.1601503 0.1601778 0.200906067
591 -0.4956211 0.9569846 0.1601246 0.1601522 0.200225617
592 -0.5697004 0.9090486 0.1600987 0.1601268 0.199619256
593 -0.4778447 0.8723058 0.1600728 0.1601013 0.199056778
594 -0.5478318 0.8999491 0.1600471 0.1600758 0.198505698
595 -0.5771520 0.9307282 0.1600213 0.1600502 0.197932613
596 -0.5251222 0.9330689 0.1599956 0.1600246 0.197304595
597 -0.5850000 0.9103008 0.1599699 0.1599990 0.196590576
598 -0.5250345 0.9145501 0.1599442 0.1599734 0.195762676
599 -0.4997756 0.9027200 0.1599184 0.1599480 0.194797421
600 -0.5525329 0.9703331 0.1598925 0.1599224 0.193676810
601 -0.5616788 0.9601744 0.1598667 0.1598972 0.192389197
602 -0.5429918 0.9314371 0.1598408 0.1598716 0.190929947
603 -0.5618230 0.9216311 0.1598151 0.1598460 0.189301848
604 -0.5607199 0.9146626 0.1597893 0.1598205 0.187515251
605 -0.5294817 0.8934788 0.1597636 0.1597949 0.185587947
606 -0.5339693 0.9437288 0.1597378 0.1597693 0.183544765
607 -0.5378933 0.8882893 0.1597121 0.1597437 0.181416900
608 -0.5723867 0.9637070 0.1596862 0.1597181 0.179241014
609 -0.5781270 0.9591137 0.1596605 0.1596925 0.177058101
610 -0.5550071 0.8463032 0.1596347 0.1596671 0.174912184
611 -0.5690192 0.9294078 0.1596090 0.1596416 0.172848862
612 -0.5922589 0.8667212 0.1595832 0.1596162 0.170913770
613 -0.5415242 0.8830583 0.1595575 0.1595908 0.169150990
614 -0.5719167 0.9133583 0.1595317 0.1595653 0.167601478
615 -0.5888858 0.8714572 0.1595060 0.1595399 0.166301544
616 -0.5605330 0.9056652 0.1594803 0.1595142 0.165281462
617 -0.5975910 0.9031961 0.1594545 0.1594887 0.164564233
618 -0.5482402 0.9359748 0.1594287 0.1594632 0.164164561
619 -0.5554707 0.9168189 0.1594028 0.1594376 0.164088079
620 -0.6070683 0.8649276 0.1593770 0.1594120 0.164330856
621 -0.6398891 0.9040108 0.1593513 0.1593864 0.164879201
622 -0.5756520 0.9040870 0.1593255 0.1593609 0.165709792
623 -0.6309495 0.9062352 0.1592998 0.1593353 0.166790114
624 -0.5733473 0.9234174 0.1592740 0.1593097 0.168079223
625 -0.5497221 0.9395062 0.1592482 0.1592841 0.169528792
626 -0.5546857 0.9341533 0.1592224 0.1592586 0.171084442
627 -0.5243937 0.9101045 0.1591966 0.1592330 0.172687293
628 -0.5356600 0.9283462 0.1591707 0.1592075 0.174275713
629 -0.5924443 0.8676256 0.1591449 0.1591820 0.175787208
630 -0.5627085 0.8729734 0.1591191 0.1591565 0.177160385
631 -0.4888007 0.9370374 0.1590933 0.1591310 0.178336948
632 -0.5697859 0.8630337 0.1590674 0.1591055 0.179263651
633 -0.4876073 0.9933621 0.1590416 0.1590799 0.179894148
634 -0.5705867 0.8529934 0.1590156 0.1590544 0.180190685
635 -0.5431930 0.9296854 0.1589898 0.1590289 0.180125572
636 -0.5133784 0.9193165 0.1589640 0.1590034 0.179682387
637 -0.5810205 0.9747930 0.1589383 0.1589781 0.178856867
638 -0.5262400 0.9459708 0.1589124 0.1589528 0.177657453
639 -0.5501251 0.8964713 0.1588866 0.1589273 0.176105464
640 -0.5366194 0.9192033 0.1588609 0.1589018 0.174234876
641 -0.5446153 0.9184511 0.1588352 0.1588762 0.172091725
642 -0.5380657 0.8968893 0.1588094 0.1588506 0.169733118
643 -0.5440048 0.9528737 0.1587837 0.1588250 0.167225886
644 -0.5534801 0.8925975 0.1587579 0.1587995 0.164644918
645 -0.5560942 0.9057922 0.1587321 0.1587740 0.162071194
646 -0.6020088 0.8795310 0.1587064 0.1587486 0.159589597
647 -0.5546814 0.8852867 0.1586805 0.1587231 0.157286540
648 -0.5174767 0.9266168 0.1586546 0.1586977 0.155247494
649 -0.5795304 0.9185314 0.1586287 0.1586722 0.153554465
650 -0.5547100 0.8218813 0.1586027 0.1586467 0.152283521
651 -0.5826714 0.9003309 0.1585769 0.1586211 0.151502408
652 -0.5463947 0.8747567 0.1585512 0.1585956 0.151268358
653 -0.5549589 0.8578609 0.1585254 0.1585700 0.151626140
654 -0.6079942 0.9055237 0.1584997 0.1585445 0.152606410
655 -0.5541872 0.9234090 0.1584740 0.1585190 0.154224431
656 -0.5368677 0.8239974 0.1584482 0.1584935 0.156479190
657 -0.5489738 0.9036674 0.1584225 0.1584680 0.159352956
658 -0.5795663 0.8801407 0.1583967 0.1584425 0.162811289
659 -0.5335122 0.9165645 0.1583710 0.1584170 0.166803518
660 -0.5675715 0.8875696 0.1583453 0.1583915 0.171263679
661 -0.5391164 0.9379361 0.1583195 0.1583660 0.176111887
662 -0.5508795 0.9265663 0.1582938 0.1583405 0.181256125
663 -0.5792637 0.8908064 0.1582680 0.1583150 0.186594387
664 -0.5330498 0.9013617 0.1582423 0.1582894 0.192017140
665 -0.5300117 0.9355487 0.1582166 0.1582638 0.197410027
666 -0.5376420 0.9684912 0.1581908 0.1582383 0.202656741
667 -0.5271021 0.9301219 0.1581651 0.1582129 0.207641997
668 -0.5062564 1.0024788 0.1581393 0.1581874 0.212254514
669 -0.5027386 0.9502962 0.1581134 0.1581619 0.216389934
670 -0.5235918 1.0328003 0.1580875 0.1581364 0.219953578
671 -0.5208409 0.9570398 0.1580616 0.1581109 0.222862982
672 -0.4619228 1.0096795 0.1580357 0.1580854 0.225050129
673 -0.5467014 0.9954155 0.1580099 0.1580600 0.226463305
674 -0.5057284 0.9323103 0.1579839 0.1580345 0.227068547
675 -0.4824857 0.9485611 0.1579579 0.1580090 0.226850614
676 -0.5039320 0.9526956 0.1579319 0.1579833 0.225813465
677 -0.5110520 0.9578170 0.1579061 0.1579576 0.223980228
678 -0.5084078 0.9600662 0.1578803 0.1579320 0.221392647
679 -0.4918586 0.9532098 0.1578545 0.1579065 0.218110035
680 -0.5195509 0.9198183 0.1578287 0.1578810 0.214207741
681 -0.4974367 0.9796881 0.1578031 0.1578554 0.209775186
682 -0.4841804 0.9355829 0.1577774 0.1578299 0.204913519
683 -0.5985404 0.9557454 0.1577515 0.1578044 0.199732946
684 -0.5547572 0.8782330 0.1577255 0.1577789 0.194349823
685 -0.5401738 0.9502078 0.1576996 0.1577534 0.188883572
686 -0.5432949 0.9666457 0.1576739 0.1577279 0.183453534
687 -0.6045505 0.8906519 0.1576481 0.1577024 0.178175814
688 -0.5219990 0.8799955 0.1576224 0.1576769 0.173160241Multi Step Ahead Forecasts
Background
Let’s define Static and Dynamic multi step ahead forecasts.
- Static Forecast:
- Train = 1990-2000. Test = 2001 (1 step ahead)
- Train = 1990-2000. Test = 2002 (2 step ahead)
- Dynamic Forecast:
- Train = 1990-2000. Test = 2001 (1 step ahead)
- Train = 1990-2000 & 2001 Forecast. Test = 2002 (1 step ahead)
Notice that static forecasts successively further into the future, which can be difficult. Meanwhile, dynamic forecasts build upon potentially error-prone prior forecasts, which can be equally troublesome.
Notice pure distributed lag models (i.e. \(Y_{t}=\alpha + \beta X_{t-1}+u_{T]\)}) don’t permit dynamic forecasts since they require a forecast of \(X\). Moreover, distributed lag models only permit static forecasts up util the horizon of the \(X\) lag (i.e. one in this case).
Forecasts
Let’s use our training set, which ended in Dec2013 to create a series of 24 static forecasts (ie through the end of 2015).
### ARIMA
ARIMA_mulpred <- ts(forecast(ARIMA_auto, h = 24)$mean, start = c(2014,1), frequency =12)
### ARMA-ARCH
Garch_mulpred <- ts(fitted(ugarchforecast(fitORspec = garch_fit, n.ahead = 24)), start = c(2014,1), frequency =12)
### Holt-Winter
HW1_mulpred <- ts(forecast(HW1, h = 24)$mean, start = c(2014,1), frequency =12)
### NNET
NNET_mulpred <- ts(forecast(NNET, h = 24)$mean, start = c(2014,1), frequency =12)
### Random Forest
# We will need to write a loop to get static multiple step ahead forecast
h <- 24
RF_mulpred <- matrix(NA, h, 1)
X_multest <- head(X_test,1)
for (i in 1:h){
set.seed(123)
RF_mulpred[i] <- predict(RF_fit, X_multest)
X_multest[2:ncol(X_multest)] <- X_multest[-ncol(X_multest)] # update the "regressor" with predicted value
X_multest[1] <- RF_mulpred[i]
}
RF_mulpred <- ts(RF_mulpred, start = c(2014,1), frequency = 12)
### Prophet
df_prophet <- Prophet_traindata %>%
select(-HousingStartGrowth) %>%
rename(ds = Date) %>%
rename(y = PriceIndexGrowthSA)
m <- prophet(df_prophet)
future <- make_future_dataframe(m, periods = 24, freq = "month")
forecast <- predict(m, future)
fcst <- forecast[324:nrow(forecast),]
Prophet_mulpred <- ts(fcst[[16]], start = c(2014, 1), frequency = 12)
### Plot Forecast
Test<-window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014, 1), end=c(2015,12))
mulpreds <- ts.union(ARIMA_mulpred, Garch_mulpred, HW1_mulpred, NNET_mulpred, RF_mulpred, Prophet_mulpred, Test) %>%
`colnames<-`(c("ARMA","ARMA-GARCH","Holt Winters", "NNETAR", "Random Forest", "Prophet", "TestSample"))
autoplot(mulpreds) +
labs(color ='', y = "Forecast", x = '', title = "Static 24-Step Ahead Forecast")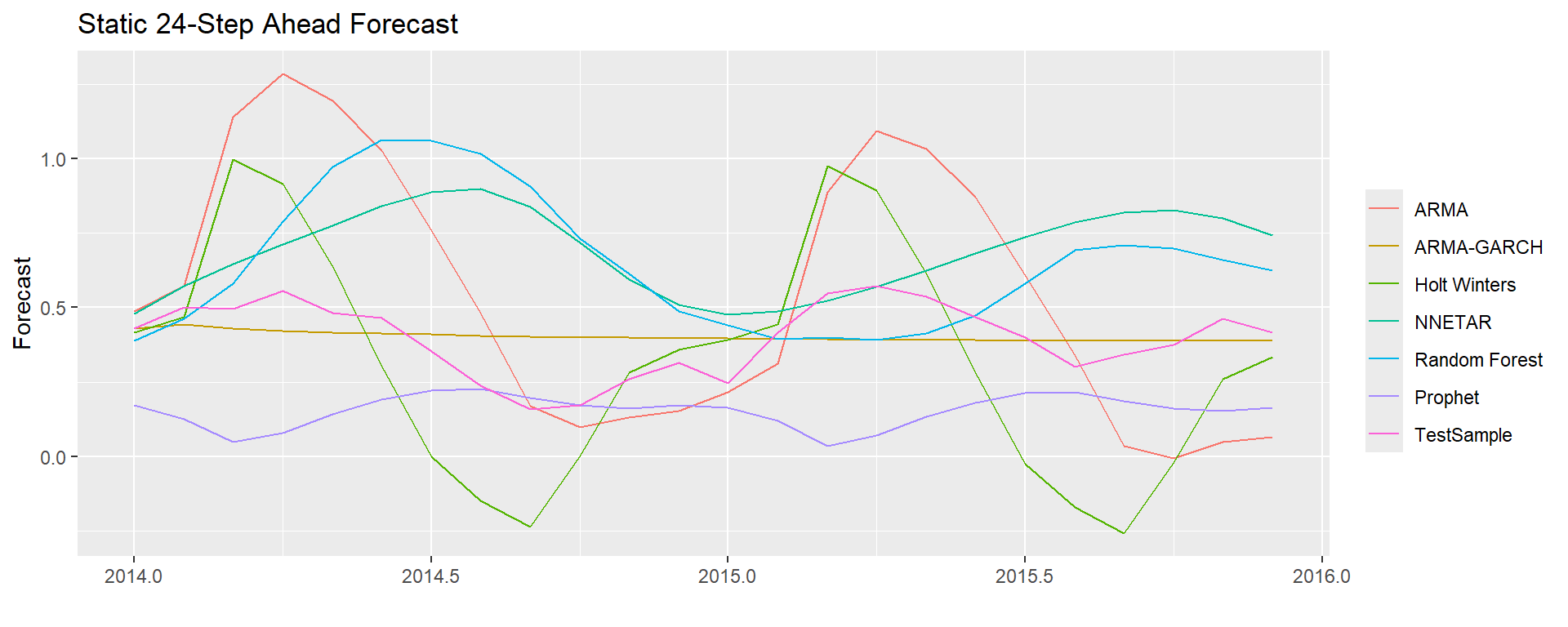
Forecast evaluation
Let’s compute the out of sample (OOS) forecast errors
errOOS <- ts((window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014, 1)) - mulpreds[,-7]),
start = c(2014,1), frequency =12)%>%
`colnames<-`(c("ARMA","ARMA-GARCH","Holt Winters", "NNETAR", "Random Forest", "Prophet"))We can summarize the errors
summary(errOOS) ARMA ARMA-GARCH Holt Winters NNETAR
Min. :-0.72971 Min. :-0.245062 Min. :-0.50130 Min. :-0.67980
1st Qu.:-0.42728 1st Qu.:-0.084840 1st Qu.:-0.09448 1st Qu.:-0.45889
Median :-0.06418 Median : 0.015699 Median : 0.05762 Median :-0.30968
Mean :-0.14537 Mean :-0.006291 Mean : 0.07481 Mean :-0.29318
3rd Qu.: 0.11060 3rd Qu.: 0.068342 3rd Qu.: 0.36231 3rd Qu.:-0.13534
Max. : 0.41304 Max. : 0.180014 Max. : 0.60161 Max. : 0.02495
Random Forest Prophet
Min. :-0.777501 Min. :-0.03806
1st Qu.:-0.416747 1st Qu.: 0.12301
Median :-0.201869 Median : 0.25425
Mean :-0.251776 Mean : 0.24130
3rd Qu.: 0.001816 3rd Qu.: 0.34774
Max. : 0.181093 Max. : 0.51082 Let’s construct the Mean Squared Forecast Error (MSFE).
MSFE<-colMeans(errOOS^2,na.rm = TRUE)
MSFE ARMA ARMA-GARCH Holt Winters NNETAR Random Forest
0.14293681 0.01354611 0.09195907 0.12603314 0.14212549
Prophet
0.08302371 Q: Comment on the accuracy of the models.
A:
- ARMA-GARCH is a clear winner to the other models.
- The complex Neural Net, Prophet, and RF behave about equally to each other.
Simulation
There are many uses of simulation in a time series context.
Parametric simulation (i.e. Monte Carlo) is often used when you have a good sense of the DGP. Meanwhile, non parametric simulation (i.e. Bootstrapping) relies upon successive draws of the empirical distribution.
In the following we will demonstrate using bootstrapping for construction forecast confidence intervals.
Bootstrapping Time Series
Recall that bootstrapping randomly resamples from the observed dataset in order to create many pseudo samples for analysis. The model of interest is implemented on each pseudo sample. The range of the resulting estimates provides a confidence interval for the estimation on the observed sample.
Unfortunately, random resampling disrupts the temporal persistence of the process. So, we rely upon block bootstrapping. Briefly, suppose your EDA suggests that the series has a temporal persistence of 12 months. Then we resample from the observed data by drawing blocks of 12 successive months. We can stitch these blocks together to generate a a pseudo sample of the desired size.
Create Block Bootstrap Samples
Note that due to the simulation process the pseudo samples you draw may be different each time. Best practice is to draw several hundred (or thousand) pseudo samples. For illustratives purpose, we’re only drawing for 4 pseudo samples here.
nT = nrow(df_adjts)
Train = window(df_adjts[,"PriceIndexGrowthSA"], end = c(2013,12))
Test = window(df_adjts[,"PriceIndexGrowthSA"], start = c(2014, 1))
TrainNum <- round(length(Train))
BootpathNum = 4
BootSamples <- bld.mbb.bootstrap(Train, BootpathNum,block_size=12) %>% data.frame() %>% ts(end= end(Train), frequency=12)
colnames(BootSamples) <- c(lapply(1:(BootpathNum), FUN =function(x){paste("Path",x,sep="")}))
plot(BootSamples, main = "Bootstrapped Samples")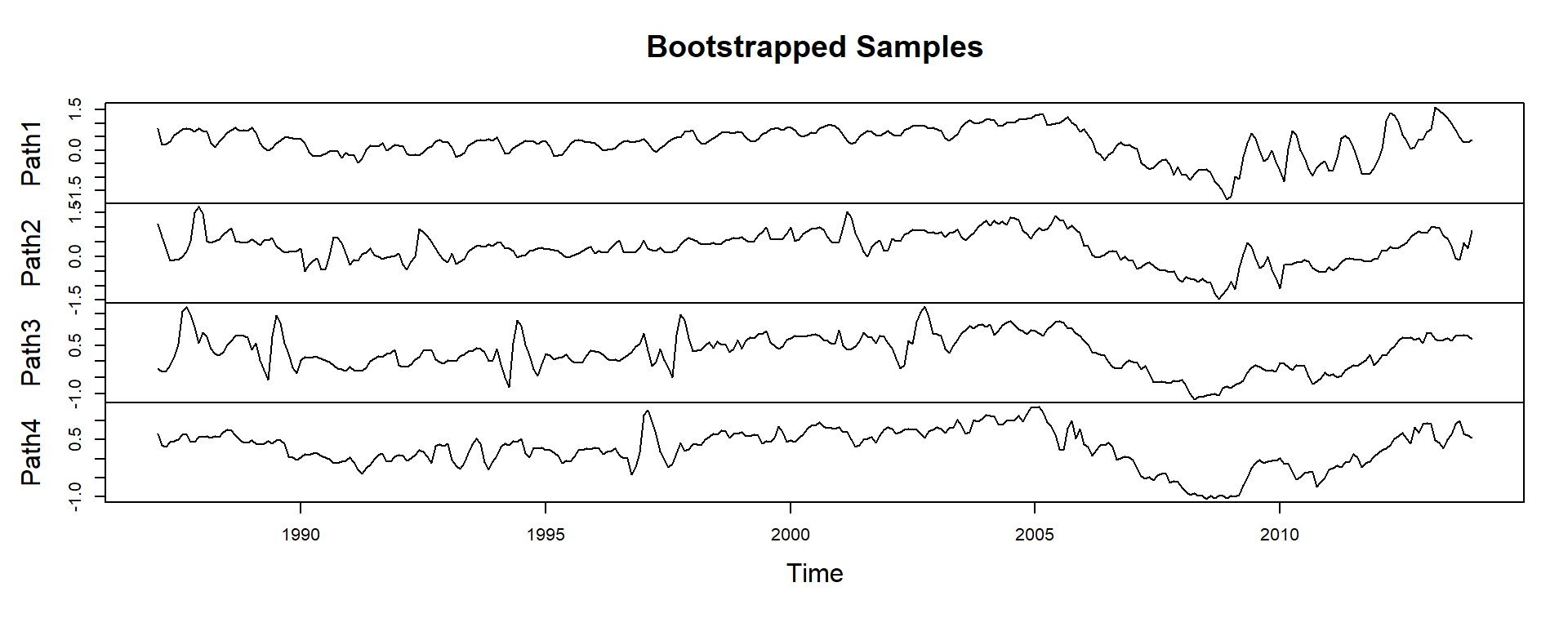
Bootstrapping for a Confidence Interval
Our goal here is to form a confidence interval around our forecast. We want to avoid making distributional assumptions, so we rely upon bootstraps.
Fit an ARIMA to Training Sample
ARMA_fit <- auto.arima(Train)
arimafc <- forecast(ARMA_fit, h=nT-TrainNum, level=95)
arimafc_err <- df_adjts[,"PriceIndexGrowthSA"] - arimafc$meanForecast on each Pseudo Sample
Use that fitted model specification and parameter estimates to construct forecasts for each bootstrap sample.
Bootfcast <- matrix(0, nrow=BootpathNum, ncol=nT-TrainNum)
for(i in seq(BootpathNum)) {
ARMA_refit <- Arima(BootSamples[,i], model=ARMA_fit) # fit model to bootstrapped samples without re-estimating
Bootfcast[i,] <- forecast(ARMA_refit, h = nT-TrainNum)$mean}Gather the Forecasts
We will gather all of the forecasts for Jan2014, and compute the 2.5% and 97.5% quantiles, which will serve to form a 95% confidence interval. Then repeat that for Feb2014, etc…
bootfc <- structure(list(
mean = ts(colMeans(Bootfcast), start = start(Test), frequency=12),
lower = ts(apply(Bootfcast, 2, quantile, prob=0.025), start = start(Test), frequency=12),
upper = ts(apply(Bootfcast, 2, quantile, prob=0.975), start = start(Test), frequency=12),
level = 95),
class="forecast"){plot(bootfc, xlim = c(1988,2023),main="Bootstrap Forecasts", shadecols = "gray70",fcol = NA)
lines(df_adjts[,"PriceIndexGrowthSA"], col = "black", lty = 2)
legend("bottomleft",legend=c("Raw Data","Bootstrapped Confidence Interval"),
col=c("black","grey70"), lty=c(2,1), lwd = c(1,4), cex=0.8, box.lty=0)}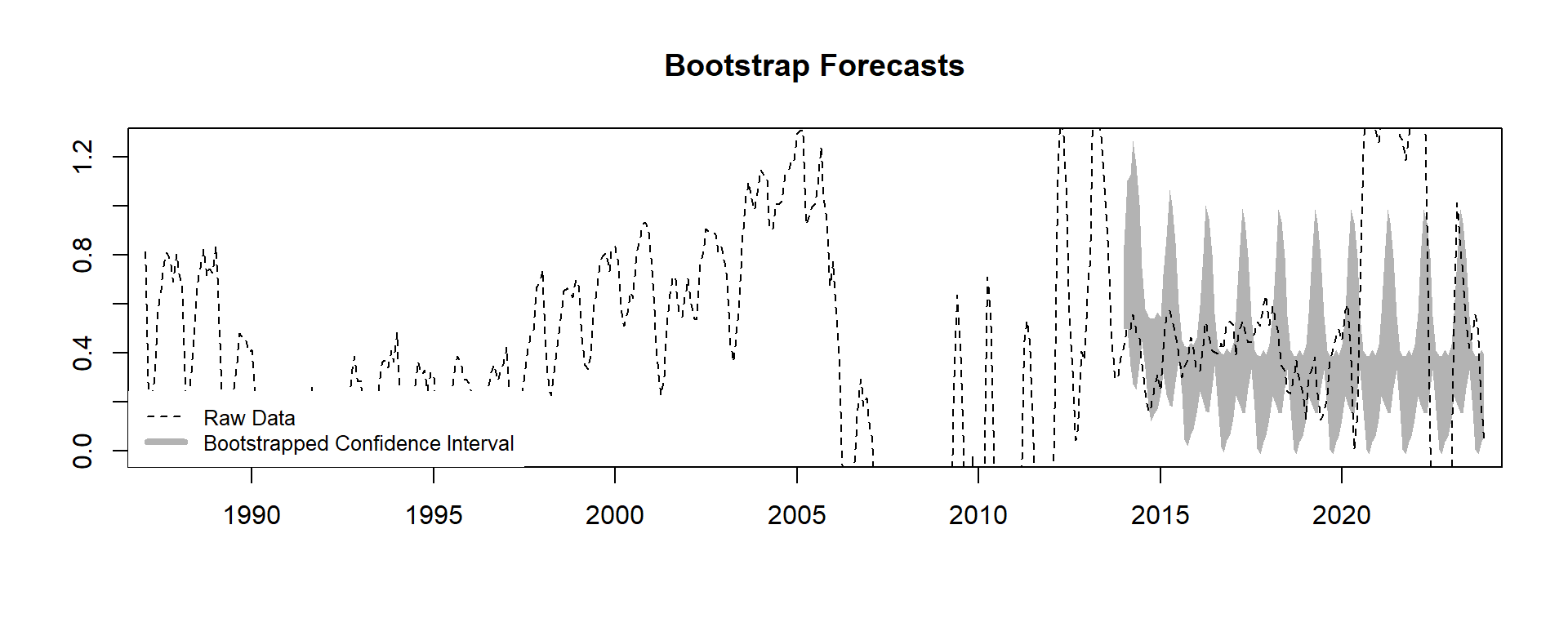
Q: Interpret the period just after 2020.
A:
- The gray region illustrates the range of the 95% forecast interval.
- Notice the large spike of the black line outside of the gray near the end of the sample after 2020.
- That implies our series experienced a “rare” event (e.g. price changes around COVID)
Bootstrap Aggregating (Bagging)
Aggregate forecasts across bootstrap sample (aka “bagging”) can be used to improve forecast accuracy by reducing one or more sources of uncertainty. Consider:
- Parameter Uncertainty — e.g. is \(\hat{\beta}\) correct?
- Model Uncertainty — e.g should I use ARMA(1,1) or ARMA(3,2) when I train?
Note: the term model uncertainty sometimes is decomposed to mean the proper model within the training period and stability of the DGP into the out of sample period.
Bagging can help to ameliorate parameter and model uncertainty.
Let’s say we found that an ARMA(1,1) was optimal for our series in the training period and we estimate the parameters \(\Theta_{ARMA(1,1)}\)
Case 1: Produce 1000s of bootstrap paths. For each path, forecast the series using the same \(\Theta_{ARMA(1,1)}\).
Q: What kind of uncertainty does Case 1 face?
A: All 3 types. We are using the same parameters and same model order.
Case 2: Produce 1000s of bootstrap paths. For each path \(h\), refit an optimal ARMA(1,1), yielding \(\Theta^{h}_{ARMA(1,1)}\)
Q: What kind of uncertainty does Case 2 face?
A: We have reduced parameter uncertainty, but we aren’t sure if we have the right model.
Case 3: Produce 1000s of bootstrap paths. For each path \(h\), refit an optimal ARMA(p,q), yielding \(\Theta^{h}_{ARMA(p,q)}\)
Q: What kind of uncertainty does Case 3 face?
A: We have reduced model and parameter uncertainty.
In the following we will illustrate Case 2 and Case 3 and compare to the single ARMA fit as our proxy for Case 1.
Bagging-Case 2
We will find the optimal functional form via information criterion.
We will then fit this functional form to each bootstrap sample, and then forecast. In doing so, the ARMA order remains the same, but the parameter estimates are optimized for each bootstrap path.
ARMA_fit <- auto.arima(Train) # optimal ARIMA is ARIMA(2,0,2)(0,1,2)[12]
bagfcast1 <- matrix(0, nrow=BootpathNum, ncol=nT-TrainNum)
for(i in seq(BootpathNum)) {
ARMA_refit <- Arima(BootSamples[,i],
order=c(2, 0, 2),
seasonal = list(order = c(0,1,2), period = 12)) # fitted ARIMA(2,0,2)(0,1,2)[12] with re-estimating
bagfcast1[i,] <- forecast(ARMA_refit, h = nT-TrainNum)$mean} %>% ts(frequency=12, start = start(Test))Bagging-Version 2
We will find the optimal ARIMA structure for each bootstrap path, fit the ARMA model accordingly, and then forecast.
bagfcast2 <- matrix(0, nrow=BootpathNum, ncol=nT-TrainNum)
for(i in seq(BootpathNum)) {
ARMA_refit <- auto.arima(BootSamples[,i]) # fitted optimal arima model with each sample
bagfcast2[i,] <- forecast(ARMA_refit, h = nT-TrainNum)$mean} Compare with (Non) Bagging
Let’s generate bagging forecast errors in the testing period.
bagfc1 <- colMeans(bagfcast1) %>% ts(frequency=12, start = start(Test))
bagfc2 <- colMeans(bagfcast2) %>% ts(frequency=12, start = start(Test))
bagfc1_err <- df_adjts[,"PriceIndexGrowthSA"] - bagfc1
bagfc2_err <- df_adjts[,"PriceIndexGrowthSA"] - bagfc2Now compare the forecast errors built from the optimal arima forecast, bootstrapped forecast, bagging1 and bagging2 forecast errors
{plot(arimafc_err, col = "red", xlab = "", ylab = "OOS Error", main = "ARIMA OOS Forecast Error")
lines(bagfc1_err, col = "green", lty = 3)
lines(bagfc2_err, col = "purple", lty = 4)
legend("bottomleft",legend=c("ARIMA Forecast OOS Error",
"Bagging Case 2 (Reduce Parameter Uncertainty)",
"Bagging case 3 (Reduce Parameter and Model Uncertainty)"),
col=c("red", "green","purple"), lty=c(1,2,3,4), cex=0.6, box.lty=0)
}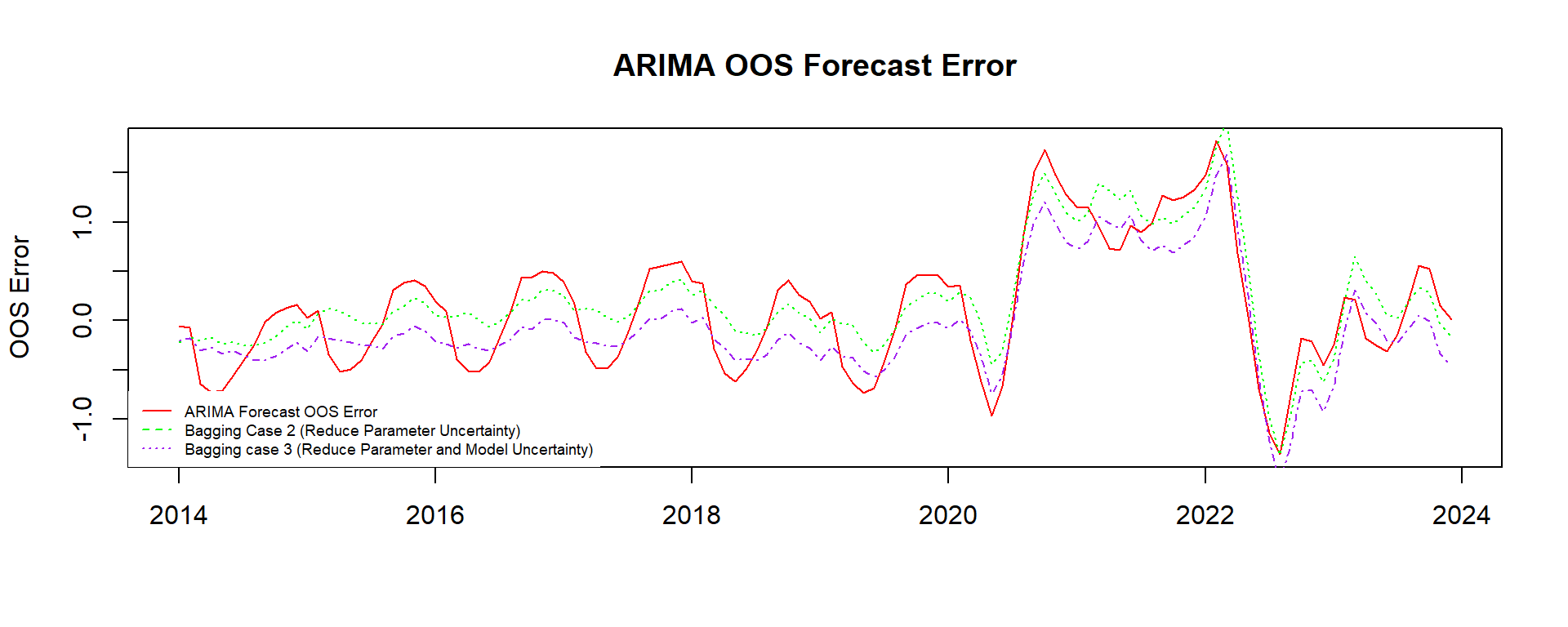
Q: Comment on the OOS Errors
A:
- Bagging was able to improve upon the ARMA model
- We were able to reduce parameter and model uncertainty in Cases 2 and 3, respectively
- Notice again the poor fit around COVID. Simply using temporal persistence is not able to capture this exogenous shock
VAR
Recall our earlier discussion where housing starts may both lead and lag price growth.
Economically, it might be that rapid housing starts signal more supply, which depresses prices.
Conversely, starts may be rising because prices are rising, which signal more profitability.
This simultaneity will bias coefficient estimates of our univariate specifications. Instead, we might consider a simultaneous system of autoregressive specifications; i.e. a vector auto regression VAR.
VAR tools are helpful for
- Causal estimation / inference
- Multivariate forecasting
- Stress testing
A VAR is an Autoregressive model across multiple series. e.g. housing starts are a function of past starts and prices; meanwhile prices may be a function of past prices and starts.
Lag Selection
We can rely upon information criterion to guide our choice of lag structure.
library(vars)
VAR_data<-window(df_adjts[,c("PriceIndexGrowthSA","HousingStartGrowth")], end = c(2013,12))
VARselect(VAR_data, lag.max = 12, type = "const", season = 12)$selectionAIC(n) HQ(n) SC(n) FPE(n)
12 2 2 12 The AIC suggests 12 lags.
Q: Why do we usually shun VAR of high order (i.e. a large number of lags)?
A:
- The number of parameters proliferate quickly in a VAR.
- In our case, we will start with 2 lags, as indicated by other criterion above
Fitting a VAR
VAR_est <- VAR(y = VAR_data, p = 2, type = "const")
summary(VAR_est)
VAR Estimation Results:
=========================
Endogenous variables: PriceIndexGrowthSA, HousingStartGrowth
Deterministic variables: const
Sample size: 321
Log Likelihood: -1213.088
Roots of the characteristic polynomial:
0.8271 0.396 0.396 0.1464
Call:
VAR(y = VAR_data, p = 2, type = "const")
Estimation results for equation PriceIndexGrowthSA:
===================================================
PriceIndexGrowthSA = PriceIndexGrowthSA.l1 + HousingStartGrowth.l1 + PriceIndexGrowthSA.l2 + HousingStartGrowth.l2 + const
Estimate Std. Error t value Pr(>|t|)
PriceIndexGrowthSA.l1 1.2891833 0.0504507 25.553 < 2e-16 ***
HousingStartGrowth.l1 0.0010618 0.0008132 1.306 0.19262
PriceIndexGrowthSA.l2 -0.3874746 0.0503866 -7.690 1.88e-13 ***
HousingStartGrowth.l2 0.0022799 0.0008132 2.804 0.00537 **
const 0.0264010 0.0121788 2.168 0.03092 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1948 on 316 degrees of freedom
Multiple R-Squared: 0.8889, Adjusted R-squared: 0.8875
F-statistic: 632.4 on 4 and 316 DF, p-value: < 2.2e-16
Estimation results for equation HousingStartGrowth:
===================================================
HousingStartGrowth = PriceIndexGrowthSA.l1 + HousingStartGrowth.l1 + PriceIndexGrowthSA.l2 + HousingStartGrowth.l2 + const
Estimate Std. Error t value Pr(>|t|)
PriceIndexGrowthSA.l1 -3.19814 3.46590 -0.923 0.3568
HousingStartGrowth.l1 0.14331 0.05587 2.565 0.0108 *
PriceIndexGrowthSA.l2 3.54160 3.46150 1.023 0.3070
HousingStartGrowth.l2 0.02817 0.05587 0.504 0.6145
const 0.39283 0.83667 0.470 0.6390
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 13.38 on 316 degrees of freedom
Multiple R-Squared: 0.02706, Adjusted R-squared: 0.01474
F-statistic: 2.197 on 4 and 316 DF, p-value: 0.06918
Covariance matrix of residuals:
PriceIndexGrowthSA HousingStartGrowth
PriceIndexGrowthSA 0.03794 -0.1165
HousingStartGrowth -0.11654 179.0462
Correlation matrix of residuals:
PriceIndexGrowthSA HousingStartGrowth
PriceIndexGrowthSA 1.00000 -0.04471
HousingStartGrowth -0.04471 1.00000Interpreting a VAR
Q: Can you interpret the number from the first table on variable HousingStartGrowth.l1?
A:
- Notice that there are 2 “regression” tables. That’s because we have a system of two equations.
- The parameter on HousingStartGrowth.l2 is 0.0022832
- This means that a one unit increase in the housing starts growth rate this month is associated with a 0.0022832 unit increase in housing prices in two months from now
- i.e. supply of homes is associated with future price increases (e.g. Say’s law, supply breeds demand???)
Q: Comment on the model’s ability to explain housing prices.
A:
- We’ll view the second output table
- Most of the coefficients are not statistically significant. The R2 is low and the F stat is above 5%.
- The implication is that after controlling for the simultaneity of prices, explaining housing is driven only by its own temporal dynamics (witness only HousingStartGrowth.l1 is significant)
- Note: that does NOT mean that the model is perfect. We could/should consider other features and model orders.
VAR Diagnostics
tsdisplay(VAR_est$varresult$PriceIndexGrowthSA$residuals, main = "Residuals of Price Index Growth")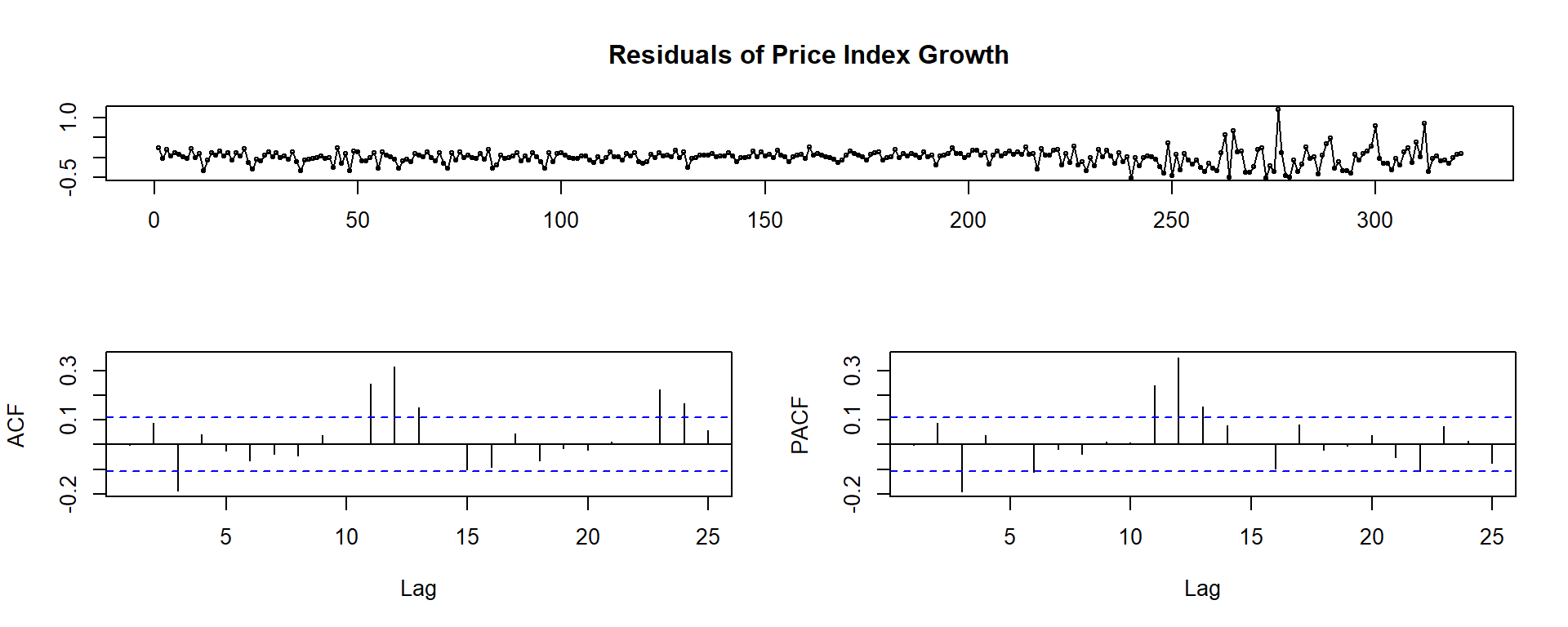
tsdisplay(VAR_est$varresult$HousingStartGrowth$residuals, main = "Residuals of Housing Start Growth")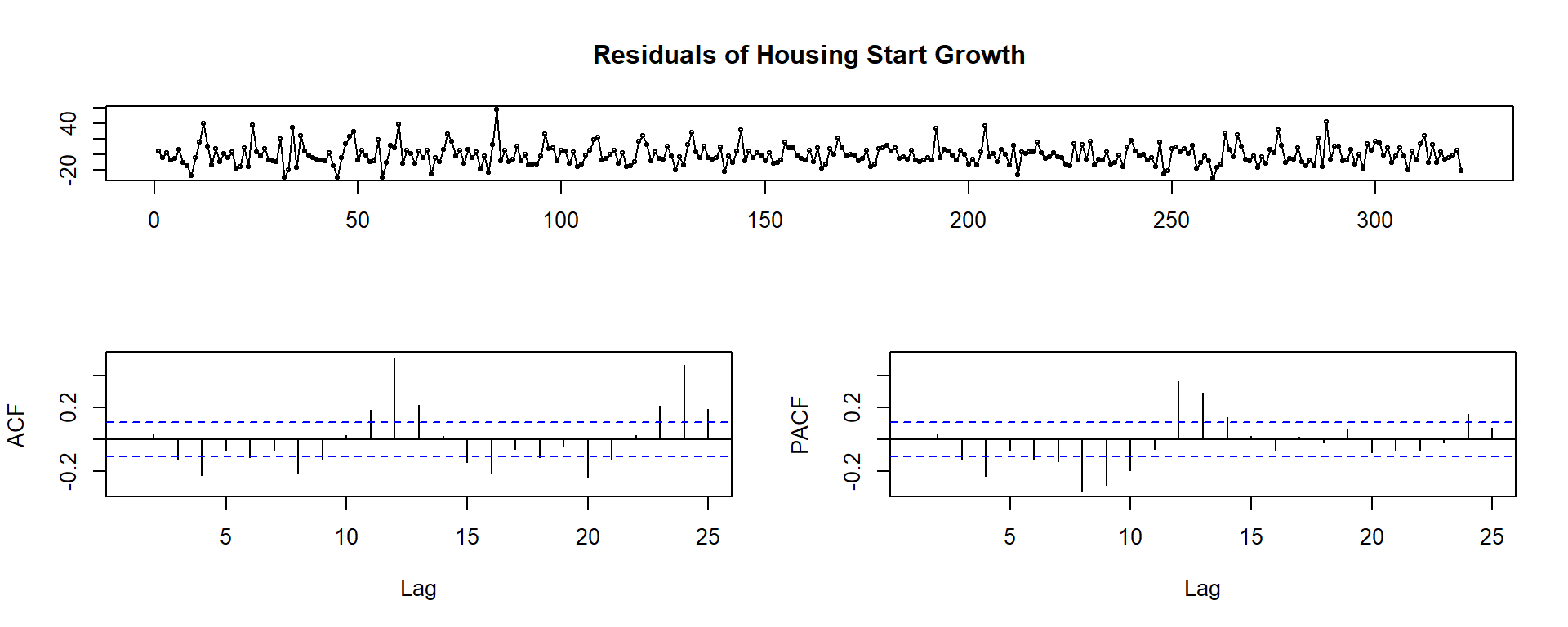
Q: Comments on the diagnostic graphs above.
A:
- Some annual seasonality seems to remain in each series, which you can see in the (P)ACF spikes near 12
- The model shows particular trouble modeling prices around COVID.
- Housing starts are worse in general (larger residuals than prices), but nothing unique about the COVID period
Fit Seasonal VAR
We can attempt to address that possible remaining seasonality with a seasonal VAR.
VAR_est2 <- VAR(y = VAR_data, p = 2, season = 12,type = "const")
summary(VAR_est2)
VAR Estimation Results:
=========================
Endogenous variables: PriceIndexGrowthSA, HousingStartGrowth
Deterministic variables: const
Sample size: 321
Log Likelihood: -1048.663
Roots of the characteristic polynomial:
0.8254 0.4468 0.3949 0.3949
Call:
VAR(y = VAR_data, p = 2, type = "const", season = 12L)
Estimation results for equation PriceIndexGrowthSA:
===================================================
PriceIndexGrowthSA = PriceIndexGrowthSA.l1 + HousingStartGrowth.l1 + PriceIndexGrowthSA.l2 + HousingStartGrowth.l2 + const + sd1 + sd2 + sd3 + sd4 + sd5 + sd6 + sd7 + sd8 + sd9 + sd10 + sd11
Estimate Std. Error t value Pr(>|t|)
PriceIndexGrowthSA.l1 1.285721 0.051557 24.938 < 2e-16 ***
HousingStartGrowth.l1 0.002664 0.001341 1.987 0.04779 *
PriceIndexGrowthSA.l2 -0.387471 0.051456 -7.530 5.77e-13 ***
HousingStartGrowth.l2 0.003741 0.001354 2.763 0.00607 **
const 0.025073 0.012283 2.041 0.04208 *
sd1 -0.097092 0.056781 -1.710 0.08829 .
sd2 -0.139247 0.064932 -2.145 0.03278 *
sd3 -0.126648 0.087339 -1.450 0.14806
sd4 -0.169836 0.091944 -1.847 0.06569 .
sd5 -0.114809 0.072249 -1.589 0.11308
sd6 -0.092868 0.066271 -1.401 0.16213
sd7 -0.085597 0.061595 -1.390 0.16564
sd8 -0.096589 0.059423 -1.625 0.10510
sd9 -0.081035 0.059830 -1.354 0.17661
sd10 -0.077289 0.061362 -1.260 0.20880
sd11 -0.037481 0.058301 -0.643 0.52078
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1961 on 305 degrees of freedom
Multiple R-Squared: 0.8913, Adjusted R-squared: 0.886
F-statistic: 166.8 on 15 and 305 DF, p-value: < 2.2e-16
Estimation results for equation HousingStartGrowth:
===================================================
HousingStartGrowth = PriceIndexGrowthSA.l1 + HousingStartGrowth.l1 + PriceIndexGrowthSA.l2 + HousingStartGrowth.l2 + const + sd1 + sd2 + sd3 + sd4 + sd5 + sd6 + sd7 + sd8 + sd9 + sd10 + sd11
Estimate Std. Error t value Pr(>|t|)
PriceIndexGrowthSA.l1 0.27874 2.16992 0.128 0.897872
HousingStartGrowth.l1 -0.40217 0.05643 -7.127 7.43e-12 ***
PriceIndexGrowthSA.l2 1.25750 2.16564 0.581 0.561899
HousingStartGrowth.l2 -0.16056 0.05698 -2.818 0.005149 **
const 0.70213 0.51696 1.358 0.175410
sd1 12.01711 2.38976 5.029 8.45e-07 ***
sd2 38.12833 2.73282 13.952 < 2e-16 ***
sd3 31.31043 3.67587 8.518 7.56e-16 ***
sd4 22.63547 3.86972 5.849 1.27e-08 ***
sd5 14.72165 3.04079 4.841 2.05e-06 ***
sd6 7.26714 2.78917 2.605 0.009624 **
sd7 6.27777 2.59239 2.422 0.016035 *
sd8 4.91925 2.50096 1.967 0.050096 .
sd9 9.13785 2.51811 3.629 0.000334 ***
sd10 -5.44807 2.58258 -2.110 0.035712 *
sd11 -9.10505 2.45373 -3.711 0.000246 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.254 on 305 degrees of freedom
Multiple R-Squared: 0.6427, Adjusted R-squared: 0.6251
F-statistic: 36.57 on 15 and 305 DF, p-value: < 2.2e-16
Covariance matrix of residuals:
PriceIndexGrowthSA HousingStartGrowth
PriceIndexGrowthSA 0.03846 0.08835
HousingStartGrowth 0.08835 68.12598
Correlation matrix of residuals:
PriceIndexGrowthSA HousingStartGrowth
PriceIndexGrowthSA 1.00000 0.05458
HousingStartGrowth 0.05458 1.00000Q: Assess goodness of fit.
A:
- The model fits are much improved. Witness the higher R2 and F stats.
tsdisplay(VAR_est2$varresult$PriceIndexGrowthSA$residuals, main = "Residuals of Price Index Growth")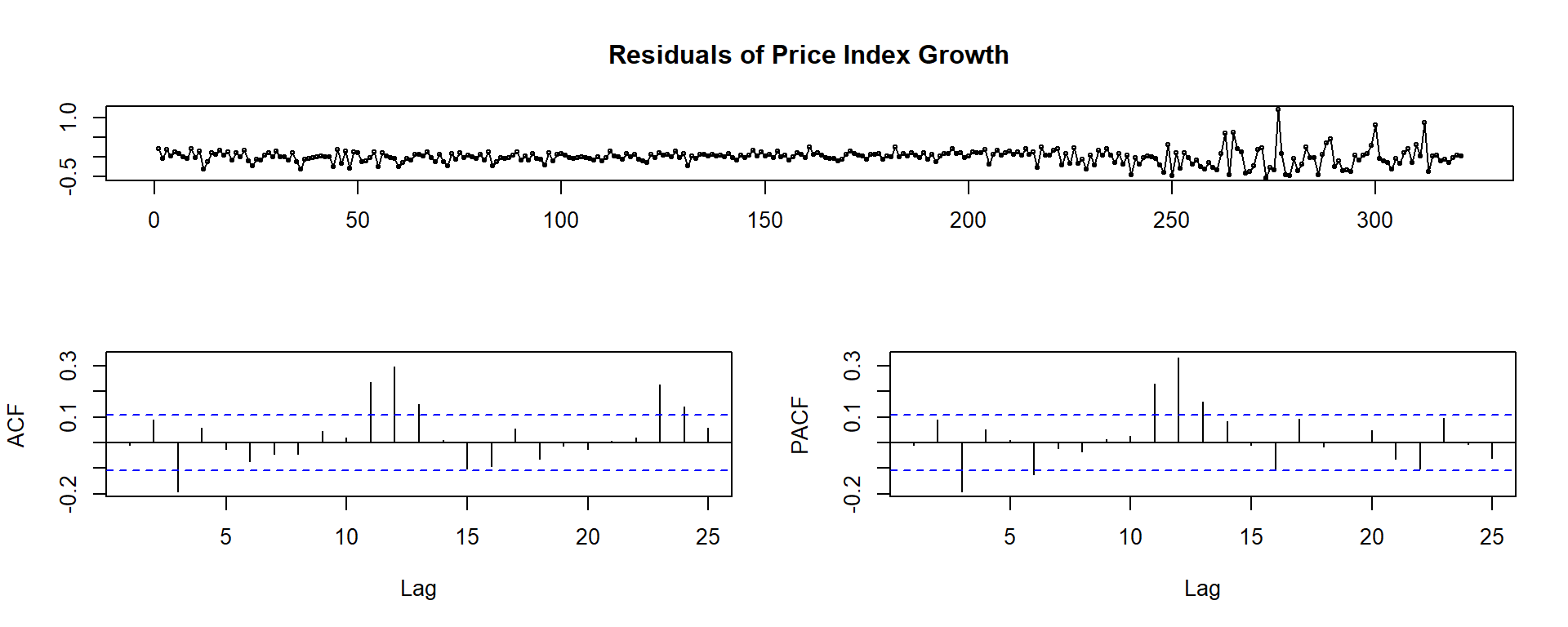
tsdisplay(VAR_est2$varresult$HousingStartGrowth$residuals, main = "Residuals of Housing Start Growth")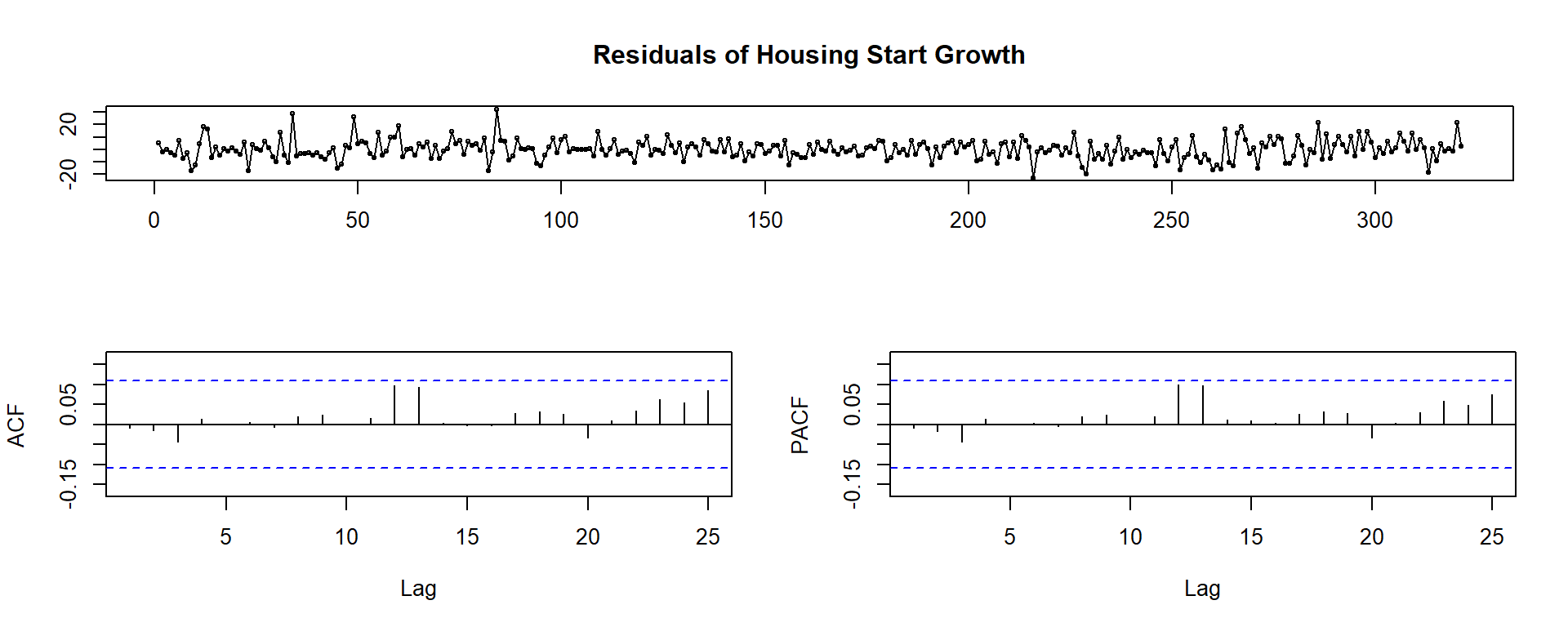
Q: Is the excess seasonality gone?
A:
- Appears to be gone for housing starts, but not prices.
- Again, prices are plagued by COVID. We should attempt to model that feature directly. Ignoring it could impact all of our estimates. We will avoid that for the sake of this tutorial.
Recall the impact of possible serial correlation. So, it’s best practice to consider our robust standard errors.
library(lmtest)
library(sandwich)
coeftest(VAR_est2, vcov. = sandwich)
t test of coefficients:
Estimate Std. Error t value
PriceIndexGrowthSA:(Intercept) 0.0250733 0.0161286 1.5546
PriceIndexGrowthSA:PriceIndexGrowthSA.l1 1.2857212 0.0744090 17.2791
PriceIndexGrowthSA:HousingStartGrowth.l1 0.0026642 0.0013822 1.9275
PriceIndexGrowthSA:PriceIndexGrowthSA.l2 -0.3874712 0.0720240 -5.3797
PriceIndexGrowthSA:HousingStartGrowth.l2 0.0037409 0.0016236 2.3041
PriceIndexGrowthSA:sd1 -0.0970923 0.0553261 -1.7549
PriceIndexGrowthSA:sd2 -0.1392470 0.0824081 -1.6897
PriceIndexGrowthSA:sd3 -0.1266483 0.0926315 -1.3672
PriceIndexGrowthSA:sd4 -0.1698356 0.0969567 -1.7517
PriceIndexGrowthSA:sd5 -0.1148091 0.0723592 -1.5867
PriceIndexGrowthSA:sd6 -0.0928683 0.0581576 -1.5968
PriceIndexGrowthSA:sd7 -0.0855970 0.0566814 -1.5101
PriceIndexGrowthSA:sd8 -0.0965894 0.0544240 -1.7748
PriceIndexGrowthSA:sd9 -0.0810346 0.0511425 -1.5845
PriceIndexGrowthSA:sd10 -0.0772885 0.0554792 -1.3931
PriceIndexGrowthSA:sd11 -0.0374806 0.0579890 -0.6463
HousingStartGrowth:(Intercept) 0.7021252 0.5785059 1.2137
HousingStartGrowth:PriceIndexGrowthSA.l1 0.2787415 2.4753603 0.1126
HousingStartGrowth:HousingStartGrowth.l1 -0.4021690 0.0566197 -7.1030
HousingStartGrowth:PriceIndexGrowthSA.l2 1.2574975 2.3858858 0.5271
HousingStartGrowth:HousingStartGrowth.l2 -0.1605623 0.0648896 -2.4744
HousingStartGrowth:sd1 12.0171122 2.7441907 4.3791
HousingStartGrowth:sd2 38.1283288 3.4915029 10.9203
HousingStartGrowth:sd3 31.3104346 3.9627555 7.9012
HousingStartGrowth:sd4 22.6354672 4.1176580 5.4972
HousingStartGrowth:sd5 14.7216498 3.3386120 4.4095
HousingStartGrowth:sd6 7.2671352 2.8217251 2.5754
HousingStartGrowth:sd7 6.2777745 2.7815203 2.2570
HousingStartGrowth:sd8 4.9192467 2.7364834 1.7977
HousingStartGrowth:sd9 9.1378540 2.8416767 3.2157
HousingStartGrowth:sd10 -5.4480716 2.7868616 -1.9549
HousingStartGrowth:sd11 -9.1050479 2.8829044 -3.1583
Pr(>|t|)
PriceIndexGrowthSA:(Intercept) 0.121082
PriceIndexGrowthSA:PriceIndexGrowthSA.l1 < 2.2e-16 ***
PriceIndexGrowthSA:HousingStartGrowth.l1 0.054842 .
PriceIndexGrowthSA:PriceIndexGrowthSA.l2 1.488e-07 ***
PriceIndexGrowthSA:HousingStartGrowth.l2 0.021889 *
PriceIndexGrowthSA:sd1 0.080279 .
PriceIndexGrowthSA:sd2 0.092102 .
PriceIndexGrowthSA:sd3 0.172561
PriceIndexGrowthSA:sd4 0.080837 .
PriceIndexGrowthSA:sd5 0.113627
PriceIndexGrowthSA:sd6 0.111337
PriceIndexGrowthSA:sd7 0.132042
PriceIndexGrowthSA:sd8 0.076935 .
PriceIndexGrowthSA:sd9 0.114119
PriceIndexGrowthSA:sd10 0.164601
PriceIndexGrowthSA:sd11 0.518546
HousingStartGrowth:(Intercept) 0.225806
HousingStartGrowth:PriceIndexGrowthSA.l1 0.910417
HousingStartGrowth:HousingStartGrowth.l1 8.645e-12 ***
HousingStartGrowth:PriceIndexGrowthSA.l2 0.598537
HousingStartGrowth:HousingStartGrowth.l2 0.013890 *
HousingStartGrowth:sd1 1.640e-05 ***
HousingStartGrowth:sd2 < 2.2e-16 ***
HousingStartGrowth:sd3 5.064e-14 ***
HousingStartGrowth:sd4 8.163e-08 ***
HousingStartGrowth:sd5 1.438e-05 ***
HousingStartGrowth:sd6 0.010483 *
HousingStartGrowth:sd7 0.024718 *
HousingStartGrowth:sd8 0.073221 .
HousingStartGrowth:sd9 0.001441 **
HousingStartGrowth:sd10 0.051507 .
HousingStartGrowth:sd11 0.001746 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Q: Where is seasonality more significant (prices or starts)?
A:
- After controlling for the dynamic interactions, it appears that seasonality is more apparent in the housing starts model.
- Witness the bottom half of the table, coefficients such as HousingStartGrowth:sd1 have low pvalues indicating a significant seasonal difference.
- The pvalues from the coefficients above suggest some indication of today’s housing starts to explain tomorrow’s prices, but not vice versa.
- We need a test of combine the aggregated effects of these forces.
Determining Direction of causality
If Housing Starts today have an impact on Prices tomorrow, then Housing Starts are said to Granger Cause Prices.
causality(VAR_est2, cause = "HousingStartGrowth")$Granger
Granger causality H0: HousingStartGrowth do not Granger-cause
PriceIndexGrowthSA
data: VAR object VAR_est2
F-Test = 4.4204, df1 = 2, df2 = 610, p-value = 0.01242Q: Interpret the test.
A: Given the low pvalue we reject the null, suggesting that housing starts have a leading impact on prices.
Let’s examine the other direction.
causality(VAR_est2, cause = "PriceIndexGrowthSA")$Granger
Granger causality H0: PriceIndexGrowthSA do not Granger-cause
HousingStartGrowth
data: VAR object VAR_est2
F-Test = 1.798, df1 = 2, df2 = 610, p-value = 0.1665Q: Interpret the test.
A:
- The relatively high pvalue suggests that we fail to reject.
- Prices don’t “cause” starts
- The causal direction is only one way (housing starts to prices).
Impulse Response Function (IRF)
Another way to understand and use the VAR estimates is via a stress test. For instance, what happens to Prices over the next 2yrs if we get a shock to housing starts today?
irf_PriceIndexGrowth <- irf(VAR_est2, impulse = "HousingStartGrowth",
response = "PriceIndexGrowthSA",
cumulative = FALSE,
n.ahead = 20, boot = TRUE)
irf_PriceIndexGrowth$irf$HousingStartGrowth[3][1] 0.05023096plot(irf_PriceIndexGrowth, ylab = "Price Index Growth", main = "Cumulative Impact of 1 sigma shock to Housing Starts")
irf_PriceIndexGrowth <- irf(VAR_est2, impulse = "HousingStartGrowth",
response = "PriceIndexGrowthSA",
cumulative = TRUE,
n.ahead = 20, boot = TRUE)
irf_PriceIndexGrowth$irf$HousingStartGrowth[3][1] 0.0721883plot(irf_PriceIndexGrowth, ylab = "Price Index Growth", main = "Cumulative Impact of 1 sigma shock to Housing Starts")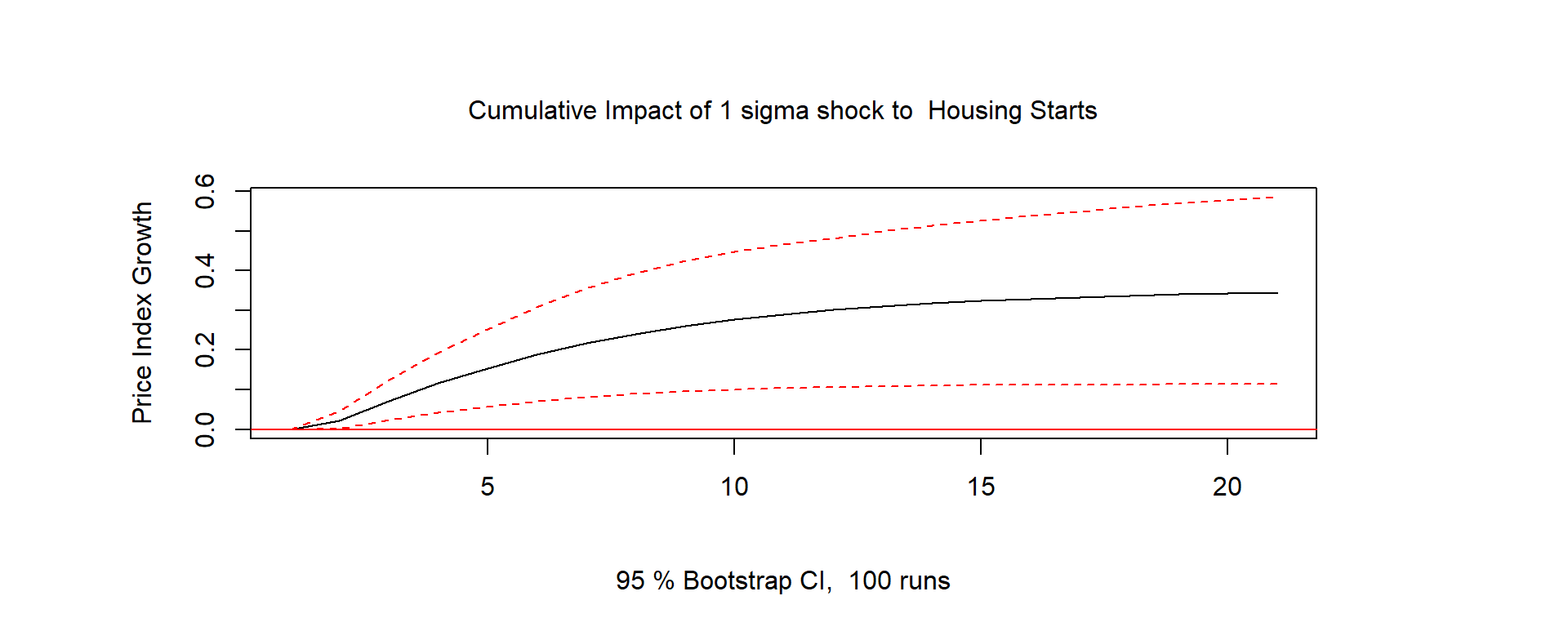
Q: How do we interpret the IRF?
A:
- From the first graph we can see that a 1 sigma rise in housing starts this month will trigger a rise in house price growth next month
- This shock’s effect will grow more in the second and third months.
- By the 4th and 5th months, the shock’s impact is fading.
- Within roughly 1.5-2 yrs, the shock’s impact is gone.
- The second graph shows the CUMULATIVE impacts, which tells the same story, but from a different visual perspective.
irf_HousingStartGrowth <- irf(VAR_est2, impulse = "PriceIndexGrowthSA",
cumulative = FALSE,
response = "HousingStartGrowth",
n.ahead = 20, boot = TRUE)
plot(irf_HousingStartGrowth, ylab = "Housing Start Growth", main = "Cumulative Impact from 1 sigma shock to Prices")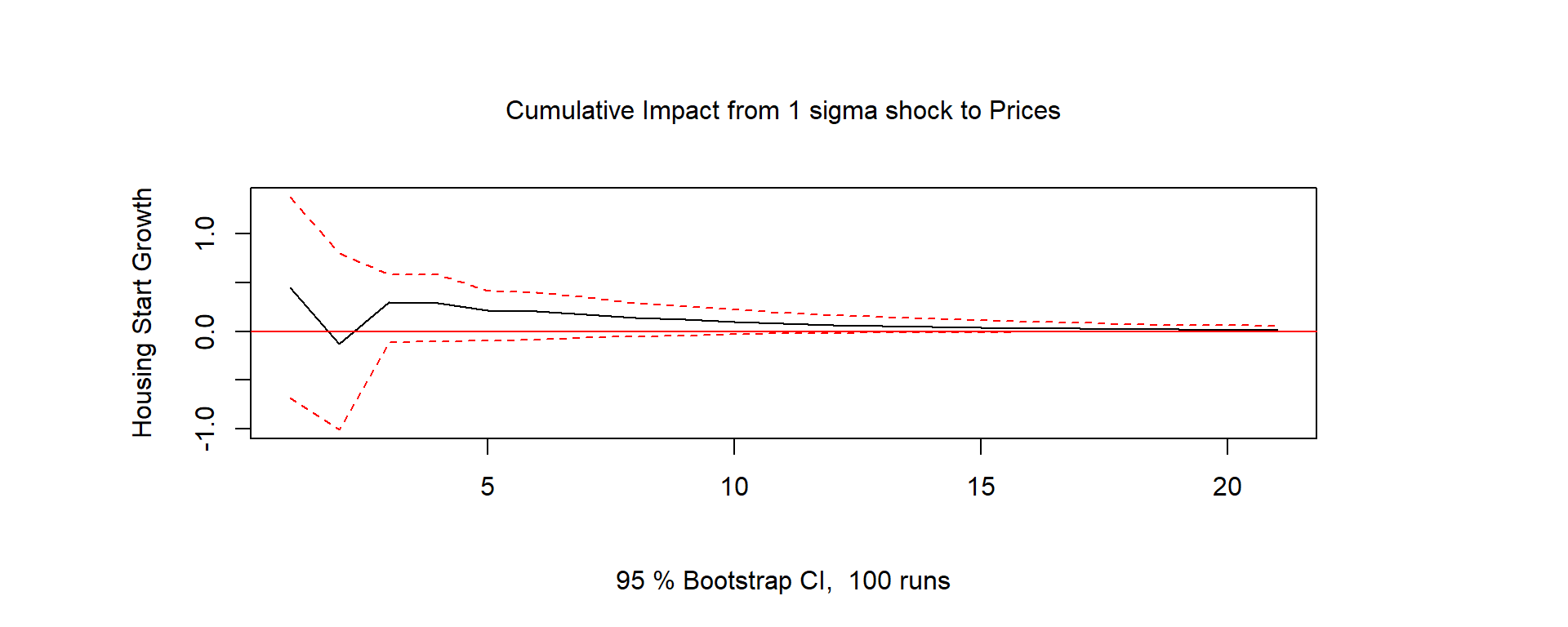
irf_HousingStartGrowth <- irf(VAR_est2, impulse = "PriceIndexGrowthSA",
cumulative = TRUE,
response = "HousingStartGrowth",
n.ahead = 20, boot = TRUE)
plot(irf_HousingStartGrowth, ylab = "Housing Start Growth", main = "Cumulative Impact from 1 sigma shock to Prices")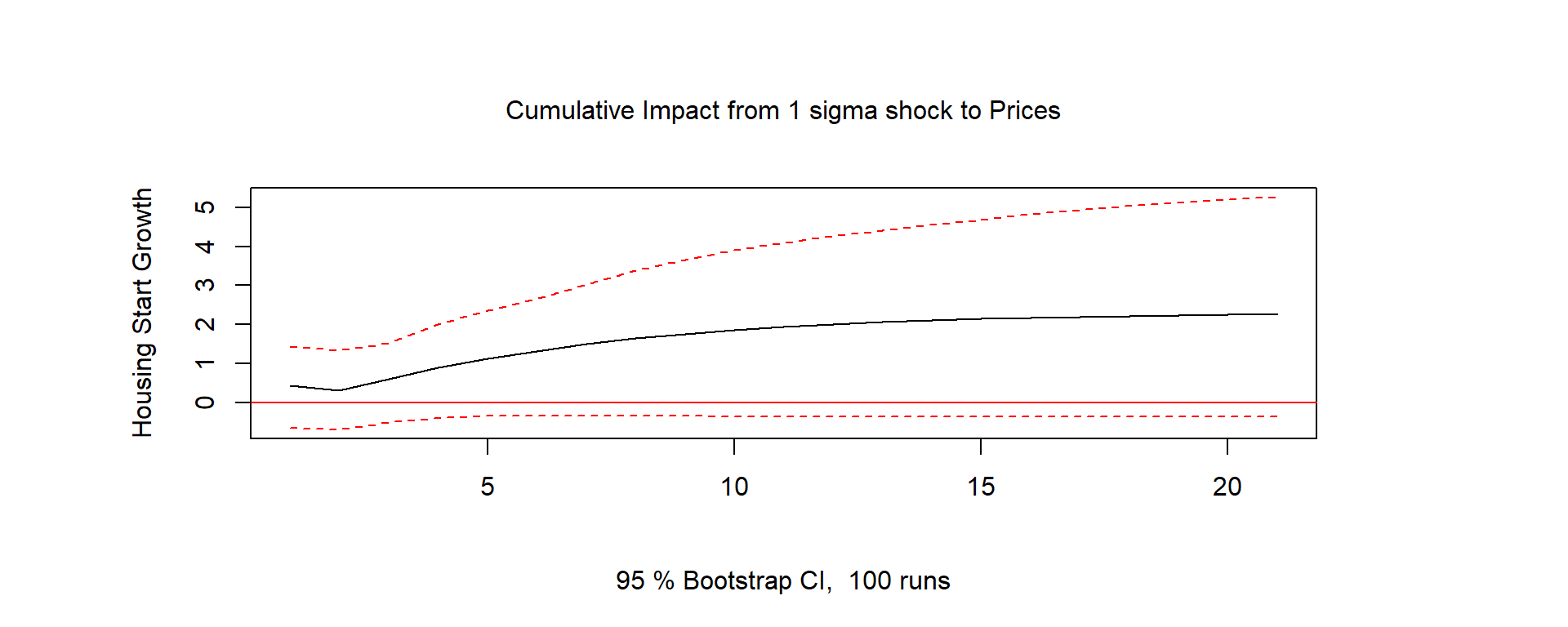
Q: Interpret the IRF
A:
- A one unit increase in prices triggers a drop in housing starts for a couple of months
- Then the impact rises and fades quickly
- Notice that throughout the CI bands in red surround the 0 line, indicating little statistical significance.
Forecast with VAR
Given the causality findings, we may consider refining the model. For now, we’ll use that estimated structure to predict both Prices and Starts 24-months head.
VAR_mulpred <- predict(VAR_est2, n.ahead = 24)
plot(VAR_mulpred, names = "PriceIndexGrowthSA", main = "Forecast of Price Growth")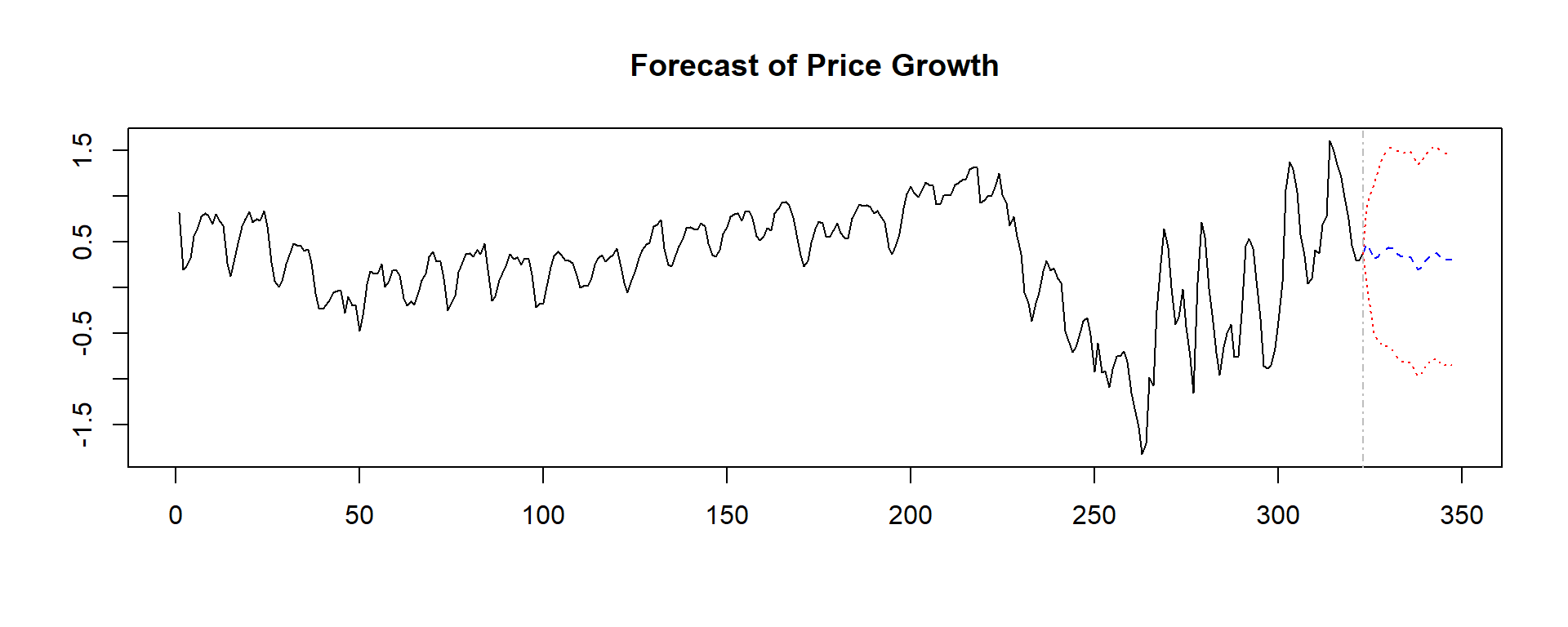
plot(VAR_mulpred, names = "HousingStartGrowth", main = "Forecast of Housing Starts Growth")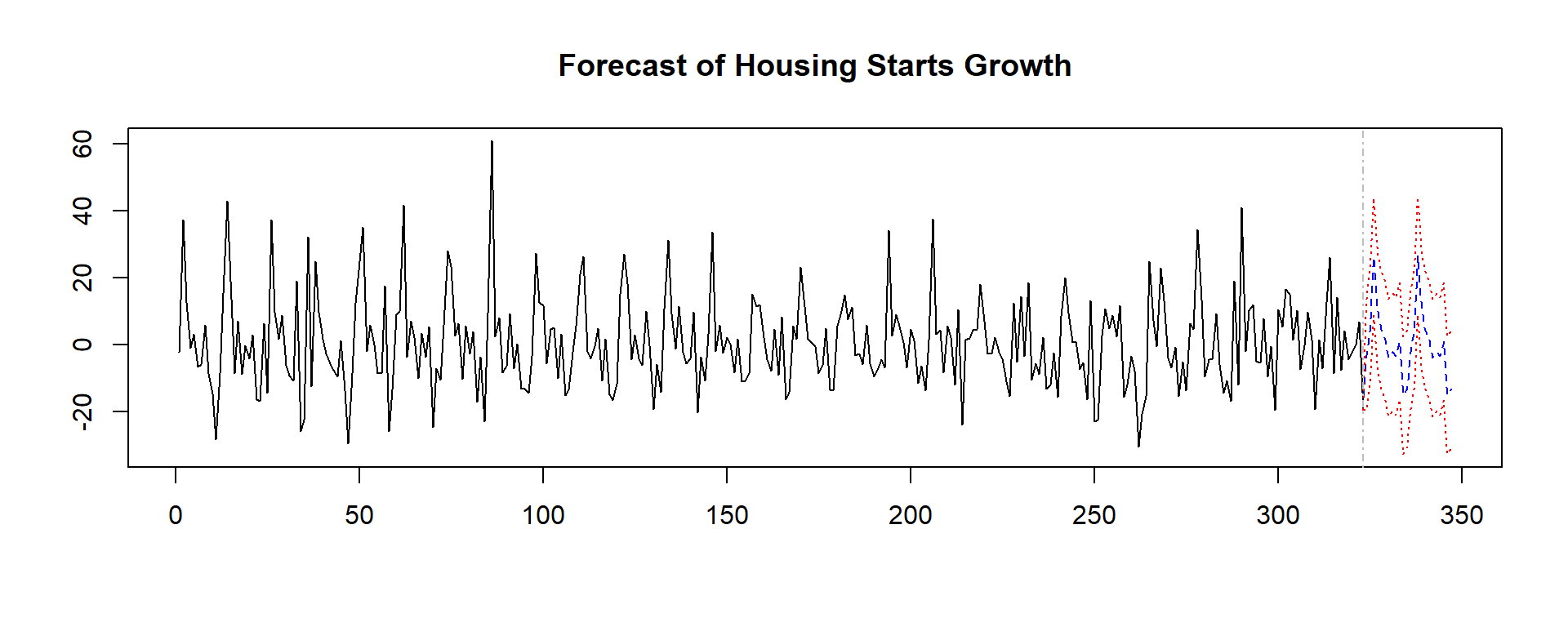
Q: What do the red dashed lines in the two graphs signify. Comment on their differences.
A:
- The red dashed lines are 95% CIs.
- The Price Growth CIs are very wide. We saw evidence of this earlier with the poor explanatory power especially during COVID.
- Meanwhile, the housing starts forecast seems much more stable.
- It detects the seasonality and accommodates the dynamic linkages with prices.